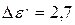В ионных кристаллах при приложении внешнего электрического поля наряду с электронно-деформационной поляризацией происходит смещение ионов и анионов по- и против направления поля. Одновременно с этим на них действует сила упругого смещения, и заряды совершают колебательные движения около положения равновесия. Разность фаз колебаний ионов приводит к возникновению поляризации диэлектрика. Для получения формулы, позволяющей рассчитать величину диэлектрической проницаемости ионных кристаллов, рассмотрим модель одномерной цепочки состоящей из периодически расположенных атомов. В качестве примера возьмем цепочку, из атомов натрия и хлора, реализуемую в кристаллах хлорида натрия.
Рис.
Пронумеруем все ионы и анионы, входящие в цепочку атомов. Анионы хлора обозначим, как четные Cl - - 2n (n=1,2,3,4...), а ионы натрия, как нечетные Na+1
- 2n+1 (n=1,2,3,4...). Массу анионов хлора обозначим - М, а массу ионов натрия - m.
Движение атомов под действием внешнего электрического поля будет определяться уравнениями:
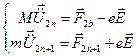, (30)
где F2n и F2n+1 сила упругой связи атомов хлора и натрия; U2n и U2n+1 смещение атомов под действием внешнего электрического поля Е.
Если учесть, что под действием внешнего электрического поля действующего по одной оси смещаются как четные, так и нечетные атомы друг относительно друга, то силы упругой связи катионов и анионов будут определяться соотношением:
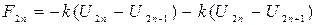
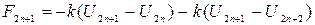, (31)
где k – коэффициент упругой связи атомов.
С учетом соотношений (30) и (31) систему уравнений можно представить в виде:
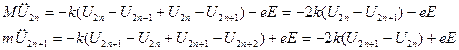, (32)
Решениями полученных дифференциальных уравнений являются соотношения, описывающие изменение смещения атомов под действием поля:
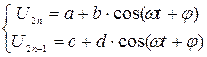, (33)
где φ – разность фаз колебаний; ω – частота внешнего электрического поля; a – начальное смещение четных атомов; c – начальное смещение нечетных атомов; b и d – амплитуды колебаний четных и нечетных атомов.
Подставим данные решения (33) и их производные в уравнения (32) и получим:
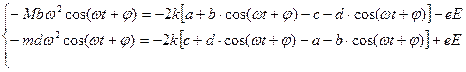, (34)
Для решения системы уравнений приравняем друг другу члены, содержащие косинусы и свободные члены:
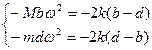, (35) 
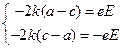, (36)
Составим главный определитель системы уравнений (35) и прировняем его нулю:
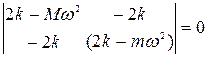, (37)
Решение этой системы уравнений приводит к дисперсионному уравнению: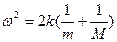 
. (38)
Из решения второй системы уравнений (36) можно найти разность постоянных смещений нечетных атомов относительно четных:
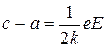, (39)
Зная постоянные смещения атомов друг относительно друга (39) можно найти постоянный электрический момент р.
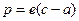, (40)
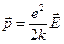, (41)
Общую поляризацию диэлектрика можно получить из соотношений (15) и (41):
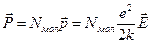, (42)
где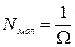 
и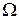 
- объем одной молекулы.
Подставим в соотношение (42) вместо коэффициента упругой связи его выражение, полученное путем преобразования дисперсионного уравнения (38):
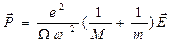, (43)
Сопоставляя (43) с соотношением (8) получим формулу, определяющую величину диэлектрической проницаемости для ионных кристаллов:
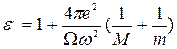, (44)
Добавка к величине диэлектрической проницаемости в ионных кристаллах, обусловленная ионно-деформационной поляризацией рассчитывается по формуле Борна:
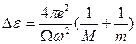, (45)
Для кристаллов хлористого натрия она составляет 
