Цель работы: изучение последовательного, параллельного и смешанного соединений сопротивлений; экспериментальная проверка законов Ома, Кирхгофа и баланса мощностей.
Основные теоретические положения
В данной работе исследуется электрическая цепь, состоящая из трех резисторов при их последовательном, параллельном и смешанном соединениях.
При последовательном соединении сопротивлений (рис. 2.1, а) общее сопротивление цепи равно сумме сопротивлений, входящих в состав цепи, т. е.
.
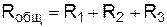При параллельном соединении сопротивлений (рис. 2.1, б) общая проводимость цепи равна сумме проводимостей отдельных ее ветвей:
,
где 
– проводимость соответствующего участка электрической цепи, См (Сименс).
При смешанном соединении сопротивлений (рис. 2.1, в) общее сопротивление цепи определяется как сумма сопротивлений последовательного и параллельного участков цепи:
,
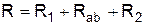где 
; 
.
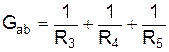а б в
Рис. 2.1. Электрические цепи соединения сопротивлений: а – последовательное;
б – параллельное; в – смешанное
Закон Ома устанавливает связь между током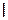 
и напряжением 
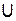на некотором участке цепи. Ток в проводнике прямо пропорционален напряжению между концами проводника и обратно пропорционален сопротивлению этого же проводника, т. е. 
.
1-й закон Кирхгофа. Алгебраическая сумма токов, подтекающих к любому узлу разветвленной электрической цепи, равна нулю 
, или сумма подтекающих к любому узлу токов равна сумме оттекающих от узла токов (рис. 2.1, б): 
, или 
.
2-й закон. Алгебраическая сумма падений напряжений в любом замкнутом контуре электрической цепи равна алгебраической сумме эдс вдоль того же контура (рис. 2.1, а), т. е. 
, или алгебраическая сумма напряжений (не падений напряжений) вдоль любого замкнутого контура равна нулю, т. е. 
: 
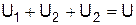, или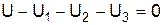 
.
Закон Джоуля–Ленца устанавливает связь между энергией, выделяемой в сопротивлении нагрузки, и током, проходящим через него:
, при 
; 
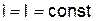, Дж;
, Вт, – мощность нагрузки.
Баланс мощностей (закон сохранения энергии в электрической цепи). Суммарная мощность источников электрической энергии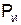 
равна общей мощности, поглощаемой сопротивлениями нагрузки (потребителями) 
, входящими в состав цепи, т. е.
= 
.
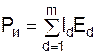Относительная ошибка 
должна быть меньше наперед заданного числа, например 5 %:
.
Порядок выполнения работы
1. Собрать схему (рис. 2.2). Измерить напряжение на каждом сопротивлении и на входе цепи. Записать показание амперметра. Вычислить сопротивление каждого участка и всей цепи. Рассчитать мощность, потребляемую каждым сопротивлением. Измеренные и вычисленные значения занести в первую строку табл. 2.1. Убедиться, что 
, 
, 
.
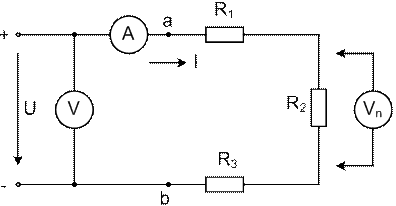
Рис. 2.2. Схема неразветвленной цепи при последовательном соединении сопротивлений
2. Собрать схему (рис. 2.3). Измерить напряжение и общий ток. Зная из предыдущего опыта значения сопротивлени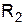й 
, 
и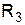 
, определить проводимости ветвей, токи в каждой ветви и мощность на каждом участке цепи. Результаты измерений и вычислений занести во вторую строку табл. 2.1. Убедиться, что 
, 
, .
Рис. 2.3. Схема разветвленной цепи при параллельном соединении сопротивлений
3. Собрать схему (рис. 2.4). Измерить ток и напряжение на каждом сопротивлении и во всей цепи. Рассчитать ток и мощность в каждой ветви. Результаты измерений и расчетов занести в третью строку табл. 2.1. Убедиться, что 
, 
, 
, .
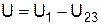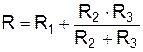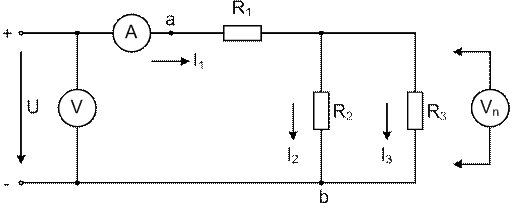
Рис. 2.4. Схема разветвленной цепи при смешанном соединении сопротивлений
Таблица 2.1
