1. Содержание пункта начинается с рассмотрения примера последовательности натуральных чисел, которые при делении на 4 дают в остатке 1, что позволяет ввести два понятия: арифметической прогрессии и разности арифметической прогрессии (числа d). Каждому из этих понятий дается определение, причем определение арифметической прогрессии представлено в двух формах: 1) в виде словесной формулировки (арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом), 2) в виде аналитической записи (арифметическая прогрессия — последовательность, заданная формулой 
, где d — некоторое число).
2.В пункте рассматриваются и доказываются два утверждения:
1) формула n-го члена арифметической прогрессии (
);
2) каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов.
Этим объясняется название «арифметическая прогрессия».
Формула n-го члена выводится индуктивно, на основании обобщения вида записи первых четырех членов некоторой арифметической прогрессии. Идея доказательства прямого утверждения о задании арифметической прогрессии формулой вида 
заключается в преобразовании формулы n-го члена арифметической прогрессии к виду 
. Для доказательства обратного утверждения находят разность (п + 1)-го и п- гочленов последовательности (
)и показывают, что эта разность является постоянным числом, значит,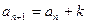 
, отсюда делается вывод, что последовательность ()является арифметической прогрессией с разностью d.
3. В объяснительном тексте пункта рассмотрены задания,которые решаются по определению или по формуле п- гочлена арифметической прогрессии.
а) Примеры нахождения нескольких членов арифметической прогрессии (ап), если известны 
и d, которые позволяют усвоить определение арифметической прогрессии и рассмотреть ее случаи, когда и d являются натуральными, целыми отрицательными числами; рассмотрен случай, когда d = 0.
б) Задача на вычисление п- гочлена арифметической прогрессии (ап), если известны и d этой прогрессии, которая демонстрирует вычисления по формуле n-го члена.
в) Задание на определение того, является ли данное число прогрессии (хп), для которой указаны несколько первых членов. Алгоритма выполнения задания в пункте не дается, но последовательность действий можно выделить.
г) На нахождение формулы n-го члена по заданным некоторым членам.
д) геометрического содержания на доказательство.
II. Проведем анализ задачного материала пункта. Все задачи пункта условно можно разделить на 5 групп, каждая из которых отрабатывает определенные умения.
1-я группа. Нахождение п- гочлена арифметической прогрессии:
По определению, если известны  и  (№ 234)
| По формуле n-го члена прогрессии, если известны и (№ 236)
| По формуле n-го члена прогрессии, если прогрессия задана перечисле-нием своих членов (№ 238, 239, 240) | По рядом стоящим членам |
В этих задачах рассматриваются всевозможные значения и , первый член как положительный, так и отрицательный; разность прогрессии тоже может быть как отрицательной, так и положительной. Такой подбор первых членов арифметической прогрессии и разности позволяет отработать понятия убывающей и возрастающей арифметической прогрессии.
2-я группа (обратная к 1-й группе).
Нахождение первого члена арифметической прогрессии (или разности), если известны:
| п-й член и d (№ 242, 243) | п-й член и a1 (№ 241) | Два любых члена прогрессии (№ 247, 237) |
В этих упражнениях решение сводится к составлению уравнения или системы двух уравнений с двумя неизвестными.
3-я группа (обратная к 1-й группе).
Нахождение номера члена арифметической прогрессии с целью:
| определения того, является ли заданное число членом данной арифметической прогрессии или нет (№ 239, 240), причем прогрессия может быть задана первыми двумя членами или и
| Указания номеров положительных или отрицательных членов прогрессии (№245, 246) |
4-я группа. Составление прогрессии:
| по заданному набору чисел (№ 237, 244) | По сюжетной задаче (№ 248, 249) |
Задачи № 241, 247даны с целью отработки умения нахождения нескольких членов арифметической прогрессии, стоящих между первым и п -мчленом прогрессии, т. е. умения по заданным а1 и ап находить d, используя формулу ап = а1 + d(n - 1), а затем по определению записывать несколько членов арифметической прогрессии.
В сюжетных задачах нужно определить, что рассматриваемый процесс (физический № 248, 249 или геометрический) в объяснении текста, можно задать арифметической прогрессией; определить ее первый член и разность, а затем n-й член прогрессии и дать ответ на поставленный вопрос задачи. Эти задания позволяют показать использование арифметической прогрессии в практической жизни.
5-я группа. Использование признака арифметической прогрессии: последовательность вида 
является арифметической прогрессией (№ 235).
В упражнении № 363 нужно по виду формулы общего члена последовательности (ап) установить, является ли последовательность арифметической прогрессией или нет, т. е. отрабатывается умение сравнить данную формулу с формулой , определения значений 
и 
.
III. Поурочное планирование (3 ч).
| № | Цели урока | Распределение материала | Контроль | |
| в классе | на дом | |||
| 1. | Ввести понятие арифметичес-кой прогрессии, научиться находить по определению члены прогрессии, если прогрессия задана первым членом и разностью или перечислением ее первых членов, вывести формулу п- гочлена, научиться находить по этой формуле члены прогрессии, если прогрессия задана первым членом и разностью или перечислением ее первых членов | 1. Примеры на «да» и «нет».
2. № 233
3. Дано: ар. пр.: -1, 1, 3, 5,... Найти: 
4. № 235
5. №238
| 1.Выучить определение и формулу п -го члена. 2. Привести примеры ар. пр. 3.№ 237, 240 | 1.Опрос в парах и обмен примерами, где «авторы» обосновывают свой выбор 2.№ 239, аналогичный домашнему |
| 2. | Проверить усвоение определения и формулы, научиться составлять и решать задачи, обратные рассмотренным на 1-м уроке, научиться работать с арифметической прогрессией, заданной двумя своими членами | № 239 аналогичный домашнему №243, №241, № 247, №237 | № 242, № 245, № 246 | Самостоятельная работа по обязательным результатам |
| 3. | Проверить обязательные результаты обучения, рас-смотреть составление ариф-метической прогрессии: а) по заданному набору чисел, б) по сюжетной задаче, научиться проверять, является ли последовательность, за-данная формулой п- гочлена, арифметической прогрессией | № 248 из дид. матер. | № 251, № 249 | Самостоятельная работа по обратным задачам, № 245 аналогичный домашнему |
Рекомендации по планированию и разработке уроков по математике
