Теплопередача через плоские, цилиндрические и сферические стенки при установившемся процессе

Рисунок 7.20 – Характер изменения температур при теплопередаче через плоскую стенку

Теплопередача через плоскую стенку. На рис. 7.20 показана плоская стенка толщиной , материал которой имеет коэффициент теплопроводности . По одну сторону стенки движется теплоноситель с температурой t ₁ (в ядре потока), по другую сторону – теплоноситель с температурой t ₂. Температуры поверхностей стенки и ; коэффициенты теплоотдачи и ; .

При установившемся процессе количество тепла, передаваемого в единицу времени через площадь F от ядра потока горячего теплоносителя к стенке, равно количеству тепла, передаваемого через стенку и от стенки к ядру потока холодного теплоносителя. Это количество тепла можно определить по любому из соотношений:

Из этих соотношений:

(7.167)

Сложив левые и правые части равенств (7.167), получим

либо

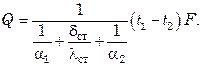(7.168)

Из сопоставления уравнений (7.165) и (7.168) следует, что

, (7.169)

или . (7.170)

Величина , обратная коэффициенту теплопередачи, носит название термического сопротивления теплопередаче. Величины 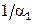и являются термическими сопротивлениями теплоотдаче, а – термическим сопротивлением стенки. Таким образом, термическое сопротивление теплопередаче равно сумме термических сопротивлений теплоотдаче и стенки, т.е. общее термическое сопротивление равно сумме частных. Поэтому, если стенка состоит из нескольких слоев толщиной 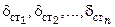и коэффициенты теплопроводности их соответственно равны то термическое сопротивление теплопередаче такой стенки

,

или . (7.171)

В этом случае выражение (7.169) для коэффициента теплопередачи K принимает следующий вид:

. (7.172)

Анализ уравнений (7.169) и (7.172) показывает, что коэффициент теплопередачи K зависит в основном от значения наибольшего из термических сопротивлений. Поэтому для интенсификации процесса теплообмена необходимо прежде всего уменьшить термическое сопротивление с той стороны, с которой оно является наибольшим.

Коэффициент теплопередачи всегда меньше любого из коэффициентов теплоотдачи и снижается с увеличением толщины стенки, уменьшением коэффициента ее теплопроводности, а также с увеличением толщины слоев отложений на ней.

Подставляя значение удельного теплового потока Q / F в уравнения (7.167), можно определить температуры стенки и :

(7.173)

 

Рисунок 7.21 – Теплопередача через цилиндрическую стенку

Теплопередача через цилиндрическую стенку. Внутри трубы длиной L с внутренним диаметром d ₁и внешним d ₂(рис. 7.21) протекает горячий теплоноситель с температурой t ₁. Снаружи труба омывается холодным теплоносителем с температурой t ₂. Стенка трубы однородна, и коэффициент ее теплопроводности равен ; температуры внутренней и наружной стенок трубы соответственно и . Температуры теплоносителей и стенки изменяются только в направлении радиуса. Со стороны горячего теплоносителя коэффициент теплоотдачи , а со стороны холодного – .

При установившемся процессе количества тепла, отданное горячим теплоносителем стенке, переданное через стенку и отданное стенкой холодному теплоносителю, равны. Следовательно,

(7.174)

Частные температурные напоры из уравнений (7.174):

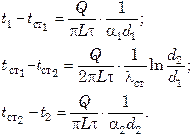(7.175)

Складывая уравнения системы (7.175), получим полный температурный напор:

, (7.176)

а тепловой поток

. (7.177)

Обычно при теплопередаче через цилиндрическую стенку определяют количество тепла, передаваемое через единицу длины трубы (L = 1), и уравнение теплопередачи представляют в виде

, (7.178)

где – линейный коэффициент теплопередачи (Вт/м·К), равный:

. (7.179)

Расчетные формулы теплопередачи через цилиндрические стенки довольно громоздки, поэтому при практических расчетах применяют некоторые упрощения. Так, для тонкостенных труб, пренебрегая кривизной стенки, используют для расчета уравнение для плоской стенки (7.168):

, (7.180)

где – коэффициент теплопередачи для плоской стенки; d _р – расчетный диаметр трубы; – толщина стенки трубы, равная .

Погрешность расчета при использовании уравнения (7.180) при 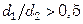не превышает 4 %.

В качестве расчетного диаметра d _р берут тот диаметр трубы, со стороны которого коэффициент теплоотдачи имеет меньшее значение. Если же значения коэффициентов теплоотдачи и одного порядка, то d _р принимают равным среднеарифметическому между внутренним d ₁ и внешним d ₂ диаметрами, т.е.:

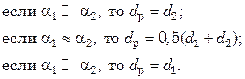
По аналогии с коэффициентом теплопередачи для многослойной плоской стенки коэффициент теплопередачи для многослойной цилиндрической стенки

. (7.181)

Рисунок 7.22 – Теплопередача через шаровую стенку

Аналогично определяют и температуры стенок и .

Теплопередача через шаровую стенку. Внутренний диаметр шара (рис. 7.22) равен d ₁, внешний – d ₂, коэффициент теплопроводности . Внутри шара находится горячий теплоноситель с температурой t ₁, снаружи – холодный теплоноситель с температурой t ₂. Значения коэффициентов теплоотдачи соответственно и . Температуры поверхности стенок и .

При установившемся режиме количество тепла (Вт), переданное от горячего теплоносителя к холодному через стенку, выразится уравнениями:

(7.182)

(7.183)

или ,

где K _ш – коэффициент теплопередачи для шаровой стенки (Вт/К), равный:

. (7.184)