Показателей дохода и издержек. показателей дохода и издержек.
Максимизация прибыли, Максимизация прибыли,
Минимизация убытков и случай минимизация убытков и случай
Закрытия закрытия
Задача 2. Предприятие производит продукцию по цене 250тыс. руб. за единицу. Средние переменные издержки составляют при этом 200тыс. руб. Общие постоянные расходы 500тыс. руб. В результате роста арендной платы расходы увеличились на 10%. Как изменится критический объем?
Решение. Критический объем производства – это минимальный объем, при котором достигается безубыточное производство. Увеличение производства сверх этого объема ведет к получению прибыли. Определение критического объема предполагает, что цена за единицу продукции и средние переменные издержки остаются неизменными. Критический объем рассчитывается по формуле: T=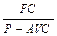 
, где:
T – критический объем производства;
FC – постоянные издержки;
AVC – средние переменные издержки;
P – цена.
T 1 = 
= 
= 
=10 ед.
При увеличении арендной платы на 10% постоянные расходы FC составят 550тыс. руб. Если цена и средние переменные издержки не изменились, то возмещение возросших постоянных издержек произойдет при увеличении производства.
T 2 = = 
= 
=11ед.
Критический объем увеличивается.
Задача 3. В отрасли действует 30 фирм. Общие издержки каждой фирмы равны TC = q3 – 6q2 + 18q. Функция спроса имеет вид Qd = 180-3P, где P – цена товара. Определите равновесную цену и объем спроса в долгосрочном периоде.
Решение. Равновесие конкурентной фирмы в долгосрочном периоде достигается при равенстве AC=MC=P.
Средние издержки каждой фирмы равны AC = TC/ q → AC = q2 – 6q + 18.
Предельные издержки для каждой фирмы – это производная от общих издержек, то есть MC = ∆TC/ ∆q = TC΄ → MC = 3q2 – 12q + 18.
Приравняем функции AC и MC и определим равновесный объем производства для фирмы:
AC=MC → q2 – 6q + 18 = 3q2 – 12q + 18 → 2q2– 6q = 0.
Отсюда q = 3.
Цена равновесия P = MC. Подставим в функцию MC значение равновесного количества q = 3 → MC = 3q2 – 12q + 18 = 3*32 – 12*3 + 18 = 9.
Каждая фирма продает по цене, сложившейся в отрасли, поэтому отраслевая цена равна:
P = MC = 9.
Общий равновесный объем спроса в отрасли определим в соответствии с функцией спроса Qd = 180-3P = 180 – 3*9 = 153.
Отраслевое предложение в долгосрочном периоде равно Qd = Qs = 153.
Число фирм в долгосрочном периоде: N = Qs/ qs = 153/ 3 = 51.
По условию задачи 30 фирм, следовательно, еще 21 фирма войдет в отрасль.
Задача 4. Общие краткосрочные издержки совершенно конкурентной фирмы описываются уравнением TC = Q3 – 8Q2 + 20Q + 50. Определите минимальную цену, при которой фирма сохранит производство в краткосрочном периоде. Какой объем будет производить фирма? Чему равны предельные издержки при данном объеме производства? Является ли этот объем производства оптимальным?
Решение. Минимальная цена, при которой фирма сохранит производство в краткосрочном периоде – это цена, равная минимальным средним переменным издержкам P=min AVC. При этой цене для фирмы безразлично, сохранить производство или закрыться. Ее выручка полностью возместит только переменные издержки, а убытки будут равны величине постоянных издержек FC=50, также как при нулевом производстве. При более низкой цене фирма прекратит производство, так как цена не позволит полностью возместить переменные издержки, и ее убытки будут больше, чем при закрытии.
1. Для определения цены необходимо определить минимальное значение средних переменных издержек.
Средние переменные издержки определяются по формуле:
, где TVC - общие переменные издержки, Q – объем производства.
Общие переменные издержки TVC можно вычислить исходя из функции общих издержек TC= Q3 – 8Q2 + 20Q + 50, где параметр 50 – это величина постоянных издержек FC (которые не изменяются при изменении объемов производства) как разницу:
TVC = TC–FC = (Q3 – 8Q2 + 20Q + 50) – 50 = → TVC = Q3 – 8Q2 + 20Q.
Отсюда функция средних переменных издержек имеет вид:
AVC = TVC: Q → AVC = (Q3 – 8Q2 + 20Q): Q → AVC = Q2 – 8Q + 20.
2. В точке минимума средних переменных издержек производная от функции равна нулю. Найдем производную от функции AVC:
AVC΄ = (Q2 – 8Q + 20)΄ = 2Q – 8.
Приравняем производную AVC΄ к нулю и определим объем производства Q при минимальном значении AVC:
2Q – 8 = 0, отсюда Q = 4.
Подставим Q = 4 в функцию средних переменных издержек и найдем значение минимальных средних переменных издержек min AVC:
AVC = Q2 – 8Q + 20 → min AVC = 42 – 8*4 + 20 = 16-32+20 = 4.
3. Минимальная цена, при которой фирма сохранит производство в краткосрочном периоде P=min AVC = 4.
4. На основе функции общих издержек или функции переменных издержек можно вычислить величину убытков фирмы.
TC (4) = Q3 – 8Q2 + 20Q + 50 = 43 – 8*42 + 20*4 + 50 = 66ден.ед.
TR = P * Q = 4*4 = 16ден.ед.
Убытки (4) = TR - TC (4) = 66 - 16 =- 50 = FC.
Или → TVC (4) = Q3 – 8Q2 + 20Q = 43 – 8*42 + 20*4 = 16ден.ед.
TR = 16ден. ед., то есть выручка возмещает только переменные издержки TR = TVC4. Следовательно, Убытки(4) равны постоянным издержкам FC(4) = - 50.
При нулевом производстве, если фирма закроет предприятие, не имея выручки от продажи, она будет также получать убытки, равные величине постоянных издержек FC(0) = - 50.
5. Оптимальный объем производства соответствует правилу MR(=P)=MC. Предельные издержки MC равны минимальному значению средних переменных издержек MC = min AVC = 4.
6. Цена также равна минимальному значению AVC и равна 4. То есть при min AVC и при объеме Q = 4ед. достигается равенство предельного дохода и предельных издержек MR(=P) = MC. Это значит, что если фирма сохраняет производство, то объем продукции Q = 4 единицы является оптимальным, наилучшим. Уменьшение или увеличение производства хотя бы на одну единицу приведет к увеличению убытков:
Если Q=5ед. → TC(5) = 75; TR = 4*5ед.=20; Убытки =TR(5)-TC(5)=75-20= -55.
Если Q=3ед. → TC(3) = 65; TR = 4*3ед.=12; Убытки =TR(3)-TC(3)= 6 5-12= -53.
