| Количество блага А | Видеоигры (А) | Количество блага В | Компакт-диски (В) | ||||
| TU | MU | MU/Р=2 | TU | MU | MU/Р=1 | ||
| -3 | -3 |
Легко проверить, что, согласно правилу Дж. Хикса, всякое отклонение от равновесия в рамках существующего дохода приведет к уменьшению общей полезности набора, так как потери полезности от уменьшения одного блага будут больше, чем прирост полезности от увеличения другого блага. По таблице видно, что потери полезности при уменьшении тов. А на одну единицу составят – MU3A = -6, а прирост полезности при увеличении тов. В на две единицы (с учетом цен на товары А и В) составит + MU5B + MU6B = +0 + (-3) = -3 (предельная полезность в данном примере уже стала отрицательной величиной в соответствии с законом убывания предельной полезности). В результате общая полезность уменьшится на -6 и увеличится на -3, то есть в целом уменьшится на -9 и составит 18(TU2A) + 26(TU6B) = 44, что меньше, чем в условиях равновесия (53).
Задача 2. Функция полезности потребителя описывается формулой U = XY/2, где X – объем потребления бананов, Y – объем потребления пепси-колы. Цена 1кг бананов 3дол., 1л пепси-колы – 2дол. летом потребитель тратил на эти товары 20дол в неделю. Зимой цена бананов поднялась до 5дол за килограмм, цена пепси-колы не изменилась. Определите:
1) Объем оптимального потребления бананов и пепси-колы летом.
2) Величину расходов, необходимую зимой для достижения того же уровня полезности, что и летом.
3) Количественное значение эффекта дохода и эффекта замены.
Решение. Бюджетные возможности можно представить в виде равенства: M = PX X + PY Y, где:
X и Y – количество товаров, приобретаемых потребителем;
PX и PY – цена товаров X и Y;
M – доход потребителя.
Бюджетные возможности потребителя при покупке бананов (тов. X) и пепси-колы (тов. Y) летом можно выразить формулой 3X + 2Y = 20.
На основе этой формулы надо построить бюджетную линию. Наклон бюджетной линии определяется обратным соотношением цен и характеризует пропорцию замены или соотношение товаров X и Y в наборе:
NЗ =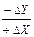 
= 
, или 
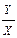= . По условию задачи =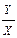 
.
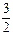Равновесие потребителя достигается в точке касания бюджетной линии с графиком безразличия, где их углы наклона совпадают, а значит, соотношение товаров в наборе на графике безразличия должно соответствовать соотношению товаров на бюджетной линии и определяться соотношением цен. Иными словами для графика безразличия в точке касания MRSxy = ∆Y/ ∆X = Px / Py.
Или, также как для бюджетной линии, соотношение товаров в наборе равно = .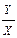
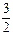Соотношение товаров в наборе определяется соотношением цен, а количество товара X и товара Y зависит от величины дохода.
1. Для определения оптимального набора составим и решим систему уравнений:
1. 3X + 2Y = 20
2. 
= 
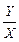Отсюда Y = 3/2 * X → 3X + 2( 3/2*X) = 20 →
3X + 3X = 20, отсюда X = 3,3; соответственно Y = 5.
Оптимальное потребление составит 3,3 кг бананов и 5 л пепси-колы.
Определим величину общей полезности данного набора:
U = XY/2 = (3,3 *5)/2 → U = 8,25.
Эта полезность соответствует всем наборам, находящимся на графике безразличия, который можно вывести из формулы полезности U = XY/2 и выразить функцией Y = 2U/X → Y = 16,5/X
2. Определим набор, соответствующий такому же уровню полезности, но при более высокой цене тов. X.
Соотношение товаров в наборе изменится в связи с увеличением цены бананов (тов. X): =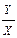 
.
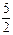Количество товара X и товара Y должно быть таким, чтобы при изменившемся соотношении общая полезность набора не изменилась, то есть новый набор должен находится на существующем графике безразличия. Составим и решим новую систему уравнений с учетом функции полезности:
1. 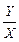= 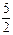→ Y = 5X/2
2. Y = 16,5/X → 16,5 = Y X
16,5 = (5X/2) * X
16,5 = 5X2/2 → 33 = 5X2 → X2 = 6,7 → X = 2,6; Y = X * 5/2 = 6,5.
Набор 2,6 кг бананов и 6,5 л пепси-колы соответствует такому же уровню полезности, что и в первом наборе. Согласно свойствам графика безразличия уменьшение одного блага сопровождалось увеличением другого в такой пропорции, что общая полезность оставалось постоянной величиной.
Определим бюджет потребителя, соответствующий новому равновесному набору, исходя из формулы бюджетных возможностей:
M = PX X + PY Y
M = 5*2,6 + 2*6,5 = 26дол., то есть доход потребителя должен возрасти.
3. Эффект замещения составит (3,3кг – 2,6кг) = - 0,7кг бананов и (6,5кг – 5кг) = + 1,5 пепси-колы.
Эффект дохода. Если бы покупатель тратил зимой на покупки 20дол, то его оптимальный набор при новом соотношении цен составил бы 2кг бананов и 5л пепси-колы. Это можно определить, составив систему уравнений (см. п. 1).
1. 5X + 2Y = 20
2. = 
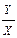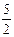
Отсюда Y = 5/2 * X → 5X + 2( 5/2*X) = 20 →
5X + 5X = 20, отсюда X = 2; соответственно Y = 5.
Следовательно, эффект дохода составляет 0,6кг бананов (2,6кг – 2кг) 1,5л пепси-колы (6,5л – 5л).
