1.
| ||||
|
2.
|
| |||||
|
|
3.
|
| ||||
|
|
4.
|
| |||||
|
|
5.
|
| ||||
|
|
6.
|
| ||||
|
|
7.
|
| ||||
|
|
8.
|
| ||||
|
|
9.
|
| ||||
|
|
10.
|
| ||||
|
|
11.
|
| ||||
|
|
12.
|
| ||||
|
|
13.
|
| ||||
|
|
14.
|
| ||||
|
|
15.
|
| ||||
|
|
16.
|
| ||||
|
|
17.
|
| ||||
|
|
18.
|
| ||||
|
|
19.
|
| |||||
|
|
20.
|
| |||||
|
|
21.
|
| ||||
|
|
22.
|
| ||||
|
|
23.
|
| |||||
|
|
24.
|
| ||||
|
|
25.
|
| ||||
|
|
26.
|
| ||||
|
|
27.
|
| |||||
|
|
28.
|
| ||||
|
|
29.
|
| |||||
|
|
30.
|
| |||||
|
|
31.
|
| ||||
|
|
32.
|
| |||||
|
|
33.
|
| ||||
|
|
34.
|
| |||||
|
|
35.
|
| ||||
|
|
36.
|
| ||||
|
|
37.
|
| ||||
|
|
38.
|
| ||||
|
|
39.
|
| ||||
|
|
40.
|
| ||||
|
|
41.
|
| ||||
|
|
42.
|
| ||||
|
|
43.
|
| ||||
|
|
44.
|
| ||||
|
|
45.
|
| |||||
|
|
46.
|
| |||||
|
|
47.
|
| ||||
|
|
48.
|
| ||||
|
|
49.
|
| |||||
|
|
50.
|
| ||||
|
|
Вопросы к экзамену.
1. Дайте определение комплексного числа.
2. Формы записи комплексного числа.
3. Запишите правила сложения, умножения, вычитания и деления комплексных чисел, записанных в алгебраической форме
4. Запишите правила действий над комплексными числами, записанными в тригонометрической форме.
5. Дайте определение предела функции.
6. Дайте определение бесконечно малой и бесконечно большой функций.
7. Сформулируйте теоремы о пределах.
8. Дайте определение производной функции.
9. В чем состоит геометрический смысл производной?
10. В чем состоит физический смысл производной?
11. Дайте определение второй производной функции.
12. В чем состоит физический смыл второй производной?
13. Напишите все формулы дифференцирования.
14. Сформулируйте условие постоянства функции.
15. Сформулируйте условия возрастания и убывания функции.
16. Сформулируйте необходимое условие существования экстремума функции.
17. Сформулируйте достаточное условие существования экстремума функции.
18. Как найти точки экстремума и экстремумы функции?
19. Как найти наименьшее и наибольшее значения функции на отрезке?
20. Сформулируйте условия выпуклости и вогнутости кривой.
21. Как найти направление вогнутости и точки перегиба кривой?
22. Какое действие называется интегрированием?
23. Какая функция называется первообразной для функции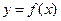 
?
24. Дайте определение неопределенного интеграла.
25. Перечислите основные свойства неопределенного интеграла.
26. Каким действием можно проверить интегрирование?
27. Напишите основные формулы интегрирования (табличные интегралы).
28. Дайте определение определенного интеграла.
29. Перечислите основные свойства определенного интеграла.
30. В чем заключается геометрический смысл определенного интеграла?
31. Напишите формулы для определенного интеграла.
32. Какое уравнение называется дифференциальным?
33. Дайте определение дифференциального уравнения первого порядка.
34. Дайте определение общего решения и общего интеграла дифференциального уравнения первого порядка.
35. Дайте определение частного решения и частного интеграла дифференциального уравнения первого порядка.
36. Какое событие называется невозможным; достоверным?
37. Какие события называются несовместными; равновозможными?
38. Какие события образуют полную систему событий?
39. Что понимается под вероятностью события?
40. Дайте классическое определение вероятности события.
41. Какие задачи решает математическая статистика?
42. Что называется полигоном частот?
43. Дайте определение генеральной, выборочной совокупности?
СОДЕРЖАНИЕ.
пояснительная записка.. 3
ЛИТЕРАТУРА.. 3
Общие методические указания.. 4
СОДЕРЖАНИЕ УЧЕБНОЙ ДИСЦИПЛИНЫ………………………………………………………….5
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ № 1 …………….8
Комплексные числа……………………………………………………………………………………….8
Предел функции………………………………………………………………………………………….12
Дифференциальное исчисление ………………………………………………………………………..15
Интегральное исчисление……………………………………………………………………………….27
Дифференциальные уравнения…………………………………………………………………………38
Теория вероятностей и математическая статистика…………………………………………………...43
ЗАДАНИЯ НА КОНТРОЛЬНУЮРАБОТУ……………………………………………………………51
Задачи № 1 - 50. Комплексные числа…………………………………………………………………...52
Задачи № 1 - 50. Вычислите предел функции………………………………………………………….53
Задачи № 1 - 50. Исследовать функцию и построить график…………………………………………54
Задачи № 1 - 50. Вычислить площадь фигуры, ограниченной линиями……………………………..56
Задачи № 1-50. Решите дифференциальные уравнения и найдите частные решения, удовлетворяющие данным условиям. 57
Задачи № 1-50. Решить дифференциальное уравнение II порядка. 58
Задачи № 1-50. Решить задачи. 60
Задачи № 1-50 Задано распределение частот выборочной совокупности объема 
. Написать распределение относительных частот; построить полигон относительных частот. 62
Вопросы к экзамену.. 65
