Тема 2: Элементы теории множеств
Основной уровень
Задание 1. Принадлежат ли данному множеству объекты?
1.1 F – множество фруктов. Принадлежит ли этому множеству: а) яблоко; б) арбуз; в) груша; г) апельсин; д) морковь; е) кокос.
1.2 S – множество спортивных игр. Принадлежит ли этому множеству: а) футбол; б) волейбол; в) регби; г) самбо; д) спортлото; е) бобслей.
1.3 С – множество видов борьбы. Принадлежит ли этому множеству: а) дзюдо; б) самбо; в) каратэ; г) рестлинг; д) сумо; е) у-шу.
1.4 D – множество деревьев. Принадлежит ли этому множеству: а) яблоня; б) лиственница; в) боярышник; г) апельсин; д) пихта; е) ромашка.
1.5 L – множество школьных предметов (дисциплин). Принадлежит ли этому множеству: а) химия; б) черчение; в) фехтование; г) биология; д) история; е) этикет.
1.6 В – множество букв русского алфавита. Принадлежит ли этому множеству: а) Ы; б) α; в) Щ; г) $; д) Б; е) Ф.
1.7 К – множество экстремальных видов спорта. Принадлежит ли этому множеству: а) ВМХ-байк; б) альпинизм; в) танка; г) паркур; д) коррида; е) дайвинг.
1.8 V – множество глаголов. Принадлежит ли этому множеству: а) поющий; б) шагать; в) просить; г) запрещать; д) спать; е) созерцать.
1.9 А – множество олимпийских видов спорта. Принадлежит ли этому множеству: а) хоккей с шайбой; б) спортивная гимнастика; в) пауэрлифтинг; г) легкая атлетика; д) спортивная акробатика; е) фигурное катание.
1.10 Е – множество стран Европы. Принадлежит ли этому множеству: а) Англия; б) Монголия; в) Испания; г) Польша; д) Греция; е) Бразилия.
Задание 2. Запишите с помощью символа принадлежности:
2.1 Принадлежит ли число: 1) 2 множеству (2; 10); 2) –0,25 множеству [-0,5; 0]; 3) 72 множеству Q; 4) 5,3 множеству Z?
2.2 Принадлежит ли число: 1) 3 множеству (2; 10); 2) –0,5 множеству [-0,5; 0]; 3) 7,2 множеству Q; 4) -5,3 множеству Z?
2.3 Принадлежит ли число: 1) -2 множеству (2; 10); 2) 0,25 множеству [-0,5; 0]; 3) -72 множеству Q; 4) 53 множеству Z?
2.4 Принадлежит ли число: 1) 7 множеству (2; 10); 2) –0,5 множеству [-0,5; 0,5]; 3) 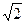 множеству Q; 4) 53 множеству Z?
множеству Q; 4) 53 множеству Z?
2.5 Принадлежит ли число: 1) 0,2 множеству (-2; 0); 2) 0,125 множеству [-0,5; 0,5]; 3) 72 множеству R; 4) -5 множеству Z?
2.6 Принадлежит ли число: 1) 0,3 множеству (0,2; 1); 2) –0,75 множеству [-0,5; 0]; 3)  множеству Q; 4) 3 множеству Z?
множеству Q; 4) 3 множеству Z?
2.7 Принадлежит ли число: 1) 8 множеству (2; 10); 2) 0,175 множеству [-0,5; 0,5]; 3)  множеству R; 4) -1 множеству Z?
множеству R; 4) -1 множеству Z?
2.8 Принадлежит ли число: 1) 22 множеству (22; 30); 2) –0,135 множеству [-0,5; 0]; 3) -7,5 множеству Q; 4) 0,3 множеству Z?
2.9 Принадлежит ли число: 1) -0,5 множеству (-2; 0); 2) 2,5 множеству [-0,5; 2]; 3)  множеству Q; 4) 53 множеству Z?
множеству Q; 4) 53 множеству Z?
2.10 ринадлежит ли число: 1) 7 множеству (2; 10); 2) 2,5 множеству [5; 7]; 3) 386,45 множеству Q; 4) -5,7 множеству Z?
Задание 3. Множества заданы характеристическими свойствами. Задайте их перечислением:
3.1 Запишите множество: а) букв в слове «критик»; б) цифр в записи числа 5125353; в) { x | x Î N, 2<x<8 }.
3.2 Запишите множество: а) букв в слове «сосна»; б) цифр в записи числа 5315253; в) { x | x Î N, 3≤x<9 }.
3.3 Запишите множество: а) букв в слове «осколок»; б) цифр в записи числа 3525315; в) { x | x Î N, 1<x<7 }.
3.4 Запишите множество: а) букв в слове «дидактика»; б) цифр в записи числа 5125253; в) { x | x Î N, 21<x<36 }.
3.5 Запишите множество: а) букв в слове «кокос»; б) цифр в записи числа 3535215; в) { x | x Î N, 12<x<18 }.
3.6 Запишите множество: а) букв в слове «баобаб»; б) цифр в записи числа 1255353; в) { x | x Î N, 34<x<48 }.
3.7 Запишите множество: а) букв в слове «шалаш»; б) цифр в записи числа 1525353; в) { x | x Î N, 3<x≤8 }.
3.8 Запишите множество: а) букв в слове «рококо»; б) цифр в записи числа 1255353; в) { x | x Î N, 2≤x<7 }.
3.9 Запишите множество: а) букв в слове «банан»; б) цифр в записи числа 5531253; в) { x | x Î N, 11<x<21 }.
3.10 Запишите множество: а) букв в слове «цитата»; б) цифр в записи числа 5351253; в) { x | x Î N, 45≤x≤50 }.
Задание 4. Дано множество. Составьте все его подмножества.
4.1 К = {21, 54, 80}.
4.2 К = {21, 80, 153}.
4.3 К = {21, 54, 153}.
4.4 К = {21, 54, 171}.
4.5 К = {21, 153, 171}.
4.6 К = {54, 80,171}.
4.7 К = {80, 171, 234}.
4.8 К = {153, 171, 234}.
4.9 К = {21, 171, 234}.
4.10 К = {21, 43, 71}.
Задание 5. Даны множества А и В. Найдите AUB, А∩В, А\В и В\А. Изобразите графически результат.
5.1 А = {12; 20; 48; 60; 90}, В = {48; 60; 90}.
5.2 А = {1; 2; 4; 6; 9}, В = {4; 8; 9}.
5.3 А = {2; 12; 18; 28; 30}, В = {18; 20; 30}.
5.4 А = {11; 12; 13; 16; 18}, В = {11; 12; 14}.
5.5 А = {-12; -10; -8; 0; 9}, В = {-8; 0; 10}.
5.6 А = {1,2; 2,03; 4,8; 6,01; 9,02}, В = {4,8; 6,01; 9,02}.
5.7 А = {3; 5; 7; 9; 10}, В = {3; 6; 9}.
5.8 А = {12; 20; 48; 60; 90}, В = {48; 60; 90}.
5.9 А = {13; 23; 43; 63; 93}, В = {43; 62; 91}.
5.10 А = {4; 24; 48; 65; 93}, В = {48; 65; 90}.
Задание 6. Укажите, какие из данных множеств являются конечными, бесконечными, пустыми:
6.1 а) М – множество действительных корней квадратного уравнения х2+1=0; б) М – множество всех четных чисел; в) М – множество студентов КГУ; г) М – множество городов России.
6.2 а) М – множество действительных корней квадратного уравнения х2+2х+1=0; б) М – множество всех целых чисел; в) М – множество студентов КГУ; г) М – множество юношей в группе студентов.
6.3 а) М – множество действительных корней квадратного уравнения х2+7=0; б) М – множество всех положительных иррациональных чисел; в) М – множество парт в аудитории; г) М – множество стран Европы.
6.4 а) М – множество действительных корней квадратного уравнения х2+x+1=0; б) М – множество прямоугольных треугольников, у которых квадрат гипотенузы не равен сумме квадратов катетов; в) М – множество океанов; г) М – множество книг в библиотеке.
6.5 а) М – множество действительных корней квадратного уравнения 2 х2 +5х–1=0; б) М – множество всех четных чисел; в) М – множество букв русского алфавита; г) М – множество пальцев на правой руке.
6.6 а) М – множество действительных корней квадратного уравнения х2-9=0; б) М – множество всех нечетных чисел; в) М – множество цифр; г) М – множество деревень России.
6.7 а) М – множество действительных корней квадратного уравнения х2+1-4х=0; б) М – множество всех прямоугольников; в) М – множество преподавателей КГУ; г) М – множество материков планеты Земля.
6.8 а) М – множество действительных корней квадратного уравнения х2-6x+3=0; б) М – множество всех четных чисел; в) М – множество факультетов университета; г) М – множество берез в бору.
6.9 а) М – множество действительных корней квадратного уравнения х2+9=0; б) М – множество натуральных чисел; в) М – множество композиторов XIX в.; г) М – множество жителей Москвы.
6.10 а) М – множество действительных корней квадратного уравнения х2+2х+8=0; б) М – множество спутников Земли; в) М – множество действительных чисел; г) М – множество художников ХХ в.
Повышенный уровень
Задание 1. Определите, принадлежат ли объекты данному множеству:
1.1 М – множество предметов спортивного инвентаря. Принадлежит ли этому множеству: а) ракетка; б) мяч; в) скакалка; г) ведро; д) брусья; е) молоток.
1.2 М – множество настольных игр. Принадлежит ли этому множеству: а) шахматы; б) шашки; в) домино; г) дартс; д) лото; е) буриме.
1.3 М – множество овощей. Принадлежит ли этому множеству: а) томат; б) огурец; в) кабачок; г) арбуз; д) картофель; е) клубника.
1.4 М – множество четырехугольников. Принадлежит ли этому множеству: а) ромб; б) трапеция; в)окружность; г) прямоугольник; д) гипотенуза; е) квадрат.
1.5 М – множество фруктов. Принадлежит ли этому множеству: а) арбуз; б) яблоко; в) тыква; г) груша; д) слива; е) персик.
Задание 2. Множества заданы характеристическими свойствами. Задайте их перечислением:
2.1 Запишите множество: а) букв в слове «постоянство»; б) цифр в записи числа 4648241; в) { x | x Î Z, x Î [-3; 2]}.
2.2 Запишите множество: а) букв в слове «абракадабра»; б) цифр в записи числа 8642144; в) { x | x Î Z, x Î [-10; 0]}.
2.3 Запишите множество: а) букв в слове «милитаризм»; б) цифр в записи числа 8464241; в) { x | x Î Z, x Î [-3; 1]}.
2.4 Запишите множество: а) букв в слове «картография»; б) цифр в записи числа 1464824; в) { x | x Î Z, x Î [-4; 6]}.
2.5 Запишите множество: а) букв в слове «математика»; б) цифр в записи числа 4641824; в) { x | x Î Z, x Î [-13; -2]}.
Задание 3. Дано множество К = {21, 54, 80, 153, 171, 234}. Составьте подмножество множества К с заданным свойством.
3.1 Составьте подмножество К из чисел, которые делятся на 3.
3.2 Составьте подмножество К из чисел, которые не делятся на 3.
3.3 Составьте подмножество К из чисел, которые делятся на 4.
3.4 Составьте подмножество К из чисел, которые не делятся на 2.
3.5 Составьте подмножество К из чисел, которые делятся на 9.
Задание 4. Даны множества: A, B, C и D. Найдите: 1) A\(BUD); 2) C∩DU(A\B); 3) (CUA)∩(B\D).
4.1 A = {21; 12; 11; 22}, B = {11; 12; 13; 14; 15}, C = {51; 15; 31}, D = {11; 13; 14; 15}.
4.2 A = {1; 2; 10; 12}, B = {1; 2; 3; 4; 5}, C = {5; 10; 11}, D = {1; 3; 4; 5}.
4.3 A = {25; 13; 11; 22}, B = {11; 12; 13; 14; 15}, C = {53; 35; 13}, D = {11; 13; 16; 118}.
4.4 A = {10; 12; 13; 22}, B = {11; 12; 15; 16; 17}, C = {51; 15; 31}, D = {10; 13; 14; 15}.
4.5 A = {2; 12; 13; 22}, B = {11; 12; 13; 14; 15}, C = {11; 15; 31}, D = {2; 13; 14; 31}.
Задание 5. Укажите, какие из данных множеств являются конечными, бесконечными, пустыми:
5.1 а) М – множество действительных корней квадратного уравнения 3х2+5х+6=0; б) М – множество иррациональных чисел; в) М – множество действительных чисел, квадрат которых равен 2; г) М – множество городов «Золотого кольца» России.
5.2 а) М – множество действительных корней квадратного уравнения 2х2+3х+4=0; б) М – множество целых чисел; в) М – множество картин «Эрмитажа»; г) М – множество цветов радуги.
5.3 а) М – множество действительных корней квадратного уравнения 2х2+3х+8=0; б) М – множество поэтов ХХ в.; в) М – множество страниц в книге; г) М – множество положительных целых чисел.
5.4 а) М – множество действительных корней квадратного уравнения 3х2+2х+7=0; б) М – множество минут в сутках; в) М – множество кнопок сотового телефона; г) М – множество окружностей с целочисленным радиусом.
5.5 а) М – множество действительных корней квадратного уравнения 3х2+4х+5=0; б) М – множество зубов у амебы; в) М – множество первокурсников университета; г) М – множество прямых, параллельных данной прямой m.
Задание 6. Решите задачу, используя формулу Грассмана:
6.1 Каждый ученик в классе изучает английский или французский язык. Английский язык изучают 25 человек, французский – 27 человек, а тот и другой – 18 человек. Сколько учеников в классе?
6.2 Каждый из членов команды играет либо в футбол, либо в теннис, либо в футбол и в теннис. Сколько человек в команде, если известно, что 18 человек играют в обе игры, 23 человека играют в футбол, 21 – в теннис?
6.3 В старшей группе детского сада 28 детей. Из них 17 детей умеют считать, а 9 – читать и считать. Сколько детей умеют читать?
6.4 Определить число студентов в группе, если 15 из них изучают английский язык, 12 – немецкий, 3 – оба языка, 1 – ни одного.
6.5 На листе бумаги начертили круг площадью 78 см2 и квадрат площадью 55 см2. Площадь пересечения круга и квадрата равна 30 см2. Не занятая кругом и квадратом часть листа имеет площадь 150 см2. Найдите площадь листа.
Тема 3: Элементы математической логики
Основной уровень
Задание 1. Укажите, какие из данных предложений являются высказываниями или высказывательными формами, не являются высказываниями или высказывательными формами:
1.1 а) Курган – столица России; б) Студент университета; в) Треугольник АВС подобен треугольнику А1В1С1; г) Луна – спутник Марса.
1.2 а) Кислород – газ; б) Каша – вкусное блюдо; в) Математика – интересный предмет; г) Картины Пикассо слишком абстрактны.
1.3 а) Железо тяжелее свинца; б) Да здравствуют музы!; в) Треугольник называется равносторонним, если все его стороны равны; г) Если в треугольнике все углы равны, то он равносторонний.
1.4 а) Сегодня плохая погода; б) В романе А.С. Пушкина «Евгений Онегин» 136 245 букв; в) Река Ангара впадает в озеро Байкал; г) Число 12345 кратно 3.
1.5 а) Чтобы подключиться к Интернету с домашнего компьютера, необходим модем и соответствующее программное обеспечение; б) Солнце светит для всех; в) Все ученики любят информатику; г) Некоторые из учеников любят информатику.
1.6 а) А ты любишь информатику?; б) Посмотри в окно; в) Крокодилы летают очень низко; г) Число 8456 является совершенным.
1.7 а) Без труда не выловишь и рыбку из пруда; б) Как хорошо быть генералом!; в) Революция может быть мирной и немирной; г) Зрение бывает нормальное, или у человека имеется дальнозоркость или близорукость.
1.8 а) Познай самого себя; б) Не может быть, что ни один человек не дышит жабрами; в) Талант всегда пробьет себе дорогу; г) Некоторые животные мыслят.
1.9 а) Информатика, в частности, изучает алгоритмы; б) Всякая истина является конкретной; в) Это утверждение ложно; г) Человек – брюнет.
1.10 а) Существует жизнь после смерти; б) Шел дождь; в) Число у делится на 7; г) 3 + 2 = 5.
Задание 2. Формализуйте данные сложные высказывания:
2.1 а) «Луна - планета и 2 + 3 = 5»; б) «Если 17 делится на 4, то оно делится на 2»; в) «12 делится на 6 тогда и только тогда, когда оно делится на 3»; г) «Если на улице холодно и сыро, мы не пойдем в лес».
2.2 а) «Луна – планета или 2 + 3 = 5»; б) «Если 20 делится на 4, оно делится на 2»; в) «11 делится на 6 тогда и только тогда, когда оно делится на 3»; г) «На улице не холодно или на улице не сыро».
2.3 а) «1 – простое число и 2 – простое число»; б) «Если Солнце всходит на востоке, то оно заходит на западе»; в) «15 делится на 6 тогда и только тогда, когда оно делится на 3»; г) «Здесь холодно, и было бы хорошо, если бы ты закрыл окно».
2.4 а) «1 – простое число или 2 – простое число»; б) «Если Солнце всходит на юге, то оно заходит на западе»; в) «15 делится на 3 тогда и только тогда, когда оно делится на 6»; г) «Если какое-то вещество нагревать, оно расплавится или испарится, но оно может также и взорваться».
2.5 а) «Кислород – металл и 2 ´ 2 = 5»; б) «Если Солнце всходит на востоке, то оно заходит на севере»; в) «12 делится на 6 тогда и только тогда, когда 12 делится на 3»; г) «Если завтра выпадет снег, мы пойдем в лес на лыжах и возьмем с собой собаку».
2.6 а) «Кислород – металл или 2 ´ 2 = 5»; б) «Если Солнце всходит на севере, то оно заходит на западе»; в) «11 делится на 6 тогда и только тогда, когда 11 делится на 3»; г) «Если свет имеет волновую природу, то когда он представляется в виде потока частиц (корпускул), допускается ошибка».
2.7 а) «Цинк – металл и цезий – металл»; б) «Если Москва – большой город, то Солнце заходит на западе»; в) «15 делится на 6 тогда и только тогда, когда 15 делится на 3»; г) «Если данное число делится на 6, то оно делится на 2 и делится на 3».
2.8 а) «Цинк – металл или цезий – металл»; б) «Если Москва – большой город, то Солнце заходит на юге»; в) «15 делится на 5 тогда и только тогда, когда 15 делится на 4»; г) «Если данное число делится на 8, то оно является четным или делится на 16».
2.9 а) «Каждое число делится на 2 или делится на 3»; б) «Если 2 ´ 2 = 5, то Нью-Йорк – маленький город»; в) «15 делится на 5 тогда и только тогда, когда 15 делится на 4»; г) «Если вы были в Париже, то вы видели Лувр или видели Эйфелеву башню».
2.10 а) «Эйфелева башня находится в Париже или она находится в Нью-Йорке»; б) «Если 2 ´ 2 = 5, то Нью-Йорк – большой город»; в) «Солнце восходит на востоке тогда и только тогда, когда оно заходит на западе»; г) «Если мистер Джонс счастлив, то миссис Джонс несчастлива и если мистер Джонс несчастлив, то миссис Джонс счастлива».
Задание 3. По форме высказываний и выраженным на естественном языке составляющим его простым высказываниям получите фразу на естественном языке. 1)  ; 2)
; 2) 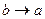 ; 3)
; 3) 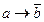 ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  ; 10)
; 10)  ; 11)
; 11)  ; 12)
; 12)  ; 13)
; 13)  ; 14)
; 14)  ; 15)
; 15)  ; 16)
; 16)  .
.
3.1 а = «8 – четное число»; b = «8 делится на 4»
3.2 а = «Все дети любят манную кашу»; b = «Все дети хорошо растут»
3.3 а = «Самолеты летают высоко»; b = «Самолеты падают очень редко»
3.4 а = «Собака бывает кусачей»; b = «Собака живет в будке»
3.5 а = «9 – нечетное число»; b = «9 делится на 3»
3.6 а = «Лошади умеют летать»; b = «Лошади высоко прыгают»
3.7 а = «Ночью все кошки серы»; b = «Найти черную кошку в черной комнате очень легко»
3.8 а = «Историк Гуськов увлекается математикой»; b = «Математика помогает изучать историю»
3.9 а = «6 – четное число»; b = «6 делится на 4»
3.10 а = «Все спортсмены – здоровые люди»; b = «Спорт помогает вести здоровый образ жизни»
Задание 4. Составьте таблицы истинности для формул:
4.1 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
4.2 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
4.3 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
4.4 1)  ; 2)
; 2)  ; 3)
; 3) 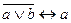 .
.
4.5 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
4.6 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
4.7 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
4.8 1) 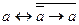 ; 2)
; 2)  ; 3)
; 3)  .
.
4.9 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
4.10 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Задание 5. Укажите, какие из формул в предыдущей задаче являются тавтологиями, противоречиями, выполнимыми (опровержимыми).
Задание 6. С помощью таблиц истинности проверьте, какие из данных формул являются равносильными:
6.1 F =  ; G =
; G =  ; H =
; H =  .
.
6.2 F =  ; G =
; G =  ; H =
; H =  .
.
6.3 F =  ; G =
; G =  ; H =
; H =  .
.
6.4 F =  ; G =
; G =  ; H =
; H =  .
.
6.5 F =  ; G =
; G =  ; H =
; H =  .
.
6.6 F =  ; G =
; G =  ; H =
; H =  .
.
6.7 F = 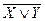 ; G =
; G =  ; H =
; H =  .
.
6.8 F =  ; G =
; G =  ; H =
; H =  .
.
6.9 F =  ; G =
; G =  ; H =
; H =  .
.
6.10 F =  ; G =
; G = 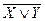 ; H =
; H =  .
.
Повышенный уровень
Задание 1. Укажите, какие из данных предложений являются высказываниями или высказывательными формами, не являются высказываниями или высказывательными формами:
1.1 а) Число слов в этом предложении равно семи; б) В четырехугольнике противоположные стороны равны; в) Во всяком четырехугольнике противоположные стороны равны; г) Существует наибольшее натуральное число.
1.2 а) Осень – лучшая пора года; б) Небо над Сицилией всегда голубое; в) Сожалею, но вы мне не нравитесь; г) Ни одно простое число не является четным.
1.3 а) Глина – это жидкость или газ; б) Из елки можно сделать палку, но из палки не сделаешь елку; в) Фенхель лучше всего растет на участках со сравнительно влажной, слегка кислой почвой; г) Некоторые птицы не летают.
1.4 а) Если воробей – птица, он летает; б) Каждый квадрат является ромбом; в) У ромба диагонали взаимно перпендикулярны; г) Когда идет дождь, все небо покрыто тучами.
1.5 а) Число является простым, если и только если оно делится только на единицу и на само себя; б) Холодный и пустынный дом; в) Если металл нагревается, он плавится; г) Неправда, что философские споры неразрешимы.
Задание 2. Формализуйте данные сложные высказывания:
2.1 а) «Лев Толстой написал роман «Воскресение» или он написал роман «Анна Каренина»»; б) «Тот, кто изучал геометрию, знает теорему Пифагора или, во всяком случае, слышал о ней, а если эта теорема ему неизвестна, ему нетрудно будет понять ее».
2.2 а) «Число 2 четное или оно простое»; б) «Если у меня будет свободное время и не будет дождя, то я не буду писать сочинение, а пойду на дискотеку».
2.3 а) «2 ´ 2 = 4 или белые медведи живут в Африке»; б) «Лошадь погибает от одного грамма никотина, но я не лошадь, следовательно, курить вредно».
2.4 а) «Если Париж расположен на Темзе, то белые медведи обитают в Африке»; б) «Без Вас хочу сказать Вам много,/ При Вас я слушать Вас хочу».
2.5 а) «Если я – Наполеон, то у кошки четыре ноги»; б) «Люди получают высшее образование тогда, когда они заканчивают институт, университет или академию».
Задание 3. По форме высказываний и выраженным на естественном языке составляющим его простым высказываниям получите фразу на естественном языке. 1)  ; 2)
; 2)  ; 3)
; 3) 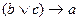 ; 4)
; 4)  ; 5)
; 5)  ; 6)
; 6)  ; 7)
; 7)  ; 8)
; 8)  .
.
3.1 а = «Теория Дарвина является научной»; b = «Теория Дарвина может быть подтверждена опытными данными»; с = «Теория Дарвина может быть опровергнута опытными данными».
3.2 а = «Свидетель был запуган»; b = «Свидетель видел преступника»; с = «Свидетель запомнил номера скрывшейся машины».
3.3 а = «Обезьяну можно научить играть на скрипке»; b = «Обезьяна очень умна»; с = «Обезьяна может запоминать порядок выполнения операций».
3.4 а = «Ребенок требует к себе повышенного внимания»; b = «Ребенок очень устал»; с = «Ребенок хочет есть».
3.5 а = «Работать на компьютере интересно»; b = «Работать на компьютере полезно»; с = «Работать на компьютере вредно для здоровья».
Задание 4. Составьте таблицы истинности для формул:
4.1 1)  ; 2)
; 2)  ; 3)
; 3) 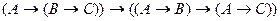 .
.
4.2 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
4.3 1)  ; 2)
; 2)  ; 3)
; 3) 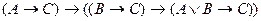 .
.
4.4 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
4.5 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Задание 5. Укажите, какие из формул в предыдущей задаче являются тавтологиями, противоречиями, выполнимыми (опровержимыми).
Задание 6. С помощью таблиц истинности проверьте, какие из данных формул являются равносильными:
6.1 F = 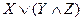 ; G =
; G =  ; H =
; H =  .
.
6.2 F=  ; G =
; G = 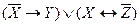 ; H =
; H =  .
.
6.3 F =  ; G =
; G =  ; H =
; H =  .
.
6.4 F =  ; G =
; G = 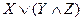 ; H =
; H =  .
.
6.5 F =  ; G =
; G =  ; H =
; H =  .
.
Тема 4: Элементы комбинаторики
Основной уровень
Задание 1. Вычислите: а)  , б)
, б)  . (п – номер варианта)
. (п – номер варианта)
Задание 2. Вычислите а)  , б)
, б)  , в)
, в) 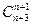 . (п – номер варианта)
. (п – номер варианта)
Задание 3. Решите задачу:
3.1 Сколько двузначных чисел можно составить из цифр 1, 3, 5, 7, 9? Сколько среди них чисел, кратных 5?
3.2 Сколько двузначных чисел можно составить из цифр 1, 3, 5, 7, 9? Сколько среди них чисел, кратных 11?
3.3 Сколько двузначных чисел можно составить из цифр 1, 3, 5, 7, 9? Сколько среди них чисел, кратных 3?
3.4 Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех вертикальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг. Сколько всего стран могут использовать такую символику? Сколько всего стран могут использовать такую символику с верхней белой полосой?
3.5 Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех вертикальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг. Сколько всего стран могут использовать такую символику? Сколько всего стран могут использовать такую символику с нижней зеленой полосой?
3.6 Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех вертикальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг. Сколько всего стран могут использовать такую символику? Сколько всего стран могут использовать такую символику с синей и красной полосами, расположенными рядом?
3.7 В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий, зеленый или желтый цвета, причем были представлены все возможные варианты. Сколько команд участвовали в турнире? Сколько команд играли в зеленых футболках?
3.8 В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий, зеленый или желтый цвета, причем были представлены все возможные варианты. Сколько команд участвовали в турнире? У скольких команд футболки и трусы были разного цвета?
3.9 В футбольном турнире участвуют несколько команд. Оказалось, что все они для трусов и футболок использовали белый, красный, синий, зеленый или желтый цвета, причем были представлены все возможные варианты. Сколько команд участвовали в турнире? У скольких команд футболки и трусы были разного цвета, причем трусы были не красные?
3.10 В клетки квадратной таблицы 2x2 произвольно ставят крестики и нолики. Сколькими способами можно заполнить эту таблицу? В скольких случаях в левой нижней клетке будет стоять крестик?
Задание 4. Решите задачу:
4.1 Вова точно помнит, что в формуле оксида азота подряд идут буквы Н и О и что есть один нижний индекс – то ли двойка, то ли тройка. Нарисуйте дерево возможных вариантов, из которых Вове придется выбирать ответ. Сколько имеется вариантов, в которых индекс равен двойке?
4.2 Вова точно помнит, что в формуле оксида азота подряд идут буквы Н и О и что есть один нижний индекс – то ли двойка, то ли тройка. Нарисуйте дерево возможных вариантов, из которых Вове придется выбирать ответ. Сколько имеется вариантов, в которых индекс стоит на первом месте?
4.3 Вова точно помнит, что в формуле оксида азота подряд идут буквы Н и О и что есть один нижний индекс – то ли двойка, то ли тройка. Нарисуйте дерево возможных вариантов, из которых Вове придется выбирать ответ. Сколько имеется вариантов, в которых индекс стоит на втором месте?
4.4 Одновременно происходят выборы мэра города и префекта округа. На должность мэра выставили свои кандидатуры Алкин, Балкин, Валкин, а на должность префекта – Эшкин, Юшкин, Яшкин. Нарисуйте дерево возможных вариантов голосования и определите с его помощью число различных исходов. В скольких вариантах будет кандидатура Эшкина?
4.5 Одновременно происходят выборы мэра города и префекта округа. На должность мэра выставили свои кандидатуры Алкин, Балкин, Валкин, а на должность префекта – Эшкин, Юшкин, Яшкин. Нарисуйте дерево возможных вариантов голосования и определите с его помощью число различных исходов. В скольких вариантах фамилии кандидатов на должность мэра и на должность префекта состоят из разного числа букв?
4.6 Одновременно происходят выборы мэра города и префекта округа. На должность мэра выставили свои кандидатуры Алкин, Балкин, Валкин, а на должность префекта – Эшкин, Юшкин, Яшкин. Нарисуйте дерево возможных вариантов голосования и определите с его помощью число различных исходов. Как изменится ответ, если учесть еще кандидата «против всех»?
4.7 Из четырех тузов поочередно выбирают два. Нарисуйте дерево возможных вариантов. В скольких случаях среди выбранных будет бубновый туз?
4.8 Из четырех тузов поочередно выбирают два. Нарисуйте дерево возможных вариантов. В скольких случаях вторым выбранным будет туз пик?
4.9 Из четырех тузов поочередно выбирают два. Нарисуйте дерево возможных вариантов. В скольких случаях тузы будут разного цвета?
4.10 У Аси есть любимый костюм, в котором она ходит в школу. Она одевает к нему белую, голубую, розовую или красную блузку, а в качестве «сменки» берет босоножки или туфли. Нарисуйте дерево возможных вариантов Асиной одежды. Сколько дней Ася сможет выглядеть по-новому в этом костюме?
Задание 5. Решите задачу, используя правила умножения и сложения и формулы сочетаний, размещений и перестановок.
5.1 «Вороне где-то Бог послал кусочек сыра», брынзы, колбасы, сухарика и шоколада. «На ель Ворона взгромоздясь, позавтракать совсем уж было собралась, да призадумалась»:
а) если есть кусочки по очереди, то из скольких вариантов придется выбирать;
б) сколько получится «бутербродов» из двух кусочков;
в) если съесть сразу три кусочка, а остальные спрятать, то из скольких вариантов придется выбирать;
г) сколько получится вариантов, если какой-то кусочек все-таки бросить Лисе, а потом ответить на вопрос пункта а)?
5.2 «Проказница Мартышка, Осел, Козел и косолапый Мишка затеяли сыграть квартет». Сколькими способами они могут:
а) по одному сесть за выбранные четыре инструмента;
б) выбрать 5 инструментов из 12 данных;
в) по одному сесть за какие-то 4 из выбранных 5 инструментов из 12 данных;
г) выгнать одного, не имеющего слуха, и потом сыграть на каких-то трех из выбранных 5 инструментов из 12 данных?
5.3 Из колоды в 36 карт вынимают 5 карт. Найдите:
а) число всех возможных вариантов выбора;
б) число вариантов, при которых среди полученных карт есть 4 туза;
в) число вариантов, при которых все полученные карты – пики;
г) число вариантов, при которых все полученные карты – одной масти.
5.4 По списку в 9 классе 15 девочек и 13 мальчиков. Нужно выбрать трех дежурных по классу. Сколькими способами это можно сделать:
а) все члены этой группы должны быть девочками;
б) все члены этой группы должны быть мальчиками;
в) в группе должны быть 1 девочка и 2 мальчика;
г) в группе должны быть 2 девочки и 1 мальчик?
5.5 По списку в 9 классе 15 девочек и 13 мальчиков. Нужно выделить группу из трех человек для посещения заболевшего одноклассника. Сколькими способами это можно сделать, если:
а) все члены этой группы должны быть девочками;
б) все члены этой группы должны быть мальчиками;
в) в группе должны быть 1 девочка и 2 мальчика;
г) в группе должны быть 2 девочки и 1 мальчик?
5.6 По списку в 9 классе 15 девочек и 13 мальчиков. Нужно выделить группу из трех человек для посещения заболевшей одноклассницы. Сколькими способами это можно сделать, если:
а) все члены этой группы должны быть девочками;
б) все члены этой группы должны быть мальчиками;
в) в группе должны быть 1 девочка и 2 мальчика;
г) в группе должны быть 2 девочки и 1 мальчик?
5.7 В оперном театре 10 певцов и 8 певиц, а в опере по замыслу композитора 5 мужских и 3 женских партии. Сколько существует различных певческих составов для спектакля, если известно, что:
а) певцы А и Б ни за что не будут петь вместе;
б) певец А будет петь тогда и только тогда, когда будет петь певица В;
в) 6 певцов накануне сорвали голос на футболе, и одной певице придется петь мужскую партию;
г) все певцы и певицы прекрасно ладят между собой?
5.8 а) Составьте таблицу из двух строк, расположив в первой строке числа k от 0 до 5, во второй строке – числа  ; б) При каком значении числа k получится наибольшее значение числа
; б) При каком значении числа k получится наибольшее значение числа  ? в) Найдите сумму чисел во второй строке составленной таблицы; г) Отметьте на координатной плоскости точки (k;
? в) Найдите сумму чисел во второй строке составленной таблицы; г) Отметьте на координатной плоскости точки (k;  ).
).
5.9 а) Составьте таблицу из двух строк, расположив в первой строке числа k от 0 до 5, во второй строке – числа  . б) При каком значении числа k получится наибольшее значение числа
. б) При каком значении числа k получится наибольшее значение числа  ? в) Найдите сумму чисел во второй строке составленной таблицы. г) Отметьте на координатной плоскости точки (k;
? в) Найдите сумму чисел во второй строке составленной таблицы. г) Отметьте на координатной плоскости точки (k;  ).
).
5.10 а) Проверьте, что (а + b)2 =  а2b0 +
а2b0 +  а1b1 +
а1b1 +  а0b2. б) Проверьте, что (a + b)3 =
а0b2. б) Проверьте, что (a + b)3 =  a3b0 +
a3b0 +  a2b1 +
a2b1 +  a1b2 +
a1b2 + 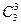 a0b3. в) Используя равенство (a + b)4 = (a + b)3(a+b), выведите формулу сокращенного умножения для суммы двух чисел в четвертой степени. г) Проверьте, что (a + b)4 =
a0b3. в) Используя равенство (a + b)4 = (a + b)3(a+b), выведите формулу сокращенного умножения для суммы двух чисел в четвертой степени. г) Проверьте, что (a + b)4 =  a4b0 +
a4b0 +  a3b1 +
a3b1 +  a2b2 +
a2b2 +  a1b3 +
a1b3 +  a0b4.
a0b4.
Повышенный уровень
Задание 1. Вычислите: а)  , б)
, б)  . (п – номер варианта)
. (п – номер варианта)
Задание 2. Вычислите а)  , б)
, б)  , в)
, в) 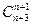 . (п – номер варианта)
. (п – номер варианта)
Задание 3. Решите задачу:
3.1 Современные пятиборцы в течение двух дней участвуют в соревновании по следующим видам спорта: конкур (кросс на лошадях), фехтование, плавание, стрельба, бег.
а) Сколько существует вариантов порядка прохождения видов соревнования?
б) Сколько существует вариантов порядка прохождения видов соревнования, если известно, что последним видом должен быть бег?
в) Сколько существует вариантов порядка прохождения видов соревнования, если известно, что последним видом должен быть бег, а первым – конкур?
г) Сколько существует вариантов, в которых конкур и фехтование не проходят подряд?
3.2 Шесть граней игрального кубика помечены цифрами 1, 2, 3, 4, 5, 6. Кубик бросают дважды и записывают выпадающие цифры.
а) Найдите число всех возможных вариантов.
б) Укажите те из них, в которых произведение выпавших чисел кратно 10.
в) Составьте таблицу из двух строк. В первой строке запишите суммы выпавших очков, во второй – количество вариантов, в которых выпадает эта сумма.
г) Составьте аналогичную таблицу для модуля разности выпавших очков.
3.3 На плоскости даны 10 точек, никакие три из которых не лежат на одной прямой. Три точки покрасили в рыжий цвет, а остальные – в черный.
а) Сколько можно провести отрезков с разноцветными концами?
б) Сколько можно провести отрезков с рыжими концами?
в) Составьте таблицу из двух строк. В первой строке запишите количество рыжих точек из 10 данных (от 0 до 10), во второй – число отрезков с разноцветными концами при таком способе раскраски.
г) 5 точек покрасили в серый цвет, 2 точки – в бурый и 3 – в малиновый цвет. Сколько можно построить серо-буро-малиновых треугольников?
3.4 Группа туристов планирует осуществить поход по маршруту Антоново – Борисово – Власово – Грибово. Из Антонова в Борисово можно сплавиться по реке или дойти пешком. Из Борисова во Власово можно дойти пешком или доехать на велосипедах. Из Власова в Грибово можно доплыть по реке, доехать на велосипедах или дойти пешком.
а) Нарисуйте дерево возможных вариантов похода.
б) Сколько всего вариантов похода могут выбрать туристы?
в) Сколько есть полностью не пеших вариантов?
г) Сколько вариантов похода могут выбрать туристы при условии, что хотя бы на одном из участков маршрута они должны использовать велосипеды?
3.5 Вова услышал в песне, что «...у зим бывают имена...». Он вспомнил семь самых хороших зим своей жизни, написал семь женских имен и решил дать каждой вспомнившейся зиме женское имя из своего списка (всем – разное).
а) Сколькими способами он может это сделать?
б) Сколько способов существует, если первая зима – точно Татьяна, а последняя – несомненно, Анна?
в) Сколько способов существует, если женских имен восемь, а не семь?
г) Сколько способов существует, если имен семь, а зим восемь?
Задание 4. Выполните требуемое действие:
4.1 Вычислите: а) 7!; б) 8!; в) 6! - 5!; г)  ; д)
; д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
4.2 Сократите дробь: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
4.3 Упростите выражение: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
4.4 Решите уравнение: а) п! = 7(п - 1)!; б) (m + 17)! = 420(m + 15)!; в) (b - 10)! = 77(b - 11)!; г) (З х)! = 504(3 x - 3)!.
4.5 1) Делится ли 11! на: а) 64; б) 25; в) 81; г) 49? 2) Сколькими нулями оканчивается число: а) 101; б) 12!; в) 15!; г) 26!?
Задание 5. Решите задачу:
5.1 а) Вычислите  для п = 3, 4, 5, 6, 7. б) Отметьте на координатной плоскости точки (п;
для п = 3, 4, 5, 6, 7. б) Отметьте на координатной плоскости точки (п;  ) для п = 3, 4, 5, 6, 7. в) На графике какой функции у = f(х) лежат все точки вида (п;
) для п = 3, 4, 5, 6, 7. в) На графике какой функции у = f(х) лежат все точки вида (п;  )? г) Начиная с какого п все эти точки будут расположены выше прямой у = 10x + 37?
)? г) Начиная с какого п все эти точки будут расположены выше прямой у = 10x + 37?
5.2 Решите уравнение: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
5.3 В чемпионате России по футболу в высшей лиге участвуют 16 команд. Перед началом чемпионата газета «Спорт» провела Интернет-опрос читателей, задав им два вопроса: 1) какая команда получит золотые, какая – серебряные и какая – бронзовые медали? 2) какие две команды окажутся среди неудачников, т. е. займут два последних места? Читатели в своих ответах указали все возможные варианты и при ответе на первый, и при ответе на второй вопросы.
а) Сколько вариантов состава неудачников указали участники опроса?
б) Сколько из них тех, в которые входит команда «Динамо»?
в) Сколько вариантов тройки призеров указали участники опроса?
г) Сколько из них тех, в которые входят «Спартак» и «Зенит»?
5.4 Из 20 вопросов к экзамену Вова 12 вопросов выучил, 5 совсем не смотрел, а в остальных что-то знает, а что-то нет. На экзамене в билете будет три вопроса.
а) Сколько существует вариантов билетов?
б) Сколько из них тех, в которых Вова знает все вопросы?
в) Сколько из них тех, в которых есть вопросы всех трех типов?
г) Сколько из них тех, в которых Вова выучил большинство вопросов?
5.5 Двенадцать рабочих надо разбить на три бригады по 4 человека.
а) Сколько может быть различных составов бригад?
б) Сколько из них тех, в которых рабочие А, Б, В окажутся вместе?
в) Сколько из них тех, в которых рабочие Д и Е окажутся вместе?
г) Сколько из них тех, в которых рабочие А, Б, В по одному окажутся в разных бригадах?
Тема 5: Элементы теории вероятностей
Основной уровень
Задание 1. Охарактеризуйте событие, о котором идет речь, как достоверное, невозможное или случайное:
1.1 А = «день рождения моего друга – число, меньше, чем 32».
1.2 А = «на уроке математики ученики делали физические упражнения».
1.3 А = «на уроке математики ученики решали математические задачи».
1.4 А = «сборная России по футболу станет чемпионом мира в 2030 году».
1.5 А = «сборная России по хоккею станет чемпионом мира в 2030 году».
1.6 А = «из интервала (1; 2) наугад взяли какое-то число, оно оказалось натуральным».
1.7 А = «из отрезка [1; 2] наугад взяли какое-то число, оно оказалось натуральным».
1.8 А = «из отрезка [1; 2] наугад взяли какое-то число, оно оказалось рациональным».
1.9 А = «вверх подкинули монету, и она упала на землю «орлом»».
1.10 А = «вверх подкинули монету, и она упала на ровную землю, встав на ребро».
Задание 2. Решите задачу используя определение классической вероятности случайного события:
2.1 Случайным образом выбрали двузначное положительное число. Найдите вероятность того, что оно оканчивается нулем.
2.2 Случайным образом выбрали двузначное положительное число. Найдите вероятность того, что оно состоит из одинаковых цифр.
2.3 Случайным образом выбрали двузначное положительное число. Найдите вероятность того, что оно больше 27 и меньше 46.
2.4 Случайным образом выбрали двузначное число. Найдите вероятность того, что оно не является квадратом целого числа.
2.5 Случайным образом выбрали двузначное число. Найдите вероятность того, что оно является квадратом целого числа.
2.6 Двузначное число составили из цифр 0, 1, 2, 3, 4. Какова вероятность того, что это число четное?
2.7 Двузначное число составили из цифр 0, 1, 2, 3, 4. Какова вероятность того, что это число нечетное?
2.8 Двузначное число составили из цифр 0, 1, 2, 3, 4. Какова вероятность того, что это число делится на 5?
2.9 Двузначное число составили из цифр 0, 1, 2, 3, 4. Какова вероятность того, что это число делится на 4?
2.10 Двузначное число составили из цифр 0, 1, 2, 3, 4. Какова вероятность того, что это число делится на 10?
Задание 3. Решите задачу, используя понятие противоположных событий:
3.1. Случайным образом выбрали целое число из промежутка [100; 200). Найдите вероятность того, что оно не оканчивается нулем.
3.2. Случайным образом выбрали целое число из промежутка [100; 200). Найдите вероятность того, что среди его цифр есть хотя бы одна цифра больше 2.
3.3. Случайным образом выбрали целое число из промежутка [100; 200). Найдите вероятность того, что оно не является квадратом целого числа.
3.4. Случайным образом выбрали целое число из промежутка [100; 200). Найдите вероятность того, что сумма его цифр меньше 17.
3.5. Случайным образом выбрали целое число из промежутка [100; 200). Найдите вероятность того, что оно не оканчивается единицей.
3.6. Игральную кость бросили дважды. Найдите вероятность того, что среди выпавших очков есть хотя бы одна единица.
3.7. Игральную кость бросили дважды. Найдите вероятность того, что сумма выпавших очков больше трех.
3.8. Игральную кость бросили дважды. Найдите вероятность того, что сумма выпавших очков меньше 11.
3.9. Игральную кость бросили дважды. Найдите вероятность того, что произведение выпавших очков меньше 27.
3.10. Игральную кость бросили дважды. Найдите вероятность того, что произведение выпавших очков меньше 15.
Задание 4. Решите задачу, используя теоремы сложения и умножения вероятностей:
4.1 В темном ящике 5 выигрышных билетов и 4 проигрышных. Вы случайно вытаскиваете 3 билета. Найдите вероятность того, что есть хотя бы один выигрышный билет.
4.2 В темном ящике 5 выигрышных билетов и 4 проигрышных. Вы случайно вытаскиваете 3 билета. Найдите вероятность того, что все билеты выигрышные.
4.3 В темном ящике 5 выигрышных билетов и 4 проигрышных. Вы случайно вытаскиваете 3 билета. Найдите вероятность того, что есть ровно один проигрышный билет.
4.4 В темном ящике 5 выигрышных билетов и 4 проигрышных. Вы случайно вытаскиваете 3 билета. Найдите вероятность того, что есть ровно два выигрышных билета.
4.5 Из колоды в 36 карт случайным образом одновременно вытаскивают 2 карты. Найдите вероятность того, что обе они черной масти.
4.6 Из колоды в 36 карт случайным образом одновременно вытаскивают 2 карты. Найдите вероятность того, что обе они пиковой масти.
4.7 Из колоды в 36 карт случайным образом одновременно вытаскивают 2 карты. Найдите вероятность того, что обе они трефовой масти.
4.8 Из колоды в 36 карт случайным образом одновременно вытаскивают 2 карты. Найдите вероятность того, что одна из них пиковой, а другая трефовой масти.
4.9 Карточка «Спортлото» содержит 49 чисел. В итоге тиража выиграют какие-то 6 чисел. Какова вероятность того, что на вашей карточке, где отмечены 6 чисел, верно угадано 0 чисел?
4.10 Карточка «Спортлото» содержит 49 чисел. В итоге тиража выиграют какие-то 6 чисел. Какова вероятность того, что на вашей карточке, где отмечены 6 чисел, верно угадано 1 число?
Задание 5. Решите задачу, используя понятие условной вероятности события:
5.1 Из колоды карт (36 карт) случайным образом поочередно вытащили две карты. Найдите вероятность того, что обе карты – тузы черной масти.
5.2 Из колоды карт (36 карт) случайным образом поочередно вытащили две карты. Найдите вероятность того, что вторая карта – пиковый туз, если первая карта – туз красной масти.
5.3 Из колоды карт (36 карт) случайным образом поочередно вытащили две карты. Найдите вероятность того, что вторая карта – красной масти, если первая карта – туз красной масти.
5.4 Из колоды карт (36 карт) случайным образом поочередно вытащили две карты. Найдите вероятность того, что вторым вынут бубновый туз, если первая карта – не бубновый туз.
5.5 В коробке «Ассорти» – 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять две конфеты. Какова.вероятность того, что конфеты – с разными начинками?
5.6 В коробке «Ассорти» – 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять две конфеты. Какова.вероятность того, что обе конфеты окажутся с любимой Таниной начинкой – шоколадной?
5.7 В коробке «Ассорти» – 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять две конфеты. Какова.вероятность того, что обе конфеты – с фруктовой начинкой?
5.8 В коробке «Ассорти» – 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять две конфеты. Какова.вероятность того, что первая конфета – с шоколадной начинкой, а вторая – с фруктовой?
5.9 В коробке «Ассорти» – 20 неразличимых по виду конфет, из которых 12 с шоколадной начинкой и 8 с фруктовой начинкой. Тане разрешили взять две конфеты. Какова.вероятность того, что первая конфета – с фруктовой начинкой, а вторая – с шоколадной?
5.10 Из колоды карт (36 карт) случайным образом поочередно вытащили две карты. Найдите вероятность того, что вторым вынут бубновый валет, если первая карта – валет черной масти.
Повышенный уровень
Задание 1. Охарактеризуйте событие, о котором идет речь, как достоверное, невозможное или случайное.
1.1 Вы открыли эту книгу на любой странице и прочитали первое попавшееся существительное. Оказалось, что: а) в написании выбранного слова есть гласная буква; б) в написании выбранного слова есть буква «о»; в) в написании выбранного слова нет гласных букв; г) в написании выбранного слова есть мягкий знак.
1.2 Даны два интервала (0; 1) и (5; 10). Из первого интервала выбрали число а, из второго — число с. Оказалось, что: а) число а меньше числа с; б) число а больше числа с; в) число а + с принадлежит интервалу (5; 10); г) число а + с не принадлежит интервалу (5; 10).
1.3 В мешке лежат 10 шаров: 3 синих, 3 белых и 4 красных. Оказалось, что: а) из мешка вынули 4 шара, и все они синие; б) из мешка вынули 4 шара, и все они красные; в) из мешка вынули 4 шара, и все они оказались разного цвета; г) из мешка вынули 4 шара, и среди них не оказалось шара черного цвета.
1.4 В двух урнах находятся по пять шаров пяти различных цветов: белого, синего, красного, желтого, зеленого. Из каждой урны






