Гистограммы особенно незаменимы в случаях, когда ряд данных состоит из очень большого количества чисел (сотни, тысячи и т. п.). В этих случаях обработчику информации в первую очередь следует разумно выбрать шаг деления промежутка между наименьшей и наибольшей вариантами. Слишком маленький шаг даст слишком большое число участков и не упростит вычисления. Слишком большой шаг приведет к слишком серьезному искажению первоначальных данных. Так, если в разобранном выше примере в качестве шага взять 10, то вся гистограмма будет состоять из горизонтального отрезка на единичной высоте, т. е. информация будет утеряна. Идеальный случай, когда шаг вам уже кто-то заранее сообщил: учитель, учебник, руководитель, заказчик и т. п.
Если ширина столбцов гистограммы достаточно мала, а основания столбцов в объединении дают некоторый промежуток, то сама гистограмма похожа на график некоторой непрерывной функции, заданной на этом промежутке. Иногда такую функцию прямо и называют выравнивающей функцией. Например, слева приведена гистограмма роста женщин, построенная по выборке, в которой было 1375 женщин.
Рисунок 6.7
Приведем пример из военного дела. Произвели 500 измерений боковой ошибки при стрельбе с самолета. На графике по оси абсцисс отложены величины ошибок («левее или правее» цели), а по оси ординат отложены частоты этих ошибок.
Рисунок 6.8
Пример из биологии: измерялся размер 12000 бобов. По оси абсцисс откладывались величины отклонений от среднего размера бобов, а по оси ординат соответствующие частоты.
Рисунок 6.9
Примеры взяты совершенно из различных областей, а графики функций, выравнивающих гистограммы, похожи друг на друга. Оказывается, что такому же закону распределения подчиняется распределение и горошин по размеру, и новорожденных младенцев по весу, и частиц газа по скоростям движения, и огромное количество других явлений окружающего нас мира. Подобно тому, как графики всех парабол получаются с помощью преобразований из одной-единственной параболы у = х2, так и все эти кривые распределения получаются из одной-единственной кривой. Ее называют кривой нормального распределения или, в честь немецкого математика Карла Гаусса, гауссовой кривой – она изображена на рисунке 6.10:
Эта «колоколообразная» кривая симметрична относительно оси ординат и имеет единственный максимум. Площадь части плоскости, ограниченной гауссовой кривой и осью Ох,равна единице. Ее «ветви» очень быстро приближаются к оси абсцисс: если найти площадь «под гауссовой кривой» на отрезке [-3; 3], то получится более 0,99, т. е. больше 99% всей площади. Для гауссовой кривой выбрано специальное обозначение у = φ(х). Аналитически она задается весьма сложно: 
.
Рисунок 6.10
Здесь, кроме знаменитого числа 
, используется не менее знаменитое число е, которое является основанием натурального логарифма; е ≈ 2,7.
Для практического использования приведенная «страшная» формула не нужна. Для значений этой функции составлены подробные числовые таблицы.
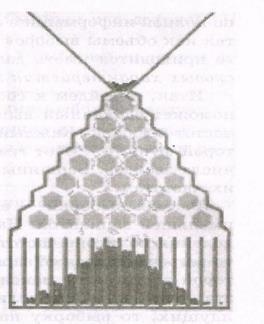
Для наглядной демонстрации нормального (гауссова) закона распределения иногда используют специальное устройство, названное по имени его изобретателя доской Гальтона (рис. 6.11). В нем падающие сверху шарики распределяются между правильными шестиугольниками и в результате попадают на горизонтальную поверхность, образуя картинку, похожую на «подграфик» гауссовой кривой.
Рисунок 6.11
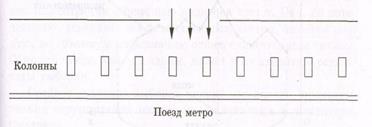Вот еще одна иллюстрация нормального закона распределения. Пассажиры метро бегут по переходу, выходящему на середину станции. Бегут они на поезд, стоящий напротив выхода из перехода. Платформа, у которой стоит поезд, равномерно разделена колоннами (рис. 6.12).
Рисунок 6.12
Ясно, что большинство пассажиров войдет в средние вагоны, а по мере удаления вагонов от центра количество садящихся в них людей будет уменьшаться. Распределение пассажиров по вагонам снова напоминает нормальное, или гауссово, распределение.
6.5 Числовые характеристики или «паспорт» выборки
Вернемся к выборкам и рядам данных. У каждой выборки есть своего рода «паспортные данные», которые весьма существенны. Следует только точно понимать, что они в принципе не могут дать полной информации о выборке: абсолютно полной информацией о выборке является сама выборка. Но так как объемы выборок данных, как правило, очень велики, то приходится иметь дело с некоторым набором важных числовых характеристик этих выборок.
Итак, перейдем к составлению «паспорта» выборки. Нам поможет сделанный выше переход от выборок к полигонам частот выборок. Каждый полигон частот – это график некоторой функции. Этот график является ломаной из конечного числа звеньев. Вершины ломаной соответствуют вариантам и их частотам.
Рисунок 6.13
Размах выборки – это разница между наибольшей и наименьшей вариантой. На графике – это длина области определения полигона частот. Мода выборки – это наиболее часто встречающаяся ее варианта. На графике – это точка, в которой достигается максимум полигона частот (рис. 6.13). Если эта точка одна или если таких точек несколько, но подряд идущих, то выборку называют унимодальной (одна мода). Возможны и бимодальные (две моды) выборки и так далее.
Рисунок 6.14
Наиболее важной характеристикой выборки является ее среднее значение или математическое ожидание описываемой случайной величины.
Для нахождения среднего значения выборки следует:
