Условие задачи
 Рис. 6.3. Условие задачи № 34:
а – сжатый стержень;
б – поперечное сечение стержня
Рис. 6.3. Условие задачи № 34:
а – сжатый стержень;
б – поперечное сечение стержня
|
Стержень, показанный на рис. 6.3, а, загружен сжимающей силой F. Поперечное сечение стержня, состоящее из двух швеллеров № 30 и двух планок, соединенных со швеллерами четырьмя болтами, изображено на рис. 6.3, б. Размер планок 400´12 мм, диаметр болтов 20 мм. Материал – сталь С235 с  . Требуется:
. Требуется:
1) найти значение критической нагрузки;
2) определить допускаемую нагрузку так, чтобы выполнялись условия устойчивости и прочности стержня;
3) вычислить нормируемый коэффициент запаса устойчивости.
Решение
Прежде всего найдем моменты инерции поперечного сечения относительно главных центральных осей. Сечение имеет две оси симметрии (оси y и z на рис. 6.3, б), поэтому эти оси и будут главными центральными осями инерции сечения. Моменты инерции относительно этих осей определяем, используя данные из сортамента прокатной стали и формулы (5.16), (5.17):

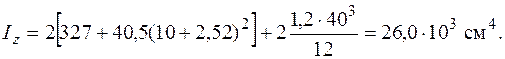
Минимальным оказался момент инерции относительно оси z. Определяем площадь сечения
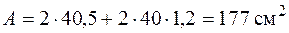
и минимальный радиус инерции по формуле (5.10)
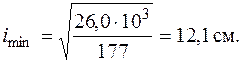
Теперь можно найти гибкость стержня. Для заданного условия закрепления стержня в соответствии с рис. 6.2, б коэффициент  . Тогда по формуле (6.1)
. Тогда по формуле (6.1)


Сравним величину полученной гибкости стержня с характеристиками  и
и  для стали С235. По формуле (6.5)
для стали С235. По формуле (6.5)
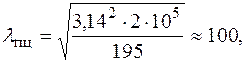
 по таблице, приведенной в [4, с. 29],. Таким образом,
по таблице, приведенной в [4, с. 29],. Таким образом,  и для определения критической силы следует использовать формулу Ясинского (6.3):
и для определения критической силы следует использовать формулу Ясинского (6.3):

Значения коэффициентов a и b в формуле Ясинского взяты из таблицы на с. 29 [4] и переведены из МПа в кН/см2.
Найдем допускаемую нагрузку из условия устойчивости по формуле (6.7). Для определения коэффициента  используем таблицу на с. 370 [2][16]. Интерполируем значения
используем таблицу на с. 370 [2][16]. Интерполируем значения 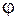 , заданные в таблице:
, заданные в таблице:  соответствует
соответствует  , а
, а  –
–  . Тогда гибкости
. Тогда гибкости  рассматриваемого стержня соответствует
рассматриваемого стержня соответствует  . Значение допускаемой нагрузки
. Значение допускаемой нагрузки

Проверим, удовлетворяет ли найденная допускаемая нагрузка условию прочности (6.8). Вычислим площадь нетто, уменьшив полную площадь сечения на площадь, занимаемую четырьмя отверстиями под болты[17]:

Тогда условие прочности

выполняется.
В заключение найдем нормируемый коэффициент запаса устойчивости по формуле (6.9):

Коэффициент запаса устойчивости находится в пределах  .
.
ПОДБОР СЕЧЕНИЯ ЦЕНТРАЛЬНО-СЖАТОГО СТЕРЖНЯ (ЗАДАЧА № 35)
 Рис. 6.4. К решению примера 1:
а – сжатый стержень;
б – поперечное сечение стержня
Рис. 6.4. К решению примера 1:
а – сжатый стержень;
б – поперечное сечение стержня
|
Пример 1
Условие задачи
Стержень, показанный на рис. 6.4, а,сжимается силой F = 600 кН. Сечение стержня, состоящее из двух равнополочных уголков, изображено на рис. 6.4, б. Материал стержня – сталь С235. Требуется подобрать размеры уголков так, чтобы выполнялись условия устойчивости и прочности и расход материала был минимальным. Ослабления составляют 15% площади сечения.
Решение
Сечение стержня состоит из уголков (прокатного профиля), поэтому используем для подбора сечения метод последовательных попыток. Поскольку в условии устойчивости имеем сразу две неизвестные величины (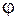 и
и  ), то одной из них задаемся произвольно. Удобно задаться
), то одной из них задаемся произвольно. Удобно задаться  . Тогда из условия устойчивости (6.6) найдем
. Тогда из условия устойчивости (6.6) найдем
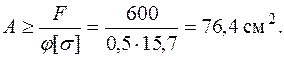
Площадь одного уголка  Из сортамента прокатной стали выбираем уголок, удовлетворяющий этому условию. Отметим, что в сортаменте может быть несколько уголков с примерно одинаковой площадью: уголки с длинной полкой и тонкой стенкой и уголки с короткой, но более толстой стенкой. Выбирать следует самые тонкие уголки, так как при одинаковой площади радиус инерции у тонких уголков больше и, следовательно, гибкость стержня с сечением из тонкого уголка меньше, а чем меньше гибкость, тем более устойчив стержень. В рассматриваемом примере выберем уголок 180´11, площадь которого
Из сортамента прокатной стали выбираем уголок, удовлетворяющий этому условию. Отметим, что в сортаменте может быть несколько уголков с примерно одинаковой площадью: уголки с длинной полкой и тонкой стенкой и уголки с короткой, но более толстой стенкой. Выбирать следует самые тонкие уголки, так как при одинаковой площади радиус инерции у тонких уголков больше и, следовательно, гибкость стержня с сечением из тонкого уголка меньше, а чем меньше гибкость, тем более устойчив стержень. В рассматриваемом примере выберем уголок 180´11, площадь которого  . Найдем радиусы инерции относительно главных центральных осей y и z, которыми являются оси симметрии сечения (см. рис. 6.4, б). Следует ожидать, что радиус инерции относительно оси y будет минимальным, так как материал ближе расположен к оси y, чем к оси z. Убедимся в этом.
. Найдем радиусы инерции относительно главных центральных осей y и z, которыми являются оси симметрии сечения (см. рис. 6.4, б). Следует ожидать, что радиус инерции относительно оси y будет минимальным, так как материал ближе расположен к оси y, чем к оси z. Убедимся в этом.


Радиус инерции одного уголка относительно оси  берем из сортамента:
берем из сортамента:  , а расстояние а (см. рис. 6.4, б) сосчитаем:
, а расстояние а (см. рис. 6.4, б) сосчитаем:

Таким образом, очевидно, что

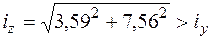
и
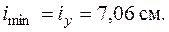
Теперь найдем гибкость стержня[18]

и из таблицы, интерполируя, найдем  . Проверим условие устойчивости:
. Проверим условие устойчивости:

Условие устойчивости выполняется, но сечение не является экономичным, поэтому сделаем еще попытку. Уменьшим размеры сечения и примем самый тонкий уголок их тех, у которых длина полки 160 мм, а именно, уголок 160´10.  ,
, 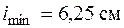 и гибкость стержня
и гибкость стержня
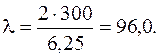
По таблице находим  и видим, что условие устойчивости выполняется с небольшим запасом:
и видим, что условие устойчивости выполняется с небольшим запасом:

Сечение из двух уголков 160´10 можно считать экономичным[19]. Условие прочности для подобранного сечения тоже выполняется, поскольку согласно условию  .
.
В заключение найдем действительный коэффициент запаса устойчивости. Поскольку стержень с подобранным сечением из уголков 160´10 имеет гибкость  , находящуюся в пределах между
, находящуюся в пределах между  и
и 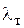 , то определяем критическую силу по формуле Ясинского:
, то определяем критическую силу по формуле Ясинского:
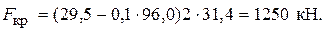
Действительный коэффициент запаса устойчивости

Пример 2
Условие задачи
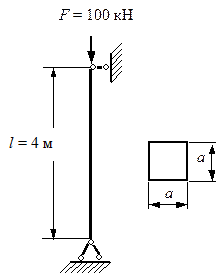 Рис. 6.5. Сжатый стержень
квадратного поперечного
сечения
Рис. 6.5. Сжатый стержень
квадратного поперечного
сечения
|
Деревянная стойка длиной l = 4 м квадратного поперечного сечения сжимается силой F = 100 кН (рис. 6.5). Требуется подобрать размер стороны квадрата а так, чтобы выполнялись условия устойчивости и прочности и расход материала был минимальным. Ослабления составляют 15 % площади сечения. Примем допускаемое напряжение на сжатие для дерева 
Решение
Поскольку размеры сечения могут быть любыми, используем метод последовательных приближений. Выполним первое приближение. Примем  . Из условия устойчивости (6.6) найдем площадь сечения, подставив
. Из условия устойчивости (6.6) найдем площадь сечения, подставив  :
:
 .
.
Поскольку  , то
, то  . Найдем минимальный радиус инерции сечения. Для квадрата любая ось является главной и радиус инерции относительно любой оси
. Найдем минимальный радиус инерции сечения. Для квадрата любая ось является главной и радиус инерции относительно любой оси
 .
.
Зная радиус инерции, вычислим гибкость стержня по формуле (6.1):
 .
.
По таблице находим для дерева 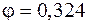 . Полученное значение
. Полученное значение 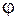 еще сильно отличатся от величины
еще сильно отличатся от величины  , принятой в начале первого приближения, поэтому выполним второе приближение. Найдем
, принятой в начале первого приближения, поэтому выполним второе приближение. Найдем 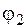 как среднее арифметическое между
как среднее арифметическое между 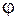 и
и  :
:

и повторим все действия, выполненные в первом приближении:
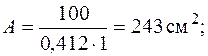
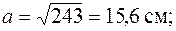
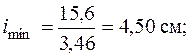

Этой гибкости соответствует  . Выполним еще одно, третье, приближение:
. Выполним еще одно, третье, приближение:



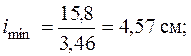

Соответствующее этой гибкости значение  отличается от
отличается от  на 1,2 %. Такая точность достаточна, поэтому примем
на 1,2 %. Такая точность достаточна, поэтому примем  . Для этого размера в условии устойчивости
. Для этого размера в условии устойчивости
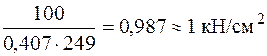
достигнуто желаемое равенство.
В заключение проверим условие прочности, считая  .
.
 .
.






