Основные определения
Внецентренное растяжение-сжатие – такой вид деформации, при котором стержень загружен растягивающими и (или) сжимающими силами, приложенными вне центра тяжести поперечного сечения. При внецентренном растяжении-сжатии стержней (рис. 5.9) в стержне возникают три внутренних усилия: продольная сила ( ) и два изгибающих момента (
) и два изгибающих момента ( и
и  ). Предполагается, что стержень имеет большую жесткость, т. е. его длина не слишком велика по сравнению с размерами поперечного сечения. В этом случае определение усилий производим по недеформированному состоянию, т. е. при определении усилий не учитываем искривление оси стержня в результате изгиба. Используя правило знаков для изгибающих моментов, описанное во вступительной части разд. 5 "Сложное сопротивление", найдем внутренние усилия как сумму усилий от каждой силы. Тогда для стержня, показанного на рис. 5.9, согласно методу сечений получим
). Предполагается, что стержень имеет большую жесткость, т. е. его длина не слишком велика по сравнению с размерами поперечного сечения. В этом случае определение усилий производим по недеформированному состоянию, т. е. при определении усилий не учитываем искривление оси стержня в результате изгиба. Используя правило знаков для изгибающих моментов, описанное во вступительной части разд. 5 "Сложное сопротивление", найдем внутренние усилия как сумму усилий от каждой силы. Тогда для стержня, показанного на рис. 5.9, согласно методу сечений получим
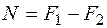 ;
;
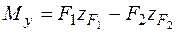 ;
;
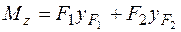 .
.
Здесь 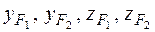 – эксцентриситеты точек приложения сил, т. е. расстояния от сил до осей
– эксцентриситеты точек приложения сил, т. е. расстояния от сил до осей 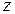 и
и  (всегда положительны);
(всегда положительны); 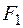 и
и 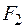 – величины сил тоже считаются положительными. Знаки в формулах для
– величины сил тоже считаются положительными. Знаки в формулах для  и
и  соответствуют правилу знаков для изгибающих моментов. Поясним их. Относительно оси
соответствуют правилу знаков для изгибающих моментов. Поясним их. Относительно оси  сила
сила 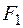 вызывает изгиб стержня выпуклостью справа. Вся область сечения, расположенная справа от оси
вызывает изгиб стержня выпуклостью справа. Вся область сечения, расположенная справа от оси  , в том числе и первый (положительный) квадрант, окажется растянутой, поэтому эта сила создает положительный изгибающий момент. Сила
, в том числе и первый (положительный) квадрант, окажется растянутой, поэтому эта сила создает положительный изгибающий момент. Сила 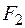 вызывает изгиб стержня относительно оси
вызывает изгиб стержня относительно оси  тоже выпуклостью справа, поэтому знак изгибающего момента
тоже выпуклостью справа, поэтому знак изгибающего момента  от силы
от силы 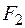 опять положительный. При изгибе относительно оси
опять положительный. При изгибе относительно оси  передняя и задняя части сечения имеют напряжения разного знака. Сила
передняя и задняя части сечения имеют напряжения разного знака. Сила 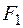 вызывает изгиб стержня выпуклостью за осью
вызывает изгиб стержня выпуклостью за осью  , т. е. задняя часть сечения (а значит, и первый квадрант) окажется растянутой, поэтому
, т. е. задняя часть сечения (а значит, и первый квадрант) окажется растянутой, поэтому  от силы
от силы 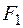 имеет знак плюс. Сила
имеет знак плюс. Сила 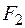 вызывает сжатие задней части сечения стержня, первый квадрант окажется сжатым, и знак изгибающего момента
вызывает сжатие задней части сечения стержня, первый квадрант окажется сжатым, и знак изгибающего момента  от
от 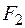 отрицательный[7].
отрицательный[7].
 Рис. 5.9. Внецентренное растяжение- сжатие жесткого стержня
Рис. 5.9. Внецентренное растяжение- сжатие жесткого стержня
|
От найденных усилий в стержне возникают только нормальные напряжения, которые определяются по формуле (5.1). Для проверки прочности стержня необходимо найти максимальные напряжения. Определение этих напряжений производится по схеме, описанной ранее, т. е.:
· строим нейтральную линию по уравнению (5.2);
· находим положение опасных точек;
· подставляя в (5.1) координаты опасных точек, вычисляем напряжения в этих точках;
· для проверки прочности сравниваем максимальные напряжения с допускаемыми.
Если в сечении действует только одна сила, растягивающая или сжимающая, то формулу (5.1) можно преобразовать к такому виду:
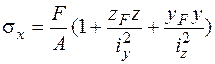 , (5.9)
, (5.9)
где
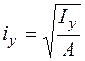 ,
, 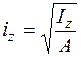 – (5.10)
– (5.10)
радиусы инерции сечения относительно главных центральных осей; 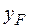 ,
, 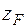 – координаты точки приложения силы;
– координаты точки приложения силы;  ,
, 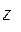 – координаты точки, в которой определяются напряжения. Все координаты вычисляются в главной центральной системе осей инерции сечения. Уравнение нейтральной линии в этом случае будет иметь вид
– координаты точки, в которой определяются напряжения. Все координаты вычисляются в главной центральной системе осей инерции сечения. Уравнение нейтральной линии в этом случае будет иметь вид
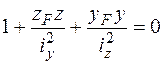 . (5.11)
. (5.11)
Используя уравнение нейтральной линии (5.11), найдем отрезки 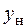 ,
, 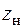 , отсекаемые нейтральной линией на осях координат (рис. 5.10),
, отсекаемые нейтральной линией на осях координат (рис. 5.10),
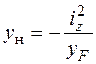 ;
; 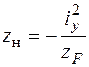 . (5.12)
. (5.12)
Откладываем эти отрезки с учетом знаков вдоль главных центральных осей и строим нейтральную линию (см. рис. 5.10).
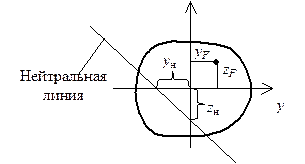 Рис. 5.10. Положение нейтральной линии
при внецентренном растяжении (сжатии)
одной силой
Рис. 5.10. Положение нейтральной линии
при внецентренном растяжении (сжатии)
одной силой
|
Из формул (5.12) следуют некоторые закономерности, связывающие положение полюса (т. е. точки приложения силы) и нейтральной линии, которые удобно использовать для анализа решения задачи. Перечислим самые важные из этих закономерностей:
1) нейтральная линия всегда расположена в квадранте, противоположном тому, в котором находится полюс (см. рис. 5.10);
2) если полюс находится на одной из главных осей, то нейтральная линия перпендикулярна этой оси;
3) если полюс приближается к центру тяжести сечения, то нейтральная линия удаляется от него;
4) если полюс движется по прямой линии, то нейтральная линия поворачивается вокруг неподвижной точки.
 Рис. 5.11. Вид эпюры напряжений:
а – для полюса, расположенного на контуре ядра сечения;
б – для полюса, находящегося внутри ядра сечения
Рис. 5.11. Вид эпюры напряжений:
а – для полюса, расположенного на контуре ядра сечения;
б – для полюса, находящегося внутри ядра сечения
|
Из предпоследней закономерности следует, что если сила приложена достаточно близко к центру тяжести, то нейтральная линия удаляется так далеко, что нигде не пересекает сечение. Это означает, что напряжения во всем сечении будут иметь один знак. Следовательно, существует такая область вокруг центра тяжести, которая обладает следующим свойством: если внутри этой области или на ее контуре приложить силу (растягивающую или сжимающую), то во всем сечении будут возникать напряжения одного знака. Такая область называется ядром сечения. Рис. 5.11 поясняет данное определение ядра сечения. Нейтральная линия касается сечения, если сила приложена на контуре ядра сечения (см. рис. 5.11, а), и нейтральная линия проходит за сечением, если полюс расположен внутри ядра сечения (см. рис. 5.11, б).
Из приведенного определения ядра сечения следует первый способ построения ядра сечения. Согласно этому способу надо обвести контур сечения нейтральными линиями, касающимися контура и нигде не пересекающими сечение. Полюсы, соответствующие этим нейтральным линиям, будут находиться на контуре ядра сечения. На практике обычно более удобным является второй способ построения ядра сечения, который основан на свойстве взаимности нейтральной линии и полюса [2, гл. 7, § 36]. Для построения ядра сечения по второму способу надо поместить полюсы во внешних всех угловых точках сечения, имеющего форму многоугольника, и построить соответствующие им нейтральные линии. Эти нейтральные линии очертят контур ядра сечения. Отметим, что при построении ядра сечения нельзя располагать полюсы во внутренних угловых точках, так как через них нельзя провести касательные, нигде не пересекающие сечение. Рис. 5.12 поясняет разницу между внешними и внутренними угловыми точками многоугольника.
Для определения напряжений и проверки прочности стержня произвольного сечения, а также для построения ядра сечения необходимо научиться находить геометрические характеристики сечений, важнейшими из которых являются моменты инерции. Этому посвящен п. 5.2.1 гл. 5.
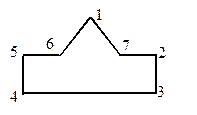 Рис. 5.12. Точки 1–5 –внешние,
6, 7 – внутренние угловые
точки
Рис. 5.12. Точки 1–5 –внешние,
6, 7 – внутренние угловые
точки
|
5.2.1. Определение моментов инерции сложных сечений относительно главных центральных осей (задачи № 29, 30, 31)
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 4.
Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977. Гл. 15.
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 5.
Основные определения
Напомним, что осевыми моментами инерции плоской фигуры относительно произвольных осей  и
и  называются величины
называются величины
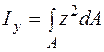 ;
; 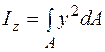 . (5.13)
. (5.13)
Центробежным моментом инерции является величина
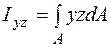 . (5.14)
. (5.14)
Оси называются центральными, если они проходят через центр тяжести фигуры, т. е. статические моменты относительно этих осей равны нулю. Главными осями инерции фигуры называются оси, относительно которых центробежный момент инерции равен нулю. Если фигура имеет хотя бы одну ось симметрии, то эта ось является главной осью.
Для вычисления моментов инерции относительно главных центральных осей надо уметь находить положение центра тяжести фигуры и знать, как изменяются моменты инерции при параллельном переносе и повороте осей. Напомним уже известные студенту формулы и приведем новые.
Определение центра тяжести фигуры производится по формулам
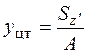 ;
; 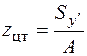 , (5.15)
, (5.15)
где вспомогательные оси  ,
, 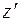 , относительно которых вычисляются статические моменты, выбираются произвольно.
, относительно которых вычисляются статические моменты, выбираются произвольно.
При параллельном переносе осей моменты инерции изменяются по следующим законам:
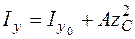 ; (5.16)
; (5.16)
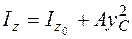 ; (5.17)
; (5.17)
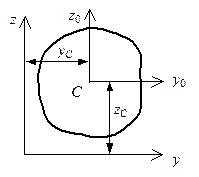 Рис. 5.13. Параллельный перенос осей
Рис. 5.13. Параллельный перенос осей
|
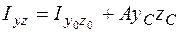 . (5.18)
. (5.18)
В формулах (5.16)–(5.18) 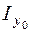 ,
, 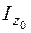 ,
, 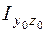 – моменты инерции относительно центральных осей;
– моменты инерции относительно центральных осей; 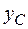 ,
, 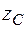 – координаты центра тяжести (точки
– координаты центра тяжести (точки  на рис. 5.13) в системе осей
на рис. 5.13) в системе осей  ,
,  , параллельных центральным осям
, параллельных центральным осям 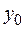 ,
,  (см. рис. 5.13). Заметим, что если при вычислении осевых моментов инерции знаки координат не имеют значения, то при определении центробежного момента инерции знаки координат
(см. рис. 5.13). Заметим, что если при вычислении осевых моментов инерции знаки координат не имеют значения, то при определении центробежного момента инерции знаки координат 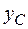 ,
, 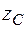 надо обязательно учитывать.
надо обязательно учитывать.
При повороте осей (рис. 5.14) координаты точки меняются по известному закону
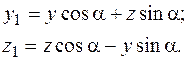 (5.19)
(5.19)
Подставляя эти формулы в (5.13)–(5.14), получим, что моменты инерции изменяются следующим образом:
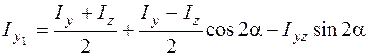 ; (5.20)
; (5.20)
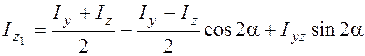 ; (5.21)
; (5.21)
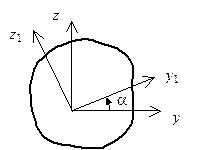 Рис. 5.14. Поворот осей
Рис. 5.14. Поворот осей
|
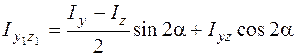 . (5.22)
. (5.22)
Угол 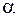 в формулах (5.20)–(5.22), на который поворачиваются оси, считается положительным, если он отсчитывается от положительного направления оси
в формулах (5.20)–(5.22), на который поворачиваются оси, считается положительным, если он отсчитывается от положительного направления оси  к положительному направлению оси
к положительному направлению оси  . На рис. 5.14 угол
. На рис. 5.14 угол 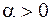 .
.
Чтобы найти, на какой угол  надо повернуть оси, чтобы они стали главными осями инерции, положим согласно определению главных осей центробежный момент инерции по (5.22) равным нулю. Тогда
надо повернуть оси, чтобы они стали главными осями инерции, положим согласно определению главных осей центробежный момент инерции по (5.22) равным нулю. Тогда
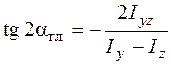 . (5.23)
. (5.23)
Подставляя найденный угол  в формулу (5.20), можно получить формулу для определения моментов инерции относительно главных осей
в формулу (5.20), можно получить формулу для определения моментов инерции относительно главных осей
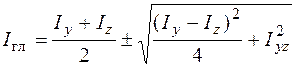 . (5.24)
. (5.24)
Моменты инерции относительно главных осей имеют экстремальные значения среди бесконечного множества центральных осей: относительно одной оси момент инерции максимален, относительно другой имеет минимальное значение. Чтобы выяснить, какой момент инерции: максимальный или минимальный – имеет место для главной оси  , повернутой на угол
, повернутой на угол  от оси
от оси  , исследуем знак второй производной функции
, исследуем знак второй производной функции  , определяемой формулой (5.20). Вычислим эту производную:
, определяемой формулой (5.20). Вычислим эту производную:
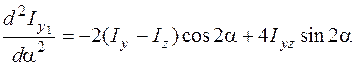 . (5.25)
. (5.25)
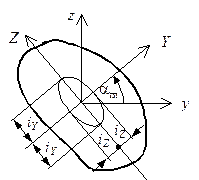 Рис. 5.15. Эллипс
инерции
Рис. 5.15. Эллипс
инерции
|
Если при 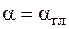 вторая производная
вторая производная 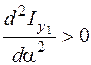 , то относительно оси
, то относительно оси  момент инерции минимален (
момент инерции минимален (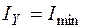 ), если
), если 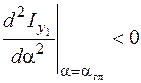 , то
, то 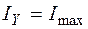 .
.
После определения моментов инерции относительно главных осей можно построить эллипс инерции – эллипс, полуоси которого равны радиусам инерции относительно главных осей. Радиус инерции  откладывается вдоль главной оси
откладывается вдоль главной оси  , а
, а 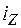 – вдоль оси
– вдоль оси  (рис. 5.15). Построение эллипса инерции удобно использовать для анализа правильности определения моментов инерции. Эллипс инерции должен быть вытянут в том направлении, в котором вытянута фигура.
(рис. 5.15). Построение эллипса инерции удобно использовать для анализа правильности определения моментов инерции. Эллипс инерции должен быть вытянут в том направлении, в котором вытянута фигура.
В заключение приведем некоторые формулы для определения моментов простых фигур относительно центральных осей. Для прямоугольника (рис. 5.16, а) оси 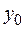 ,
,  являются не только центральными, но и главными, моменты инерции относительно этих осей
являются не только центральными, но и главными, моменты инерции относительно этих осей
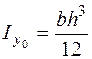 ;
; 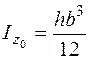 ;
; 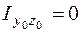 . (5.26)
. (5.26)
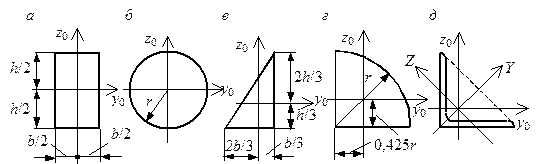 Рис. 5.16. К определению моментов инерций простых фигур
Рис. 5.16. К определению моментов инерций простых фигур
|
Для круга (рис. 5.16, б) любая ось, проходящая через центр тяжести, является главной и
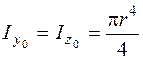 ;
; 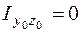 . (5.27)
. (5.27)
У прямоугольного треугольника (рис. 5.16, в) оси 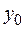 ,
,  не являются главными, поэтому центробежный момент инерции относительно этих осей не равен нулю. Моменты инерции треугольника определяются по формулам
не являются главными, поэтому центробежный момент инерции относительно этих осей не равен нулю. Моменты инерции треугольника определяются по формулам
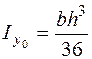 ;
; 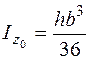 ;
; 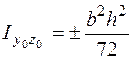 . (5.28)
. (5.28)
На рис. 5.16, г показана фигура, представляющая собой четверть круга (квадрант круга). Для этой фигуры относительно центральных осей 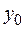 ,
,  моменты инерции
моменты инерции

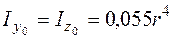 ;
; 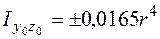 . (5.29)
. (5.29)
Чтобы определить знак центробежного момента инерции треугольника или квадранта круга, надо использовать следующее правило знаков: если гипотенуза треугольника (дуги квадранта) в системе координат 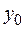 ,
,  описывается возрастающей функцией, то центробежный момент инерции положителен. Для показанного на рис. 5.16, в треугольника
описывается возрастающей функцией, то центробежный момент инерции положителен. Для показанного на рис. 5.16, в треугольника 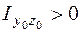 , квадрант круга, изображенный на рис. 5.16, г, имеет отрицательный центробежный момент инерции.
, квадрант круга, изображенный на рис. 5.16, г, имеет отрицательный центробежный момент инерции.
При определении моментов инерции фигуры, состоящей из прокатных профилей: двутавров, швеллеров, уголков (как в задаче № 31), осевые моменты инерции относительно собственных центральных осей двутавров, швеллеров, уголков берутся из таблиц прокатных профилей. Центробежные моменты инерции двутавров и швеллеров относительно собственных осей равны нулю. Центробежный момент инерции равнобоких уголков относительно осей  , параллельных полкам, определяется по формуле
, параллельных полкам, определяется по формуле
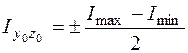 , (5.29а)
, (5.29а)
где 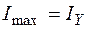 ,
, 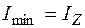 – моменты инерции относительно главных центральных осей
– моменты инерции относительно главных центральных осей  уголка (рис. 5.16, д) – находятся по таблице прокатных профилей. Выбор знака в формуле (5.29а) производится по той же схеме, что и для треугольника или квадранта круга: если линия, соединяющая крайние точки уголка (пунктир на рис. 5.16, д), описывается возрастающей функцией в системе координат
уголка (рис. 5.16, д) – находятся по таблице прокатных профилей. Выбор знака в формуле (5.29а) производится по той же схеме, что и для треугольника или квадранта круга: если линия, соединяющая крайние точки уголка (пунктир на рис. 5.16, д), описывается возрастающей функцией в системе координат  , то
, то 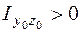 . Для уголка на рис. 5.16, д центробежный момент инерции
. Для уголка на рис. 5.16, д центробежный момент инерции 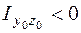 .
.
Примеры решения задач






