Основные определения
В общем случае сложного сопротивления в стержне возникают все шесть видов внутренних усилий одновременно. Эти шесть усилий определяем, как обычно, методом сечений и строим эпюры усилий. При определении внутренних усилий используем правила знаков, описанные во вступительной части разд. 5 и поясняемые рис. 5.1. После определения внутренних усилий находим опасные сечения, а в опасных сечениях – опасные точки. Рассмотрим подробно, где расположены опасные точки в двух наиболее часто используемых сечениях: круглом и прямоугольном[10]. Выпишем формулы, необходимые для проверки прочности в этих точках.
Рис. 5.25. Изображение пар сил Мy и Мz
в виде векторов
|
Для определения положения опасных точек в круглом сечении построим эпюры распределения напряжений. Чтобы построить эпюру нормальных напряжений, вызванных двумя изгибающими моментами 
и 
, определим направление суммарного изгибающего момента. Изобразим пары 
и 
в виде векторов, определяя их направление по правилу правого винта (рис. 5.25). Полный изгибающий момент является равнодействующей этих векторов и изображен на рис. 5.26. Поскольку для круглого сечения любая ось является главной, то в какой бы плоскости ни был приложен изгибающий момент, он вызывает плоский изгиб. Нейтральная линия в этом случае перпендикулярна плоскости изгиба, то есть совпадает с линией действия вектора полного изгибающего момента 
. На рис. 5.26 показана эпюра нормальных напряжений, вызванных действием изгибающего момента . Кроме того, в сечении возникают нормальные напряжения от продольной силы N и касательные напряжения от крутящего момента 
. Эпюры распределения этих напряжений показаны на рис. 5.26[11]. Знаки напряжений соответствуют положительным значениям внутренних усилий. Видно, что опасными точками могут быть точки 1, 1¢, в которых действуют максимальные нормальные напряжения от изгиба и продольной силы и максимальные касательные напряжения, вызванные крутящим моментом. Для проверки прочности хрупких материалов важен знак нормальных напряжений (более опасной точкой будет, как правило, точка с растягивающими напряжениями), для пластичных материалов опасной будет точка, где нормальные напряжения от изгиба и продольной силы имеют одинаковые знаки. Опасные точки находятся в "балочном" напряженном состоянии, и проверку прочности в них следует осуществлять по теориям прочности, соответствующим материалу стержня. Приведем условия прочности, справедливые для "балочного" напряженного состояния, по двум наиболее часто используемым теориям:
· для хрупких материалов – теория Мора
(5.30)
где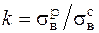 
; 
Рис. 5.26. Эпюры распределения
напряжений в стержне круглого сечения
|
· для пластичных материалов – третья теория прочности
. (5.31)
В формулах (5.30), (5.31) 
и 
– напряжения в опасных точках.
В точках 1, 1¢ круглого сечения эти напряжения определяются так:
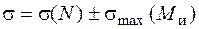; (5.32)
; (5.33)
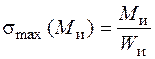; (5.34)
, (5.35)
где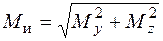 
; 
; 
; 
. Поясним выбор знака в формуле (5.32). В рассматриваемой задаче в точке 1 складываются растягивающие напряжения от изгиба и продольной силы, в точке 1’ от растягивающих напряжений, вызанных N, вычитаются сжимающие напряжения от М и.
При подборе сечения обычно пренебрегают влиянием продольной силы. В этом случае условия прочности (5.30) и (5.31) для круглого сечения с учетом формул (5.34) и (5.35) можно преобразовать. Теория Мора приобретает такой вид:
, (5.36)
а третья теория прочности приводится к следующему условию:
, (5.37)
где 
. Из условий прочности (5.36), (5.37) можно найти необходимый момент сопротивления, а далее радиус поперечного сечения. Чтобы учесть продольную силу, немного увеличивают полученное значение радиуса (как правило, достаточно округления в большую сторону), находят напряжения по формулам (5.33)–(5.35) и проверяют прочность с учетом 
по условиям (5.30) или (5.31).
Рис. 5.27. Эпюры распределения напряжений
в стержне прямоугольного сечения
|
Построим эпюры распределения напряжений от всех усилий в прямоугольном сечении и определим положение опасных точек. Эти эпюры изображены на рис. 5.27, где знаки и направления напряжений соответствуют положительным внутренним усилиям. Из рис. 5.27 следует, что в прямоугольном сечении в общем случае опасными могут быть три группы точек:
· точки 1, 1¢ с максимальными нормальными напряжениями (для хрупких материалов важна не только величина напряжения, но и его знак). Напряжения в них
; (5.38)
Согласно рис. 5.27 в точке 1 складываются растягивающие напряжения от всех усилий (М y, M z и N). В точке 1¢ от сжимающих напряжений, вызванных изгибающими моментами, вычитаются растягивающие напряжения от продольной силы.
· точки 2, 2¢ – в них действуют нормальные напряжения от , максимальные нормальные напряжения от и максимальные касательные напряжения, вызванные крутящим моментом и поперечной силой 
:
, (5.39)
; (5.40)
· точки 3, 3¢ с нормальными напряжениями от , максимальными нормальными напряжениями от и, кроме того, в этих точках действуют касательные напряжения от кручения и максимальные касательные напряжения, вызванные поперечной силой 
:
, (5.41)
. (5.42)
В зависимости от величин и знаков внутренних усилий необходимо выбрать самые опасные точки и проверить в них прочность. Знаки "плюс" или "минус" в формулах (5.38)–(5.42) выбираются в зависимости от направления напряжений в рассматриваемой точке. При этом в точках 2, 2¢ или 3, 3¢ хотя бы для одного напряжения ( или ) направления должны совпадать.
В точке 1, где нормальные напряжения от , и имеют одинаковый знак, условие прочности записывается так:
, (5.43)
так как эта точка находится в линейном напряженном состоянии. Для хрупких материалов в правой части неравенства стоит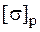 
или 
в зависимости от направления напряжения. Точки 2 (2¢) и 3 (3¢) находятся в "балочном" напряженном состоянии и условие прочности в них записывается по формулам (5.30) или (5.31) в зависимости от материала. Для хрупких материалов наиболее опасными являются точки, в которых действуют растягивающие напряжения, для пластичных материалов это точки с максимальными по модулю нормальными напряжениями.
В формулах (5.38)–(5.42)
; (5.44)
; (5.45)
; (5.46)
; (5.47)
; (5.48)
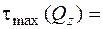
; (5.49)
; 
; 
; 
. Коэффициенты 
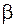и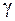 
определяются по таблице и зависят от 
. В приведенных формулах 
– меньшая сторона прямоугольника, параллельная оси 
. Знаки усилий в формулах (5.33)–(5.35) и (5.44)–(5.49) не учитываются.
Подбор размеров прямоугольного сечения производят из условия прочности в угловой точке без учета продольной силы. Перед подбором размеров сечение стержня надо расположить рационально. Если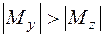 
, то наибольшая сторона 
должна быть перпендикулярна оси 
. В этом случае 
; 
. В противном случае сторона должна быть расположена параллельно оси , 
, а 
. Условие прочности (5.43) в угловой точке без учета записывается следующим образом:
. (5.50)
Зная отношение моментов сопротивления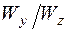 
, из (5.50) можно найти необходимую величину момента сопротивления, а далее размеры сечения. Для учета продольной силы обычно округляют полученные размеры в большую сторону и проверяют прочность во всех опасных точках прямоугольного сечения с учетом всех усилий по приведенным выше формулам.
Примеры решения задач
5.3.1. Расчет стержня в общем случае сложного
сопротивления (задача № 32)
Условие задачи
Рис. 5.28. К решению задачи № 32: а – схема стержня с нагрузками;
б – местные системы координат на участках стержня
|
Задан стержень пространственного очертания, загруженный нагрузками (рис. 5.28, а). Для заданного материала стержня требуется подобрать размеры поперечного сечения наиболее опасного участка для двух вариантов сечения: круглого и прямоугольного.
Решение
Определим внутренние усилия, используя метод сечений и правила знаков для усилий, справедливые для всех задач сложного сопротивления (см. рис. 5.1). На каждом участке введем местные системы координат, показанные на рис. 5.28, б. Ось х всегда направлена вдоль оси стержня[12], оси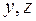 
– главные центральные оси инерции сечения. Чтобы не определять опорные реакции, будем рассматривать все силы со свободного конца стержня и найдем усилия в сечениях 0–5 (см. рис. 5.28, б).
; 
; 
;
; 
; 
;
; 
; 
; 
;
; 
; 
;
; 
;
; 
; 
;
; 
;
; 
; 
.
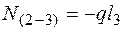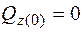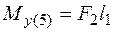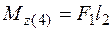В соответствии с полученными результатами построим эпюры внутренних усилий (рис. 5.29). В рассматриваемом примере опасным является участок длиной 
, где действуют все усилия. На этом участке опасным будем считать сечение 5 (хотя при определенном сочетании величин нагрузок и размеров может быть опасным и сечение 4). Считая, что материал стержня – чугун (
, 
, 
) подберем размеры поперечного сечения стержня, приняв следующие исходные данные: 
; 
; 
; 
; 
; 
. Для этих данных в опасном сечении 5 действуют такие усилия: 
, 
, 
, 
, 
, 
.
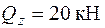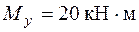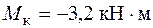Рассмотрим первый вариант – стержень круглого поперечного сечения. Подбор радиуса сечения производим без учета продольной и поперечных сил в соответствии с заданным материалом из условия прочности по теории Мора (5.36). В формуле (5.36)
, 
, 
.
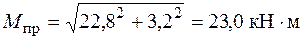Из условия (5.36) найдем необходимый момент сопротивления
см3,
откуда, вспомнив, что , найдем радиус сечения
см.
Округляя радиус в большую сторону, приме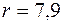м 
см.
Рис. 5.29. Эпюры внутренних усилий в стержне
|
Далее необходимо построить эпюры распределения напряжений в круглом поперечном сечении так, как описано во вступительной части разд. 5.3. Для рассматриваемого примера эти эпюры показаны на рис. 5.30. Напряжения определены по формулам (5.33)–(5.35). Сделаем проверку прочности для найденного размера с учетом продольной силы. Для чугунного стержня опасной является точка, в которой действуют растягивающие нормальные напряжения, т. е. точка 1 на рис. 5.30. В этой точке
кН/см2;
кН/см2.
Подставим найденные напряжения в условие прочности по теории Мора (5.30):
кН/см2 < 
кН/см2.
Рис. 5.30. Эпюры напряжений (в кН/см2) в стержне
круглого сечения
|
Таким образом, найденный радиус 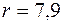см удовлетворяет условию прочности с учетом продольной силы и является окончательным.
Теперь рассмотрим второй вариант – стержень прямоугольного сечения с отношением 
. Подбор сечения производим из условия прочности (5.50) в угловой точке сечения. Поскольку в рассматриваемом примере 
, то располагаем сечение выгодным образом, т.е. так, чтобы ось располагалась по середине длинной стороны прямоугольника. Тогда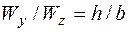 
и условие (5.50) для чугуна перепишем в таком виде:
.
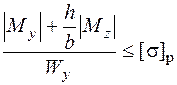Отсюда получим необходимый момент сопротивления
см3
и, учтя, что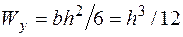 
, найдем высоту сечения
см 
см.
Построим эпюры распределения напряжений в прямоугольном сечении от всех видов внутренних усилий так, как описано во вступительной части разд. 5.3, и проверим прочность во всех опасных точках. Эпюры напряжений и опасные точки для рассматриваемого примера показаны на рис. 5.31. Напряжения найдены по формулам (5.44)–(5.49). Опасными для хрупкого материала являются точки, в которых действуют растягивающие напряжения, т. е. точки 1, 2 и 3 (см. рис. 5.31). Суммируем напряжения в опасных точках с учетом их направлений. В точке 1
кН/см2 < кН/см2,
то есть условие прочности выполняется.
В точке 2
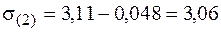кН/см2,
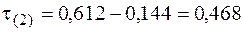кН/см2
и условие прочности (5.30) по теории Мора
< кН/см2
выполняется.
Наконец, в точке 3 действуют напряжения
кН/см2,
кН/см2.
Условие прочности (5.30) в этой точке
< кН/см2
Рис. 5.31. Эпюры напряжений (в кН/см2) в стержне
прямоугольного сечения
|
тоже выполняется. Таким образом, найденные размеры поперечного сечения 
и 
удовлетворяют условиям прочности во всех опасных точках.
5.3.2. Расчет коленчатого вала на изгиб с кручением
(задача № 33)
Рекомендуемая литература
Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995. Гл. 19 (§ 19.1–19.6).
Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989. Гл. 15.
Феодосьев В. И.. Сопротивление материалов. М.: Наука, 1970. Гл. ХIII.
Иванов М. Н. Детали машин. М.: Высшая школа, 1998. Гл. 15.
Основные определения
Коленчатый вал является плоской рамой, испытывающей действие пространственных циклических нагрузок, в которой возможно усталостное разрушение, поэтому, кроме расчета на статические нагрузки, требуется учет влияния на напряжения динамического действия нагрузок. Известно, что под действием длительных, циклически меняющихся нагрузок материалы конструкций обнаруживают значительное понижение прочности. Это явление носит название усталости материала. Способность материала сопротивляться усталостному разрушению называют выносливостью. Важной характеристикой материала является предел выносливости, определяемый экспериментально. Следует отметить, что расчет на циклические нагрузки (усталостную прочность) носит эмпирический характер, требует наличия большого количества экспериментальных данных, обычно приводимых в справочниках в виде таблиц и графиков. Используемый в рассматриваемой задаче расчет на усталостную прочность является достаточно приближенным, так как многие необходимые для расчета величины эмпирических коэффициентов принимаются условно. Более точный расчет коленчатых валов рассматривается в специальных курсах.
Один из способов расчета на усталостную прочность сводится к определению действительного коэффициента запаса усталостной прочности 
и сравнению его с нормируемым коэффициентом запаса n. В данном расчете примем 
. Условием усталостной прочности является условие
. (5.51)
Для "балочного" напряженного состояния, которое имеет место в опасных точках коленчатого вала, коэффициент запаса усталостной прочности находится по формуле Гафа и Полларда
, (5.52)
где 
– запас прочности по нормальным напряжениям в предположении, что касательные напряжения равны нулю; 
– запас прочности по касательным напряжениям, когда 
. Коэффициенты и определяются следующим образом:
; (5.53)
. (5.54)
В формулах (5.53), (5.54) 
и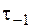 
– пределы выносливости при изгибе и кручении для симметричного цикла; 
, 
– амплитудные значения цикла напряжений при изгибе и кручении; 
, 
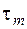– средние напряжения цикла при изгибе и кручении. Остальные величины, входящие в формулы (5.53), (5.54), являются эмпирическими коэффициентами, учитывающими:
· 
, 
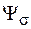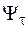– влияние среднего напряжения на величину сопротивления усталости;
· 
, 
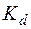– масштабный фактор и степень шероховатости поверхности;
· 
, 
– влияние концентрации напряжений на сопротивление усталости.
Эти коэффициенты в инженерных расчетах определяют по специальным справочникам. При решении рассматриваемой задачи студенты условно принимают значения этих коэффициентов по данным, приведенным в [4].
