Все вещества могут существовать в различных агрегатных состояниях или в различных модификациях одного агрегатного состояния в зависимости от условий (Т, р и т.д.). Переход вещества из одного агрегатного состояния в другое, или изменение модификации агрегатного состояния вещества называется фазовым переходом первого рода. Фазовые переходы 1-го рода сопровождаются выделением или поглощением теплоты.
Система может содержать одновременно несколько фаз. Чтобы такая система находилась в равновесии, необходимо выполнение нескольких условий, одно из них: термодинамический потенциал Гиббса G должен принимать минимальное значение.
. (25)
При динамическом равновесии выполняется уравнение:
, (26)
где g1 и g2 – удельные (относящиеся к единице массы вещества) термодинамические потенциалы 1-й и 2-й фаз.
Уравнение, связывающее между собой давление и температуру, при которых осуществляется фазовый переход первого рода, имеет вид
 - уравнение Клапейрона-Клаузиуса (27)
|
где 
- удельный объем. Две любые фазы вещества могут находиться в равновесии лишь при определенном давлении, зависящем от температуры.
Максимально возможное число фаз вещества, находящихся в равновесии друг с другом равно трем, если это изобразить на плоскости p, T, то она получится разделена на три области: твердую фазу (т), жидкую (ж) и газообразную (г), рис.20.
Границами соприкасающихся фаз являются кривые сублимации (испарение твердого тела), испарения и плавления, характеризующие двухфазные равновесные состояния.
|
 | |||
 | |||
Подобные диаграммы строят экспериментально для разных веществ, они позволяют предсказывать в каких равновесных состояниях может находиться вещество при тех или иных значениях давления и температуры, а также когда и какие оно будет испытывать фазовые превращения при том или ином процессе. Например, кривая испарения заканчивается в критической точке К, поэтому возможен непрерывный переход вещества из жидкого состояния в газообразное и обратно путем обхода точки К «сверху», в этом случае такой переход не сопровождается двухфазным состоянием.
Задачи
6.1. Получить уравнение Клапейрона-Клаузиуса методом циклов.
6.2. Вывести уравнение Клапейрона-Клаузиуса методом термодинамического потенциала.
6.3. Ромбическая сера превращается в моноклинную при 
. При атмосферном давлении удельная теплота превращения 
. Скачок удельного объема серы при фазовом превращении 
. Найти смещение 
точки фазового перехода серы при изменении давления на 
.
6.4. Кусочек льда массы 
непрерывно нагревают при атмосферном давлении от температуры 
до 
, пока все вещество не перейдет в пар. Построить график зависимости энтропии воды от абсолютной температуры 
на всем вышеуказанном интервале температур.
6.5. При стремлении температуры фазового перехода «жидкость – пар» к критической температуре Тк удельная теплота испарения (конденсации) стремится к нулю. Объяснить это свойство с помощью уравнения Клапейрона-Клаузиуса.
6.6. В закрытом сосуде с объемом 
находится 1 кг воды при температуре 
. Пространство над водой занято насыщенным водяным паром (воздух выкачан). Найти увеличение массы насыщенного пара 
при повышении температуры системы на 
. Удельная теплота парообразования 
. При расчетах пар считать идеальным газом. Удельным объемом воды пренебречь по сравнению с удельным объемом пара.
6.7 Найти зависимость давления насыщенного пара от температуры в следующих упрощающих предположениях: удельную теплоту парообразования q считать не зависящей от температуры; удельный объем жидкости пренебрежимо мал по сравнению с удельным объемом пара; к жидкости применимо уравнение состояния Клапейрона. (Эти упрощения допустимы вдали от критической температуры, если интервал изменения температур не слишком широк.)
6.8. Кусок льда помещен в адиабатическую оболочку при температуре 0˚С и атмосферном давлении. Как изменится температура льда, если его адиабатически сжать до давления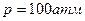 
? Какая доля льда 
при этом расплавится? Удельные объемы воды 
, льда 
. Теплоемкости воды и льда связаны соотношением 
.
Ответы
6.3. 
6.6. 
, где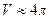 
-объем пара;
6.7. 
, где р0 – давление насыщенного пара при Т0;
6.8. 
Список литературы
1. Иродов И.Е. Задачи по общей физике. – СПб.: Лань, 2001.
2. Иродов И.Е. Физика макросистем. Основные законы. – М.: Лаборатория Базовых Знаний, 2001.
3. Кассандрова О.Н., Матвеев А.Н., Попов В.В. Методика решения задач по молекулярной физике./ Под общей ред. А.Н. Матвеева. - М.: Изд-во МГУ, 1982.
4. Кубо Риого. Термодинамика. Современный курс с задачами и решениями. – М.: Наука, 1970.
5. Матвеев А.Н. Молекулярная физика. - М.: Высш. шк., 1987.
6. Общая физика. Молекулярная физика. Определение основных характеристик фазовых переходов 1-го рода при кипении воды: Метод. указания к лабораторной работе. –Красноярск, КрасГУ, 2000.
7. Орир Дж. Физика. Т.1. – М.: Мир, 1981.
8. Сборник задач по общему курсу физики. Термодинамика и молекулярная физика. /Под ред. Д.В. Сивухина. – М.: Наука, 1976.
9. Сивухин Д.В. Общий курс физики. Т.2. – М.: Наука, 1979.
