Семинар 3. Второе начало термодинамики. Энтропия

Второе начало термодинамики имеет особый статус не только фундаментального закона физики, но и универсального принципа естествознания в целом.

Второе начало дает информацию о направлении процессов, которые могут происходить в действительности. Оно, совместно с первым началом, позволяет установить множество точных количественных соотношений между различными макроскопическими параметрами тел в состоянии термодинамического равновесия. Это оказывается возможным благодаря определению такой величины как энтропия через теплоту. Энтропия (греч. – поворот, превращение) служит мерой преобразования или эволюции системы.

Существует несколько десятков различных формулировок второго начала. В большинстве из них термин «энтропия» не используется (см. формулировки Кельвина, Клаузиуса и Оствальда).

Второе начало термодинамики
Формулировка Кельвина: Невозможен циклический процесс, единственным результатом которого является производство работы А за счет уменьшения внутренней энергии U только одного теплового резервуара (рис.13)	Формулировка Клаузиуса: Невозможен циклический процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому (рис.14)	Формулировка Оствальда: Невозможно построить «вечный двигатель второго рода».

Такие процессы невозможны. Они запрещены вторым началом.

Рис.14

Рис.13

Самая краткая и исчерпывающая формулировка второго начала – энтропия есть функция состояния системы. Все остальные формулировки являются строго логически доказуемыми следствиями этой аксиомы. Именно в этом духе сформулировал второе начало термодинамики А.Зоммерфельд в развернутой двухчастной форме.

Часть первая. Каждая термодинамическая система обладает функцией состояния, называемой энтропией. Энтропия вычисляется следующим образом. Система переводится из произвольно выбранного начального состояния в соответствующее конечное состояние через последовательность состояний равновесия. Вычисляются все подводимые при этом к системе порции тепла 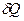, делятся каждая на соответствующую ей абсолютную температуру Т и все полученные таким образом значения суммируются.

(13)

Часть вторая. При реальных (не идеальных) процессах энтропия замкнутой системы возрастает.

Содержание второй части формулировки А.Зоммерфельда в большинстве учебников рассматривается как самодостаточная формулировка второго начала, или как закон возрастания энтропии:

(14)

Энтропия не убывает только в процессах изолированной системы, в неизолированной системе энтропия может и возрастать, и убывать, и оставаться неизменной. Рост энтропии в изолированной системе означает приближение системы к состоянию термодинамического равновесия; в этом состоянии S – максимальна, а dS=0.

Расчет изменения энтропии в различных процессах изучаемых систем зачастую является актуальной внутренней подзадачей разнообразных задач термодинамики, химии биологии, лингвистики. В частности, изменение энтропии служит мерой изменения качества энергии. Важнейшим условием для тепловых машин, работающих по произвольному циклу, является условие их максимально допустимой эффективности:

(за цикл) (15)

Большинство процессов, происходящих в природе, необратимы, например: диффузия, расширение, растворение. Для таких процессов вычисление энтропии основывается на том, что S – функция состояния. Если система перешла из одного состояния в другое необратимым образом, то можно мысленно заменить необратимый процесс обратимым, причем начальное и конечное состояния этого процесса должны быть равновесны, рассчитанное в этом случае изменение энтропии будет равно изменению энтропии при реальном необратимом процессе.

Задачи

3.1. Произвольное рабочее вещество совершает цикл, в пределах которого абсолютная температура изменяется в α раз. Цикл имеет вид изображенный на рис.15: T – температура, S – энтропия. Найти КПД цикла.

Рис.15

3.2. При очень низких температурах молярная теплоемкость кристаллов С^μ=aT³, где а – постоянная. Найти: а) удельную энтропию кристалла как функцию температуры в этой области; б) рассчитать удельную внутреннюю энергию кристалла при Т=100˚К.

3.3. Найти приращение энтропии алюминиевого бруска массы m=3.0кг при нагревании его от Т₁=300˚К до Т₂=600˚К, если в этом интервале температур удельная теплоемкость алюминия с=а+bТ, где а=0,77Дж/гК, b=0.46мДж/гК².

3.4. Вычислить изменения внутренней энергии и энтропии одного моля идеального газа при расширении по политропе pVⁿ=const от объема V₁ до объема V₂. рассмотреть частные случаи изотермического и адиабатического процессов.

3.5. Гелий массы m=1,7г адиабатически расширили в n=3 раза и затем изобарически сжали до первоначального объема. Найти приращение энтропии газа в этом процессе.

3.6. В двух сосудах одного и того же объема находятся различные идеальные газы. Масса газа в первом сосуде М₁, во втором М₂, давления газов и их температуры одинаковы. Сосуды соединили друг с другом и начался процесс диффузии. Определить суммарное изменение ∆S энтропии рассматриваемой системы, если относительная молекулярная масса первого газа μ₁, а второго μ₂.

3.7. Идеальный одноатомный газ в количестве υ=10 молей, находящийся при температуре Т₁=300˚К, расширяется без подвода и отдачи тепла в пустой сосуд через турбину, необратимым образом совершая работу (рис.16) После установления равновесия температура газа понижается до Т=200˚К.

Рис.16

После этого газ квазистатически сжимается: сначала изотермически, а затем адиабатически, возвращаясь в первоначальное состояние. При этом сжатии затрачивается работа А=15кДж. Найти изменение энтропии газа при расширении.

3.8. Вычислить изменение энтропии при смешении одноатомного идеального газа массы m₁, имеющего начальную температуру Т₁ и давление p₁, и двухатомного газа массы m₂, имеющего начальные температуру Т₂ и давление p₂. Молярные массы смешиваемых газов М₁ и М₂.

Ответы

3.1.

3.2.

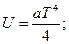
3.3.

3.4.

где k=const;

3.5.

3.6.

3.7.

3.8.

Семинар 4. Реальные газы

Уравнение состояния газа Клапейрона-Менделеева имеет ограниченную область применимости, поскольку не учитывает межмолекулярные взаимодействия. В реальных газах есть дальнодействующие силы притяжения и короткодействующие силы отталкивания. Взаимодействие в газах приводит к количественным и качественным отклонениям от поведения, предсказываемого уравнением Клапейрона-Менделеева.

Существует множество уравнений реальных газов, адекватно описывающих их свойства, включая превращение в жидкость. Это уравнения Ван-дер-Ваальса, Дитеричи (16), Бертло (17), Клаузиуса (18). Наиболее популярные в современной научной практике уравнения Редлиха-Квонга, Пенга-Робинсона, Камерлинг-Оннеса, или вириальное уравнение (19).

Рис.17

Уравнение Ван-дер-Ваальса имеет наиболее простую и физически ясную структуру, позволяющую сравнительно легко получать решение в аналитической форме. По этим причинам на семинаре мы ограничимся рассмотрением именно этого уравнения. Исторически это было первое уравнение состояния неидеального газа, поэтому наш выбор отражает также и почтение к его автору. Взаимодействие молекул на далеких и близких расстояниях удобно характеризовать потенциальной энергией взаимодействия

, функцией расстояния r между центрами молекул (рис.17).

Уравнения состояния реальных газов

- уравнение Дитеричи (16),

- уравнение Бертло (17),

- уравнение Клаузиуса (18),

- уравнение Камерлинг-Онесса (19).

Функция имеет минимум, в котором силы притяжения уравновешиваются силами отталкивания. Аналитический вид функции на полуэмпирической основе представлен ниже:

- потенциал Леннарда-Джонса (20)

В теории Ван-дер-Ваальса используется упрощенная модель межмолекулярного взаимодействия, часть кривой заменяется вертикальной прямой (пунктирная линия на рис.17). Если d – расстояние до этой прямой от начала координат, то центры взаимодействия частиц не могут сблизиться на расстояние, меньшее d, что соответствует модели твердых упругих шаров.

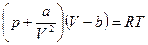- уравнение Ван-дер-Ваальса (21)

где 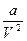– поправка на давление, т.е. дополнительное «внутреннее» давление за счет взаимного притяжения; b – поправка на объем молекул, учитывающая силы отталкивания.

Наиболее содержательные результаты получаются из уравнения Ван-дер-Ваальса путем анализа его изотерм. Если в уравнении (19) принять Т = const, то изотерма этого уравнения в плоскости p, V пересекается прямой линией p = const либо в одной точке, либо в трех точках (рис.18). При некоторой промежуточной температуре Т_кр три корня V_1, V₂, V₃ становятся равными.

Такая температура и соответствующая ей изотерма называются критическими. Критическая изотерма всюду монотонно опускается вниз, за исключением одной точки – критической.

Соответствующие этой точке давление p_k, объем V_k и температура T_k также называются критическими.

Рис.18

Существует два способа нахождения критических параметров: