Ряды с неотрицательными членами часто встречаются в различных приложениях. Сразу отметим основное свойство таких рядов: последовательность частичных сумм ряда с неотрицательными членами является неубывающей.
Теорема
Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.
Доказательство
По определению сходящегося ряда последовательность его частичных сумм сходится, значит, она необходимо ограничена. Что касается достаточности, то ограниченная монотонная неубывающая последовательность сходится в силу признака сходимости монотонной последовательности.
Определим несколько признаков, позволяющих устанавливать сходимость или расходимость числового ряда.
Теорема
Пусть для двух рядов с неотрицательными членами
| (9.3.1) |
| (9.3.2) |
выполняется неравенство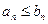 
для всех n. Тогда из сходимости ряда (9.3.2) следует сходимость ряда (9.3.1).
Рассмотрим несколько примеров применения Теоремы 2 по установлению сходимости (расходимости) неотрицательных рядов.
Пример
Исследовать сходимость ряда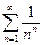 
.
Решение
Поскольку 
при 
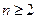, а ряд 
сходится (сумма бесконечно убывающей геометрической прогрессии), то сходится и данный ряд.
Пример
Исследовать сходимость ряда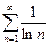 
.
Решение
Так как 
для достаточно больших n (это легко проверить по правилу Лопиталя для функции 
при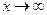 
, a> 0), то 
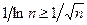. Ряд 
расходится, значит расходится и данный ряд.
Теорема
Пусть ряд (9.3.1) – ряд с неотрицательными членами, а ряд (9.3.2) – ряд с положительными членами. Если существует предел
| (9.3.3) |
то оба ряда сходятся или расходятся одновременно.
Теорема (признак Даламбера)
Пусть для ряда (9.3.1) с положительными членами существует предел
 .
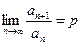| (9.3.4) |
Тогда этот ряд сходится при p< 1 и расходится при p> 1.
Замечание
При p= 1 необходимо дополнительное исследование ряда с других признаков, так как в этом случае ряд (9.3.1) может как сходится, так и расходится.
В качестве применения признака Даламбера исследуем сходимость следующих рядов.
Пример
Исследовать сходимость ряда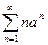 
, a> 0.
Решение
Составим соотношение 
и перейдем к пределу(9.3.4).
. По признаку Даламбера имеем: если a> 1. то данный ряд расходится, если же a< 1, то данный ряд сходится.
Пример
Исследовать сходимость ряда 
, a> 0.
Решение
Находим предел отношения
т.е. при a<e данный ряд сходится, при a>e он расходится.
Теорема (признак Коши)
Если существует предел
 ,
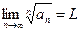| (9.3.5) |
то ряд (9.3.1 ) сходится при L< 1 и расходится при L> 1.
Пример
Исследовать сходимость ряда 
, где 
.
Решение
Применяя признак Коши, получаем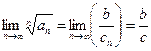 
. Следовательно, при b<c данный ряд сходится, а при b>c он расходится.
Теорема (интегральный признак сходимости)
Пусть функция f(x) непрерывная, положительная и убывающая всюду на промежутке 
. Тогда числовой ряд
| (9.3.6) |
сходится вместе с несобственным интегралом
 .
| (9.3.7) |
Пример
Исследовать сходимость ряда 
, a> 1.
Решение
Членами этого ряда являются значения функции 
в целочисленных точках. Ранее было исследовано, что соответствующий несобственный интеграл первого рода 
сходится при a> 1 и расходится при 
. Следовательно, данный ряд также сходится при a> 1 и расходится при . В частности, отсюда следует расходимость так называемого гармонического ряда:
.
