Определение
Дифференциальное уравнение вида
 ,
| (8.3.1) |
где 
и 
– непрерывные функции, называется уравнением с разделяющимися переменными.
Подчеркнем, что правая часть уравнения представляет собой произведение, в котором один сомножитель зависит только от x, а другой – только от 
. Метод решения такого вида уравнений носит название разделения переменных.
Запишем производную 
в ее эквивалентной форме, т.е. как отношение дифференциала функции к дифференциалу аргумента, затем умножим на 
обе части уравнения и поделим на 
обе части уравнения, полагая, что 
.
| (8.3.2) |
Интегрируя слева по переменной 
, а справа по переменной 
, получим
 ,
| (8.3.3) |
где 
– произвольная постоянная.
Рассмотрим примеры решения уравнений методом разделения переменных.
Пример
Найти частное решение уравнения 
по начальным условиям: 
при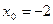 
.
Решение
Разделим переменные 
. Интегрируя обе части этого уравнения, имеем: 
, где – произвольная постоянная. При потенцировании получаем 
или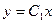 
. Полученная функция представляет собой семейство интегральных кривых. Для выделения частного решения используем начальные условия: 
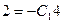, т.е. 
. Окончательно частное решение имеет вид: 
.
Пример
Найти решение уравнения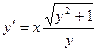 
, проходящее через точку 
.
Решение
Разделяя переменные, получаем уравнение в дифференциалах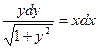 
.
Интегрируя, имеем 
. После интегрирования, получаем: 
.
Найдем константу. Для этого подставим в общее решение значения . Получим, что 
, т.е. эта кривая описывается уравнением (с учетом выбора знака): 
.
Определение
Дифференциальное уравнение первого порядка называется неполным, если 
явно зависит только от одной переменной: либо от 
, либо от .
Различают два случая такой зависимости.
1. Пусть функция зависит только от . Переписав это уравнение в виде 
нетрудно убедиться, что его решением является функция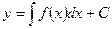 
.
2. Пусть функция зависит только от , тогда уравнение имеет вид 
. Дифференциальное уравнение такого вида называется автономным. Такие уравнения часто употребляются при математическом моделировании и исследованиях стационарных физических процессов, когда, независимая переменная играет роль времени. В этом случае особый интерес вызывают так называемые точки равновесия, или стационарные точки – нули функции 
, где производная 
.
Решение такого автономного уравнения методом разделения переменных приводит к функциональному уравнению вида 
.
Пример
Решить уравнение 
.
Решение
Полагая, что 
, решаем уравнение методом разделения переменных:
, где 
.
Заметим, что общее решение уравнения при 
дает частное решение 
, «потерянное» в процессе преобразований.
