Определение
Уравнения вида
 ,
| (8.4.1) |
называется однородным, если 
и 
однородные функции степени 
.
Понятие однородного дифференциального уравнения связано с понятием однородной функции.
Определение
Функция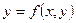 
называется однородной функцией степени , если для произвольного числа 
выполняется равенство 
.
Пример
Выяснить, являются ли однородными следующие функции:
а) 
. Так как 
, то данная функция однородна степени 2.
б) 
, 
. Функция однородна степени 0.
в)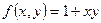 
, 
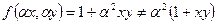. Данная функция неоднородная.
Дифференциальное уравнение вида (8.4.1) можно привести к виду
| (8.4.2) |
и при помощи подстановки 
(
– неизвестная функция) преобразовать в уравнение с разделяющимися переменными. Поскольку 
, то 
. После того, как общее решение последнего уравнения будет найдено, необходимо вернуться к старой функции 
.
Пример
Решить уравнение 
.
Решение
Разделим уравнение почленно на 
. Получим 
. Выполним замену 
. Следовательно, . Подстановка в исходное уравнение дает 
– уравнение с разделяющимися переменными. Решая его, получим 
. Возвращаясь к функции , получим общее решение уравнения: 
.
Логарифмирование решения дает: 
.
Пример
Найти частное решение уравнения 
в точке 
.
Решение
Уравнение однородное нулевой степени – 
или 
. В результате подстановки 
получим уравнение с разделяющимися переменными относительно функции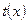 
: 
. Интегрирование этого уравнения дает функцию: 
. Следовательно, общее решение исходного уравнения имеет вид: 
. Частное решение, соответствующее начальному условию, имеет вид: 
.
Определение
Дифференциальное уравнение вида
 .
| (8.4.3) |
где 
и 
– непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Неизвестная функция и ее производная входят в указанное уравнение линейно, что и объясняет название уравнения.
Если 
, то уравнение (8.4.3) называется линейным однородным уравнением, если же 
, то уравнение (8.4.3) называется линейным неоднородным уравнением.
Пусть линейное однородное уравнение.
| (8.4.4) |
соответствует уравнению (8.4.3). Мы рассмотрим так называемый метод вариации постоянной – метод решения неоднородного уравнения, основанный на предварительном решении однородного уравнения (8.4.4).
Уравнение (8.4.2) можно решить методом разделения переменных:
, откуда 
.
Потенцируя, получаем общее решение уравнения (8.4.4):
 ,
| (8.4.5) |
где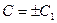 
.
Общее решение неоднородного уравнения (8.4.3) ищем в виде (8.4.5), полагая константу 
новой неизвестной функцией от аргумента .
 .
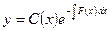| (8.4.5а) |
Подставим решение (8.4.5а¢) в уравнение (8.4.3).
,
откуда после приведения подобных получаем уравнение для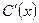 
:
 .
| (8.4.6) |
Интегрирование уравнения (8.4.4) дает выражение для 
: 
.
Подставляя выражение для в формулу общего решения, получаем окончательное выражение для решения неоднородного уравнения:
 ,
| (8.4.7) |
где 
– произвольная постоянная.
Следует отметить, что некоторые нелинейные уравнения приводятся к линейным уравнениям соответствующими заменами неизвестной функции . К таковым относится уравнение Бернулли:
 ,
| (8.4.8) |
где и – непрерывные функции, а 
– некоторое постоянное число. При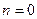 
имеем линейное неоднородное уравнение, а при 
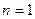– линейное однородное уравнение 
.
Пусть 
и 
. Введем новую функцию 
. Тогда 
. Поделим обе части уравнения (8.4.8) на 
и умножим на 
: 
.
Выполняя замену, получим линейное неоднородное уравнение относительно новой функции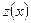 
: 
. Метод решения последнего нами уже изучен.
Пример
Решить уравнение 
.
Решение
Это линейное неоднородное уравнение первого порядка. Сначала решим соответствующее однородное уравнение 
. Разделяя переменные, получим 
.
Полагая функцией от и подставляя найденное решение в исходное неоднородное уравнение, получаем после приведения подобных дифференциальное уравнение для : 
.
После интегрирования этого уравнения и подстановки в уже найденное решение однородного уравнения получим искомое общее решение исходного уравнения: 
.
Пример
Решить уравнение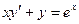 
.
Решение
Опять начнем с однородного уравнения 
. После разделения переменных и интегрирования уравнения получаем общее решение однородного уравнения 
. Полагая, что 
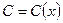, получаем после подстановки в неоднородное уравнение 
. Откуда 
. Стало быть, общее решение исходного уравнения имеет вид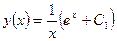 
.
Пример
Решить уравнение 
.
Решение
Данное нелинейное уравнение представляет собой уравнение Бернулли при 
. Заменой искомой функции 
мы получим линейное неоднородное уравнение относительно :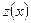 
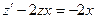. По формуле (8.4.7) получаем общее решение этого уравнения 
. Теперь выполняя обратную замену 
, получаем решение исходного нелинейного уравнения: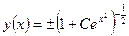 
Рассмотрим еще один из возможных способов решения линейного неоднородного уравнения (8.4.3) и уравнения Бернулли (8.4.8).
Решение этих уравнений ищем в виде произведения двух функций 
. Тогда линейное уравнение и уравнение Бернулли сводятся к двум уравнениям с разделяющимися переменными.
Так как 
, то линейное уравнение (8.4.3) преобразуется к виду 
.
Найдем сначала какое–нибудь частное решение уравнения 
. Тогда функция 
- решение уравнения 
.
Пример
Решить уравнение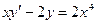 
.
Решение
Исходное уравнение есть линейное неоднородное уравнение 
. Пусть , тогда . Следовательно, 
или 
. Положим 
. Проинтегрировав это уравнение, найдем какое–нибудь частное решение этого уравнения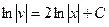 
. Например, при 
получаем 
. Подставляя в уравнение 
функцию , получим уравнение относительно функции 
: 
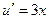. Решением этого уравнения с разделяющимися переменными есть функция 
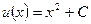. Окончательное выражение для решения исходного уравнения имеет вид 
.
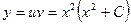