Определение
Совокупность уравнений вида
| (8.7.1) |
где 
–независимая переменная, 
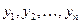– искомые функции, 
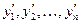– их производные, называется системой дифференциальных уравнений первого порядка.
Система дифференциальных уравнений, разрешенных относительно производных от неизвестных функций, называется нормальной системой дифференциальных уравнений и имеет следующий общий вид:
 .
| (8.7.2) |
Совокупность 
функций
| (8.7.3) |
определенных в интервале 
, называется решением нормальной системы (8.7.2), если эти функции при подстановке в уравнение системы (8.7.2) обращают их в тождество.
Теорема (Коши)
Пусть для системы дифференциальных уравнений первого порядка (8.7.2) выполняются следующие условия:
- функции 
, 
определены и непрерывны по всем аргументам в замкнутой области 
,
- частные производные 
непрерывны в области .
Тогда существует одна и только одна система решений уравнений (2):
 ,
| (8.7.4) |
определенная в некоторой окрестности точки 
и удовлетворяющая в этой точке заданным начальным условиям:
 .
| (8.7.5) |
Условия (8.7.5) называются начальными условиями решения, а задача отыскания решения по заданным начальным условиям – задачей Коши.
Совокупность n функций
| (8.7.6) |
зависящих от и произвольных постоянных 
, будем называть общим решением системы (8.7.2) в некоторой области , если при любых значениях постоянных эти функции представляют решение системы и если любое решение этой системы может быть записано в виде (8.7.6) при некоторых значениях постоянных .
Совокупность функций
| (8.7.7) |
получающееся из общего решения (6) системы (8.7.2) при определенных значениях постоянных 
будем называть частным решением системы (8.7.2).
Если в области выполнены условия теоремы Коши, то для нахождения частного решения (8.7.7) достаточно разрешить уравнения
| (8.7.8) |
относительно и подставить найденные значения постоянных в соотношения (8.7.6).
Одним из основных методов нахождения решения нормальных систем является метод исключения постоянных. С помощью этого метода данная система сводится к одному уравнению n–го порядка относительно одной неизвестной функции.
Пример
Найти общее решение системы уравнений 
и выделить из него частное решение, удовлетворяющее начальным условиям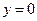 
, 
при 
.
Решение
Продифференцировав первое из уравнений системы по , получаем 
. Подставляя в это равенство выражение 
из второго уравнения системы и заменяя функцию 
ее выражением из первого, приходим к линейному однородному уравнению второго порядка относительно одной неизвестной функции: 
. Решив это уравнение, находим его общее решение 
. Дифференцируя последнее равенство, имеем 
. Подставляя выражения для 
и 
в первое уравнение системы и приводя подобные члены, получим 
.
Окончательно, общее решение системы имеет вид
, 
.
Решим теперь задачу Коши. Подставив в систему (*) вместо y, z и x их начальные значения 0, 1 и 0, получаем систему уравнений для определения постоянных 
и 
: 0= 
1+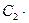 
0, 1=(
+ ) 
+( - ) 
.
Отсюда =0, =1. Следовательно, искомым частным решением являются функции 
, 
.
Если правые части нормальной системы (8.7.2) являются линейными функциями относительно неизвестных функций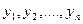 
, то такая система называется линейной и имеет вид
| (8.7.9) |
Если функции 
тождественно равны нулю, то линейная система называется однородной, в противном случае – неоднородной.
Системы линейных однородных диф. уравнений с постоянными коэффициентами
Рассмотрим систему трех уравнений с тремя неизвестными функциями x, e и z:
| (8.7.10) |
где 
– вещественные числа, t – независимая переменная.
Будем искать частное решение системы (8.7.10) в следующем виде:
| (8.7.11) |
где a, b, g и k некоторые числа (причем 
), которые надо определить так, чтобы функции (8.7.11) были решением системы (8.7.10).
Подставляя функции (8.7.11) и их производные в уравнения системы (8.7.10) и сокращая на 
, получим
Перенося все члены в одну часть равенства и группируя коэффициенты при a, b, g получим систему уравнений
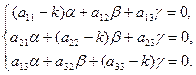
| (8.7.12) |
Система (8.7.12) – это однородная система трех уравнений первой степени с тремя неизвестными a, b и g. Как известно, чтобы эта система имела ненулевое решение, необходимо и достаточно, чтобы определитель был равен нулю, т.е. число k было корнем уравнения
| (8.7.13) |
Уравнение (8.7.13) называют характеристическим уравнением для системы (8.7.10). Оно является уравнением третьей степени относительно k и имеет три корня: 
. Каждому корню соответствует ненулевое решение системы (8.7.12) (
), а следовательно, и частное решение данной системы (8.7.10):
Если корни 
характеристического уравнения различны и вещественны, то общее решение системы (8.7.10) запишется в виде
 или 
| (8.7.14) |
где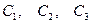 
– произвольные постоянные.
В случае, когда среди корней характеристического уравнения имеются кратные, корню 
кратности r соответствует частное решение системы (8.7.10), имеющее вид
| (8.7.15) |
где 
– многочлены степени не выше 
.
Пример
Найти общее решение системы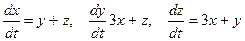 
.
Решение
Ищем частное решение системы в виде 
. Подставляя эти функции в систему, получаем
| (П.1) |
Составляем характеристическое уравнение 
. Отсюда получаем уравнение 
. Корни характеристического уравнения 
различны и вещественны.
Найдем частное решение, соответствующее корню 
. Подставим его значение в систему (П.1). Полагая 
, находим 
. Решение имеет вид 
.
Аналогично для корня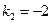 
получаем 
. Решение имеет вид 
.
Третий корень 
дает 
. Решение 
.
Общее решение системы имеет вид
Пример
Найти общее решение системы 
Решение
Ищем частное решение в виде 
. При этом получаем характеристическое уравнение: 
или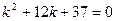 
. Корни этого уравнения 
комплексно сопряженные. Для первого корня имеем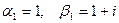 
и, значит, 
– решение данной системы.
Аналогично для второго корня частное решение равно 
. Выделив из обоих частных решений вещественные части, получаем общее решение системы
Пример
Найти общее решение системы
| (П.2) |
Решение
Характеристическое уравнение 
, или 
имеет корни 
Найдем частное решение вида 
соответствующее корню 
. Из системы имеем 
. Искомым частным решением являются функции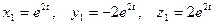 
.
Теперь найдем два частных решения, соответствующих кратному корню 
.
Согласно (8.7.15), ему отвечает решение вида
| (П.3) |
Коэффициенты 
определяются подстановкой (П.3) в систему (П.2). Выбрав в качестве произвольных коэффициенты 
, найдем 
. Решения (П.3) принимают вид 
.
Полагая сначала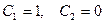 
, а затем 
, находим два частных решения, соответствующих кратному корню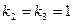 
: 
И, наконец, общим решением данной системы являются функции
.
Упражнения
Проинтегрировать следующие уравнения различных типов:
| 1. | 
| 2. | 
|
| 3. | 
| 4. |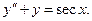 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
Проинтегрировать следующие системы.уравнений:
| 11. | 
| 12. | 
|
| 13. | 
| 14. | 
|
Глава 9. Ряды
Основные понятия. Сходимость ряда
Определение: Рассмотрим числовую последовательность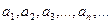 
. Образуем из элементов этой последовательности выражение вида
 ,
| (9.1.1) |
которое называется числовым рядом, или просто рядом. Слагаемые в формуле (9.1.1) называются членами ряда. Суммы первых n членов ряда называются частичными суммами ряда:
 ,  , …, 
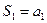| (9.1.2) |
Поскольку число членов ряда бесконечно, то частичные суммы ряда образуют числовую последовательность 
:
 .
| (9.1.3) |
Ряд (9.1.1) называется сходящимся, если существует предел S последовательности частичных сумм (9.1.3); в таком случае число S называется суммой ряда:
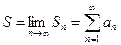
| (9.1.4) |
Если же последовательность частичных сумм (9.1.3) не имеет предела, числовой ряд (9.1.1) называется расходящимся.
Рассмотрим примеры числовых рядов.
1. Дан ряд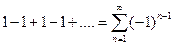 
. Последовательность частичных сумм этого ряда 
не имеет предела, т.е. ряд расходится.
2. Дан ряд составленный из элементов геометрической прогрессии с первым членом 
и знаменателем 
: 
.
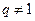Частичная сумма этого ряда выражается формулой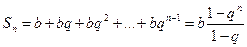 
.
1. При | q |< 1 пределом является число 
, которое также будет и суммой данного ряда.
2. При | q |> 1 предел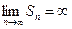 
и ряд расходится.
3. Если же | q |= 1, то данный ряд также расходится.
