C помощью определенного интеграла можно решать различные задачи в области физики, техники, геометрии, также в области экономики. Например, с помощью определенного интеграла вычисляются длины траекторий, движения, площади различных фигур, объемы тел и пр.
Вычисление площадей плоских фигур
Пусть функция  неотрицательна и непрерывна на отрезке
неотрицательна и непрерывна на отрезке 
 . Тогда по геометрическому смыслу определенного интеграла площадь S под кривой
. Тогда по геометрическому смыслу определенного интеграла площадь S под кривой  на
на  численно равна определенному интегралу
численно равна определенному интегралу  , т.е.
, т.е.  .
.
Пример
Найти площадь фигуры, ограниченной линиями  ,
,  ,
,  .
.
Решение
Из Рис. 7.14.1 видно, что площадь криволинейного треугольника ОАВ равна разности двух площадей:  . Решая систему
. Решая систему  , получаем координаты точки В (точки пересечения кривой
, получаем координаты точки В (точки пересечения кривой 
 и прямой
и прямой  В
В  . Тогда
. Тогда 
 .
.
Окончательно  .
.
Отметим, что данная задача может быть решена другим способом.
По определению определенного интеграла  .
.
Это равенство можно понимать так, что при построении интегральной суммы разбиению подвергается отрезок  оси ординат. Соответственно точки
оси ординат. Соответственно точки  – это ординаты, фиксированные на каждом из отрезков разбиения. Поэтому, если
– это ординаты, фиксированные на каждом из отрезков разбиения. Поэтому, если  на
на  , то интеграл
, то интеграл  численно равен площади криволинейной трапеции, ограниченной кривой
численно равен площади криволинейной трапеции, ограниченной кривой  и прямыми
и прямыми  ,
,  ,
,  .
.

Рис. 7.14.1
Возвращаясь к нашей задаче, можно посчитать площадь следующим образом:
 .
.
Если функция  не положительна и непрерывна на отрезке
не положительна и непрерывна на отрезке  , то площадь
, то площадь  над кривой
над кривой  на
на  отличается знаком от определенного интеграла
отличается знаком от определенного интеграла  :
:
 .
.
Пример
Найти площадь фигуры, ограниченной линиями  ,
,  ,
,  .
.
Решение
Из Рис. 7.14.2 видно, что искомая площадь  криволинейного треугольника ОАВ может рассматриваться как площадь над кривой ОАВ на отрезке
криволинейного треугольника ОАВ может рассматриваться как площадь над кривой ОАВ на отрезке  . Однако указанная кривая (ломаная)не задается одним уравнением. Поэтому для нахождения площади необходимо разбить треугольник ОАВ на две части
. Однако указанная кривая (ломаная)не задается одним уравнением. Поэтому для нахождения площади необходимо разбить треугольник ОАВ на две части  . Координаты точек есть
. Координаты точек есть  ,
,  и
и  .
.

 ,
,  .
.
Окончательно,  .
.

Рис. 7.14.2
Несобственные интегралы
При рассмотрении определенного интеграла как предела интегральных сумм предполагалось, что подынтегральная функция ограничена на конечном отрезке интегрирования. Данное Определение определенного интеграла не имеет смысла, если не выполняется хотя бы одно из этих условий. Нельзя разбить бесконечный интеграл на конечное число отрезков конечной длины. Если подынтегральная функция неограниченна, то интегральная функция не имеет предела. Тем не менее возможно обобщить понятие предела и на эти случаи, с чем и связано понятие несобственного интеграла.
Интегралы с бесконечными пределами интегрирования
Определение
Пусть функция  определена на промежутке
определена на промежутке  и интегрируема на любом отрезке
и интегрируема на любом отрезке  ,
,  , так что интеграл
, так что интеграл

имеет смысл. Предел этого интеграла при 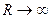 называется несобственным интегралом первого рода и обозначается
называется несобственным интегралом первого рода и обозначается
  . .
| (7.15.1) |
В том случае, если этот предел конечен, говорят, что несобственный интеграл сходится, а функцию  называют интегрируемой на бесконечном промежутке
называют интегрируемой на бесконечном промежутке  ; если же предел в формуле (7.15.1) бесконечен или не существует, то говорят, что несобственный интеграл расходится.
; если же предел в формуле (7.15.1) бесконечен или не существует, то говорят, что несобственный интеграл расходится.
Аналогичным образом вводится понятие несобственного интеграла по промежутку  :
:
  . .
| (7.15.2) |
Наконец, несобственный интеграл с двумя бесконечными пределами можно определить как сумму несобственных интегралов (7.15.1) и (7.15.2):
 , ,
| (7.15.3) |
где с – любое число.
Геометрический смысл несобственного интеграла первого рода основан на геометрической интерпретации определенного интеграла на отрезке  : это площадь бесконечной области, ограниченной сверху неотрицательной функцией
: это площадь бесконечной области, ограниченной сверху неотрицательной функцией  , снизу – осью Ох, слева – прямой
, снизу – осью Ох, слева – прямой  (см. Рис.1). Такая же интерпретация имеет место и для несобственных интегралов (7.15.2) и (7.15.3).
(см. Рис.1). Такая же интерпретация имеет место и для несобственных интегралов (7.15.2) и (7.15.3).
Рассмотрим несколько примеров несобственных интегралов первого рода.
Пример
 ,
,
но предела функции  при
при 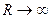 не существует, т.е. данный интеграл расходится.
не существует, т.е. данный интеграл расходится.
Пример
 ,
,

Рис. 7.15.1
т.е. данный интеграл сходится.
Пример
 .
.
Конечный предел существует – значит исходный интеграл сходится.
Пример



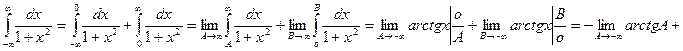
 .
.
Интегралы от неограниченных функций
Рассмотрим функцию  , определенную на промежутке
, определенную на промежутке  , но неограниченную на нем. Для определенности положим, что
, но неограниченную на нем. Для определенности положим, что  ограничена и интегрируема на любом отрезке
ограничена и интегрируема на любом отрезке  ,
,  , но не ограничена в любой окрестности точки
, но не ограничена в любой окрестности точки 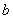 или на промежутке
или на промежутке  . В таком случае точка
. В таком случае точка  называется особой точкой.
называется особой точкой.
Определение
Предел интеграла  при
при  называется несобственным интегралом второго рода и обозначается
называется несобственным интегралом второго рода и обозначается
 . .
| (7.15.4) |
Если этот предел конечный, то говорят, что интеграл (7.15.4) существует или сходится, а функцию  называют интегрируемой на промежутке
называют интегрируемой на промежутке  ; если же предела нет или он бесконечен, то говорят, что интеграл (7.15.4) расходится.
; если же предела нет или он бесконечен, то говорят, что интеграл (7.15.4) расходится.
Аналогично, если особой точкой является точка  , то несобственный интеграл второго рода определяется как
, то несобственный интеграл второго рода определяется как
 . .
| (7.15.5) |
Если функция  неограниченна в окрестности некоторой внутренней точки
неограниченна в окрестности некоторой внутренней точки  , то определению полагают, что
, то определению полагают, что
 . .
| (7.15.6) |
Наконец, если  и
и  – особые точки, т.е. функция
– особые точки, т.е. функция  ограничена и интегрируема на интервале
ограничена и интегрируема на интервале  , то несобственный интеграл второго рода определяется в виде суммы
, то несобственный интеграл второго рода определяется в виде суммы
 ,
,
где с – произвольная точка на  , а несобственные интегралы второго рода в правой части этого равенства определяются по формулам (23.1.4) и (23.1.5).
, а несобственные интегралы второго рода в правой части этого равенства определяются по формулам (23.1.4) и (23.1.5).
Рассмотрим несколько примеров на вычисление несобственных интегралов второго рода.
Пример
 ,
,
т.е. данный интеграл сходится.
Пример
Найти интеграл, учитывая, что особыми являются точки 1 и–1.

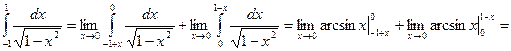

Следовательно, данный несобственный интеграл второго рода сходится.
Пример
 .
.
Предел равен  , поэтому интеграл расходится.
, поэтому интеграл расходится.
Признаки сходимости несобственных интегралов
Теорема (признак сравнения несобственных интегралов)
Пусть функции  и
и  непрерывны на промежутке
непрерывны на промежутке  и удовлетворяют на нем условию
и удовлетворяют на нем условию  . Тогда из сходимости интеграла
. Тогда из сходимости интеграла  следует сходимость интеграла
следует сходимость интеграла  и наоборот, из расходимости интеграла
и наоборот, из расходимости интеграла  следует расходимость интеграла
следует расходимость интеграла  .
.
Замечание
Аналогичный признак сравнения справедлив и для несобственных интегралов второго рода.
Рассмотрим примеры использования признака сравнения несобственных интегралов.
Пример
 .
.
Сравним подынтегральную функцию в этом интеграле с функцией  . Очевидно, что
. Очевидно, что  . Интеграл
. Интеграл  сходится, следовательно, в силу признака сравнения сходится и данный интеграл.
сходится, следовательно, в силу признака сравнения сходится и данный интеграл.
Пример
 .
.
Сравним подынтегральную функцию в этом интеграле с функцией  . Очевидно, что
. Очевидно, что  . Поскольку интеграл
. Поскольку интеграл  сходится, то сходится и исходный интеграл.
сходится, то сходится и исходный интеграл.
Теорема (признак Абеля–Дирихле)
Пусть функция  непрерывна и имеет ограниченную первообразную
непрерывна и имеет ограниченную первообразную  на промежутке
на промежутке  , а функция
, а функция  имеет непрерывную производную на этом промежутке, не возрастает и стремится к нулю при
имеет непрерывную производную на этом промежутке, не возрастает и стремится к нулю при  . Тогда несобственный интеграл
. Тогда несобственный интеграл

| (7.15.7) |
сходится.
Рассмотрим примеры использования признака Абеля – Дирихле сходимости несобственных интегралов.
Пример
 .
.
Если принять в качестве  , а в качестве
, а в качестве  , то легко убедиться, что все требования, накладываемые на функции, выполнены, т.е. данный интеграл сходится.
, то легко убедиться, что все требования, накладываемые на функции, выполнены, т.е. данный интеграл сходится.
Упражнения
Вычислить интегралы:
| 1. | 
| 2. | 
|
| 3. | 
| 4. | 
|
Интегрирование методом подстановки:
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
| 11. | 
| 12. | 
|
Интегралы вида 
| 13. | 
| 14. | 
|
| 15. | 
| 16. | 
|
Интегралы вида 
| 17. | 
| 18. | 
|
| 19. | 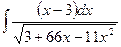
| 20. | 
|
Интегрирование по частям:
| 21. | 
| 22. | 
|
| 23. | 
| 24. | 
|
Применить тригонометрические подстановки в следующих примерах:
| 25. | 
| 26. | 
|
| 27. | 
| 28. | 
|
Интегрирование рациональных дробей:
| 29. | 
| 30. | 
|
| 31. | 
| 32. | 
|
Интегрирование иррациональных функций:
| 33. | 
| 34. |

|
| 35. | 
| 36. | 
|
Интегралы вида 
| 37. | 
| 38. | 
|
| 39. | 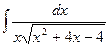
| 40. | 
|
Интегрирование тригонометрических функций:
| 41. | 
| 42. | 
|
| 43. | 
| 44. | 
|
Пользуясь формулой Ньютона—Лейбница, вычислить определенные интегралы:
| 45. | 
| 46. | 
|
| 47. | 
| 48. | 
|
Вычислить значения нижеследующих интегралов, применяя указанные подстановки:
| 49. | 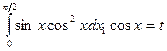
| 50. | 
|
Вычислить следующие несобственные интегралы:
| 51. | 
| 52. | 
|
| 53. | 
| 54. | 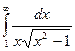
|




