С абсолютными величинами чисел в математическим анализе приходиться часто встречаться Мы Напомним относящееся сюда определения и теоремы и сделаем ряд упражнений.
1. Абсолютная величина 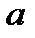 обозначается символом
обозначается символом 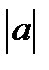 .
.
Пусть  —действительное число. Если оно положительно или равно нулю
—действительное число. Если оно положительно или равно нулю  , то его абсолютной величиной называется оно само, а если оно отрицательно
, то его абсолютной величиной называется оно само, а если оно отрицательно  , то его абсолютной величиной называется число
, то его абсолютной величиной называется число  .
.
Итак, если  , то
, то 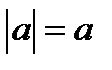 ; если
; если 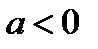 , то
, то  .
.
Чтобы перейти к абсолютной величине числа, имеющего в цифровой записи знак минус, надо этот знак отбросить.
Если 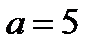 , то
, то  ; если
; если 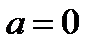 , то
, то  .
.
Если  , то
, то  .
.
2. Если  , то это означает, что
, то это означает, что  удовлетворяет неравенствам (фиг.1.5);
удовлетворяет неравенствам (фиг.1.5);
| Фиг.1.5 |
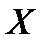
|

|

|

|

|
Пример1. Если  , то имеют место неравенства
, то имеют место неравенства 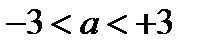 .
.
Пример 2. Если  , то
, то  удовлетворяет неравенствам
удовлетворяет неравенствам  (фиг.1.6)
(фиг.1.6)

|

|
| Фиг.1.6 |

|
|
Задача1.1
Определить числовую величину выражения  при
при  .
.
Решение. При 

Задача1.2
Определить числовую величину выражения  при
при  .
.
Решение. При  имеем
имеем

Задача1.3
(для самостоятельного решения).Определить при  числовую величину выражения
числовую величину выражения  .
.
Ответ. 
Задача1.4
(для самостоятельного решения).Найти числовую величину выражения  при:
при:
1)  ;
;
2)  ;
;
3)  .
.
Ответ
1) 5;
2) 3;
3) 8.
Задача1.5
Определить, при каких значениях 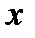 будет справедливо неравенство
будет справедливо неравенство  .
.
Решение. Согласно формуле (1.1) данное неравенство может быть записано так:  . К каждой части этих неравенств прибавим по 3 и получим
. К каждой части этих неравенств прибавим по 3 и получим  , откуда следует, что
, откуда следует, что  .
.
Заключение: неравенство  выполняется для всех значений
выполняется для всех значений 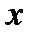 из интервала (1,5).
из интервала (1,5).
Задача1.6
Определить, при каких значениях  выполняется неравенство
выполняется неравенство 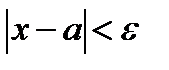 .
.
Решение. Поступая так де, как и предыдущей задаче, получаем, что  , а отсюда, прибавляя
, а отсюда, прибавляя  к каждой части этих неравенств, имеем
к каждой части этих неравенств, имеем  .
.
Заключение: неравенство  выполняется для всех значений
выполняется для всех значений  из интервала
из интервала 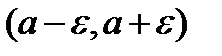 .
.
Задача1.7
(для самостоятельного решения).Определить, при каких  выполняется неравенства:
выполняется неравенства:
1)  ;
;
2)  ;
;
3)  .
.
Ответ.
1)  ;
;
2)  ;
;
3)  и
и  .
.
Указание к третьему примеру: из того, что 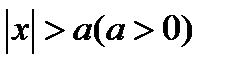 , следует, что
, следует, что 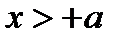 и
и 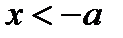 . В нашем случае из того, что
. В нашем случае из того, что  , заключаем, что
, заключаем, что  и
и 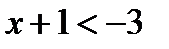 ; отсюда и следует указанный ответ.
; отсюда и следует указанный ответ.
Задача1.8
При каких значениях  корень
корень  будет иметь действительное значения?
будет иметь действительное значения?
Решение. Корень  будет иметь действительное значение, если подкоренное выражение не является отрицательным, т. е. когда
будет иметь действительное значение, если подкоренное выражение не является отрицательным, т. е. когда  , а
, а  .
.
Многие совершают грубую ошибку, делая на основании неравенства  заключение, что
заключение, что  , т.е.
, т.е.  и
и 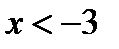 . В действительности же верно только то, что
. В действительности же верно только то, что  , а неравенство
, а неравенство 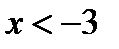 является в данном случае ошибочным. Правильным решением неравенства
является в данном случае ошибочным. Правильным решением неравенства  являются
являются  и
и  , т.е.
, т.е.  , или
, или  , ибо для всех значений
, ибо для всех значений  из интервала
из интервала 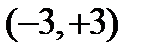 выполняется неравенство
выполняется неравенство  . Если же принять, что
. Если же принять, что  , то числа, удовлетворяющие этому неравенству, будучи возведены в квадрат, дадут числа больше, чем 9 (например,
, то числа, удовлетворяющие этому неравенству, будучи возведены в квадрат, дадут числа больше, чем 9 (например,  и
и 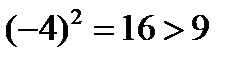 ).
).
Итак, решением неравенства 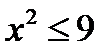 является
является  , или
, или 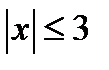 .
.
Задача1.9
(для самостоятельного решения). При каких значениях 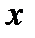 корень
корень  будет иметь действительное значение?
будет иметь действительное значение?
Ответ.  и
и 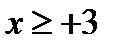 , т.е.
, т.е. 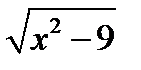 имеет действительные значения для значений
имеет действительные значения для значений 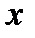 , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  и
и  .
.






