Линейный оператор, действия над ними. Собственные векторы и собственные значения линейных операторов, их свойства и нахождение.
Литература: [1] –C.202-221; [2] – C.78-86.
Тема 6. Квадратичные формы.
Квадратичные формы. Закон инерции квадратичных форм. Положительно и отрицательно определённые квадратичные формы. Критерии знакоопределённости квадратичных форм.
Литература: [1] –C.251-261; [2] – C.86-91.
Раздел II. ВЕКТОРНАЯ АЛГЕБРА
Тема 7. Векторная алгебра.
Геометрические векторы на прямой, плоскости и в пространстве, действия над ними. Проекция вектора. Прямоугольная декартова система координат. Радиус-вектор. Координаты вектора. Линейные операции над векторами в координатной форме. Длина и направляющие косинусы вектора. Расстояние между точками. Деление отрезка в данном отношении. Скалярное, векторное, смешанное произведения векторов, их свойства, выражение в координатной форме, приложения для решения геометрических задач. Условия перпендикулярности, параллельности и компланарности векторов.
Литература: [1] –C.5-37; [2] – C.63-68; [3] – C.301-305; [4] – C.222-241.
Раздел III. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Тема 8. Прямые линии и плоскости.
Прямая на плоскости и в пространстве. Различные виды уравнений прямой на плоскости ив пространстве. Расстояние от точки до прямой на плоскости. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Плоскость. Различные виды уравнений плоскости. Расстояние от точки до плоскости. Взаимное расположение прямой и плоскости.
Литература: [1] –C.45-71; [2] – C.95-104; 119-121;
[3] – C.91-94; 305-311; [4] – C.34-52; 244-252.
Тема 9. Кривые и поверхности второго порядка.
Кривые 2-ого порядка на плоскости: окружность, эллипс, гипербола, парабола, их определения, канонические уравнения, форма. Приведение общего уравнения кривой 2-ого порядка к каноническому виду и построение. Поверхности 2-ого порядка, их канонические уравнения и форма.
Литература: [1] –C.72-110; [2] – C.104-115; [3] – C.95-98; 311-318;
[4] – C.52-69; 252-259.
Тема 10. Системы линейных неравенств. Линейные задачи оптимизации.
Системы линейных неравенств. Решение линейных неравенств в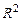 
. Постановка задачи линейного программирования, графический метод её решения.
Литература: [5] – C.271-293.
Рекомендуемая литература.
Основная литература:
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М: Наука, 1998.
2. Кремер Н.Ш., Путко Б.А., Тришин И.М., Фридман М.Н. Высшая математика для экономистов. Учеб. пособие для вузов. -М.: ЮНИТИ-ДАНА, 1997.
3. Красс М.С. Математика для экономических специальностей. Учебник. –М.: ИНФРА-М, 1998.
4. Шипачев В.С. Высшая математика. Учебник для вузов. -М. Высшая школа, 2002.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х частях. Часть 1. Учеб. пособие для втузов. -М: Высшая школа, 1997.
6. Сборник задач по математике для втузов. Часть1. Линейная алгебра и основы математического анализа. Под ред. Ефимова А.В., Демидовича Б.П. -М: Наука, 1993.
Дополнительная литература:
7. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике: Учебник: В 2-х частях. Ч.1. –М.: Финансы и статистика, 2000.
8. Общий курс высшей математики для экономистов. Учебник / Под ред. В.И.Ермакова. М: ИНФРА-М, 1999.
9. Зимина О.В., Кириллов А.И., Сальникова Т.А. Решебник. Высшая математика. М.: Физматлит, 2001.
10. Практикум по высшей математике для экономистов: Учеб.пособие для вузов/ Кремер Н.Ш., Тришин И.М., Путко Б.А. и др. Под ред.проф.Н.Ш.Кремера. –М.:ЮНИТИ-ДАНА, 2002.
11. Сборник задач по математике для вузов. Под ред. Котляра Л.М., Углова А.Н. -Наб. Челны: Изд-во КамПИ, 2004, 2006, 2007.
