В общем случае кривая второго порядка в базисе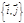 
описывается уравнением 
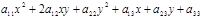. Ее первые три слагаемые образуют квадратичную форму 
с матрицей:
.
Задача о приведении кривой 
к каноническому виду сводится к задаче о приведении к каноническому виду квадратичной формы 
этой кривой.
Пусть 
и 
– собственные значения матрицы 
, а 
и 
– ортонормированные собственные векторы матрицы 
, соответствующие собственным значениям 
и 
.
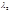Ортонормированные векторы 
и 
называются главными направлениями этой кривой.
Пусть 
является матрицей перехода от ортонормированного базиса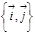 
к ортонормированному базису 
.
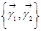Тогда ортогональное преобразование:
приводит квадратичную форму к каноническому виду 
, а уравнение кривой – к виду 
в прямоугольной декартовой системе координат 
, оси которой направлены вдоль векторов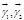 
, а начало совпадает с точкой 
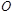системы координат 
.
Выделив в этом уравнении полные квадраты, получим 
, где 
– некоторые числа. Осуществив параллельный перенос системы координат 
в новое начало 
, получим канонический вид уравнения 
в системе координат 
. В зависимости от чисел 
эта кривая будет эллипсом, гиперболой, параболой, парой прямых, точкой или мнимой кривой.
31ВОПРОС Комплексные числа и действия над ними. Сопряжённые числа. Алгебраическая, тригонометрическая и показательная формы комплексных чисел. Формулы Муавра и Эйлера.
Пара а,b действительных чисел а и b называются упорядоченной, если указано какое из них первое, какое второе. Комплексное число –это упорядоченная пара.
равны, если а=с и b=d. сумма: 
, умножение: 
отсюда
Сложение: чтобы сложить два компл. числа надо отдельно сложить их действительные и мнимые части. z=x+iy (x,y- действительные переменные i-мнимая единица). (a+bi)+(c+di)=(a+c)+(b+d)i;
Вычитание: необходимо вычесть отдельно их действительные и мнимые части.
(a+bi)-(c+di)=(a-c)+(b-d)i;
Произведение: (a+bi) (c+di)=(aс-bd)+(bc+ad)i;
Деление: a+bi/c+di = ac+bd/c2 +d2+bc-ad/c2+d2 
i
Возведение в степень - формула бинома Ньютона 
Если дано 
, то число а-bi, отличающееся от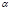 
только знаком при мнимой части называют сопряжённым числу 
и обозначают 
.
Сумма и произведение двух комплексно-сопряжённых чисел 
- действительные числа: 
Упорядоченную пару i=(0,1), где i2=-1 называют мнимой единицей, с её помощью можно выразить упоряд. пару: bi=(b,0)(0,1)=(0,b)то(a,b)=(a,0)+(0,b)= =a+bi т.е. (a,b)=a+bi – алгебраическая форма.
, поскольку а=r cos 
то 
r 
- триганометрическая форма
Формула Эйлера: ввёл в обозначение I для мнимой единицы (i= 
)
Формула Муавра: если n –натуральное число и z=r(cos 
+I sin ),то zn=r(cos +I sin ))n = rn(cosn +isin n ).
32ВОПРОС Алгебраические многочлены. Теорема Безу. Основная теорема алгебры. Разложение многочлена на множители над полем комплексных и над полем действительных чисел. Разложение рациональных функций на простейшие дроби. Методы вычисления коэффициентов разложения.
Многочлен - это алгебраическая сумма одночленов. Степень многочлена есть наибольшая из степеней одночленов, входящих в данный многочлен.
Основная теорема алгебры:
всякий многочлен n -й степени с комплексными коэффициентами в множестве комплексных чисел имеет ровно n корней, если каждый кратный корень считать такое число раз, какова его кратность.
Основная теорема алгебры справедлива и при n =0, так как многочлен нулевой степени корней не имеет. Основная теорема алгебры неприменима лишь к нулевому многочлену (числу нуль), степень которого не определена.