Выражение скалярного произведения через координаты

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

т.е

 

9 ВОПРОС Скалярное произведение векторов. Условие перпендикулярности двух векторов. Механический смысл скалярного произведения векторов.

Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается ab,а* b(или(а, b)).Итак, по определению,

Формуле (6.1) можно придать иной вид. Так как | a| cosg=пр _ba, (см. рис.14), a |b| cosg = пр _ab, то получаем:

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

условие перпендикулярности ненулевых векторов а и b:

Механический смысл скалярного произведения векторов. Скалярное произведение силы F на вектор перемещения S равно работе А этой силы при перемещении материальной точки по вектору S: A = FS.

 

 

10 ВОПРОС Ориентация тройки векторов в пространстве. Векторное произведение векторов. Физический смысл векторного произведения векторов. Условие коллинеарности векторов. все упорядоченные некомпланарные тройки векторовмогут быть разбиты на два непересекающихся класса: правые тройки и левые тройки. Определение 1:: Упорядоченная тройка некомпланарных векторов а1, а2, а3 называется правой, если наблюдателю, находящемуся внутри телесного угла, образованного этими векторами, кратчайшие повороты от а1 ка2 и от а2 к а3 кажутся происходящими против часовой стрелки. Если повороты происходят по часовой стрелке, то тройка – левая.

Есть и ещё один способ разделить эти два класса: Правило правой руки:Совместите начала всех векторов тройки в одной точке. Представьте, что в этой точке находится ладонь Вашей правой руки. Совместите большой палец с первым вектором базиса, а указательный – со вторым. Если теперь вы сможете совместить средний палец с третьим вектором, то рассматриваемая тройка векторов – правая. Если нет – левая. Выбрав один из двух классов и назвав все входящие в него базисы “положительными” мы зададим ориентацию пространства. Далее будем считать положительными правые тройки векторов. Все дальнейшие определения будем давать с учетом этого Векторное произведение векторов Определение 3:: Векторным произведением упорядоченной пары векторов a и b называется вектор [a,b], такой что 1. | [a,b] |=Sa,b, где Sa,b – площадь параллелограмма, построенного на векторах a и b. (Если a || b, то Sa,b=0.) 2. a [a,b] b. a, b, [a,b] – правая тройка. Свойства векторного произведения: 1. [a,b] = -[b,a] 2.[a,b] = θ  a || b 3.[a1+a2,b] = [a1,b]+[a2,b] 4.λ·[a,b] = [λ·a,b] = [a,λ·b] λ R. Выясним физический смысл векторного произведения. Если вектор изображает приложенную в некоторой точке М с илу, а вектор идет из некоторой точки О в точку М, то вектор = [ ] представляет собой момент силы относительно точки О. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными. Условия коллинеарности векторов -Два вектора коллинеарные, если отношения их координат равны. -Два вектора коллинеарные, если их векторное произведение равно нулю.

 

 

11вопрос Смешанное произведение векторов. Условие компланарности трех векторов.

Смешанное произведение векторов и его свойства.
Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a * b * c =[ a * b ]* c = a *[ b * c ], где a ={ax,ay,az} b ={bx,by,bz} c ={cx,cy,cz}
Св-ва:
1. При перестановке 2х сомножителей:
a * b * c =- b * c * a
2. не меняется при перестановке циклических сомножителей:
a * b * c = c * a * b = b * c * a
3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a * b * c =0
б)если некомпланарные вектора a, b, c привести к 1 началу, то | a * b * c |=Vпараллепипеда, построенного на этих векторах
если a * b * c >0, то тройка a, b, c - правая
если a * b * c <0, то тройка a, b, c – левая

Компланарность векторов. Условия компланарности векторов.

Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.

Условия компланарности векторов

Три вектора компланарны если их смешанное произведение равно нулю.

Три вектора компланарны если они линейно зависимы.

 

12 вопрос

Общее уравнение прямой: Ах + Ву + С = 0,где А и В не равны нулю одновременно.

Коэффициенты А и В являются координатами нормального вектора прямой (т.е. вектора, перпендикулярного прямой). При А = 0 прямая параллельна оси ОХ, при В = 0 прямая параллельна оси ОY.

При В 0 получаем уравнение прямой с угловым коэффициентом:

Уравнение прямой, проходящей через точку (х ₀ , у ₀) и не параллельной оси OY, имеет вид: у – у ₀ = m (x – х ₀),где m – угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ. При А 0, В 0 и С 0 получаем уравнение прямой в отрезках на осях:

где a = – C / A, b = – C / B. Эта прямая проходит через точки (a, 0) и (0, b), т.е. отсекает на осях координат отрезки длиной a и b.

Уравнение прямой, проходящей через две различные точки (х ₁, у ₁) и (х ₂, у 2):

Параметрическое уравнение прямой, проходящей через точку (х ₀ , у ₀) и параллельной направляющему вектору прямой (a, b):

Условие параллельности прямых:

1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0: AE – BD = 0

2) для прямых у = m x+ k и у = p x+ q: m = p.

Условие перпендикулярности прямых:

1) для прямых Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0: AD + BE = 0

2) для прямых у = m x+ k и у = p x+ q: m p = – 1

Расстояние между двумя точками (x ₁, y ₁) и(x ₂, y ₂)

Расстояние от точки (х ₀ , у ₀) до прямой Ах+ Ву+ С = 0

Расстояние между параллельными прямыми Ах+ Ву+ С = 0 и Dх+ Eу+ F = 0

Угол между прямыми:

13Эллипс. Его характеристики.

 

Эллипсом (рис.1) называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F ₁ и F ₂ , называемых фокусами эллипса, есть величина постоянная

Уравнение эллипса (рис.1):

Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ (рис.1), при a < b фокусы эллипса лежат на оси ОY, а при a = b эллипс становится окружностью (фокусы эллипса в этом случае совпадают с центром окружности). Таким образом, окружность есть частный случай эллипса.

Отрезок F ₁ F ₂ = 2 с, где , называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осьюэллипса. Число e = c / a, e < 1 называется эксцентриситетом эллипса.

Пусть Р (х ₁, у ₁) – точка эллипса, тогда уравнение касательной к эллипсу в данной точке имеет вид:

Условие касания прямой y = m x + k и эллипса х ² / a ² + у ² / b ² = 1:

k ² = m ² a ²+ b ².

 

14.Гипербола. Ее характеристики.

Гиперболой (рис.1) называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек F ₁ и F ₂ , называемых фокусами гиперболы, есть величина постоянная.

Уравнение гиперболы (рис.1):

Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии.

Отрезок F ₁ F ₂ = 2 с, где 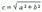, называется фокусным расстоянием. Отрезок AB = 2 a называется действительной осью гиперболы, а отрезок CD = 2 b – мнимой осьюгиперболы. Число e = c / a, e > 1 называется эксцентриситетомгиперболы. Прямые y = ± (b / a) x называются асимптотами гиперболы.

Пусть Р (х ₁, у ₁) – точка гиперболы, тогда уравнение касательной к гиперболе в данной точке имеет вид:

Условие касания прямой y = m x + k и гиперболы х ² / a ² – у ² / b ² = 1:

k ² = m ² a ²– b ².

Свойства:

-Гипербола не имеет общих точек с осью Oy, а ось Ox пересекает в двух точках A (a; 0) и B (– a; 0), которые называются вершинами гиперболы.

- Гипербола имеет две взаимно перпендикулярные оси симметрии.

- Гипербола имеет центр симметрии.

- Гипербола пересекается с прямой y = kx при в двух точках.

 

 

15Парабола. Ее характеристики.

Параболой (рис.1) называется геометрическое место точек, равноудалённых от заданной точки F, называемой фокусом параболы, и данной прямой, не проходящей через эту точку и называемой директрисой параболы.

Уравнение параболы (рис.1): y ² = 2 p x.

Здесь ось ОХ является осью симметрии параболы.

Пусть Р (х ₁, у ₁) – точка параболы, тогда уравнение касательной к параболе в данной точке имеет вид: у ₁ y = p (x + х ₁).

Условие касания прямой y = m x + k и параболы y ² = 2 p x:2 m k = p.

Свойства параболы:

1Парабола — кривая второго порядка.

2Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.

3Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.

4Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.

5Парабола является антиподерой прямой.

6Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.

 

 

16 Общее уравнение кривых второго порядка в декартовой системе координат. Параллельный перенос осей координат. Поворот осей координат.

Общее уравнение кривых второго порядка в декартовой системе координат имеет вид

Ах²+2Вху+Су²+2Dx+2Ey+F=0

Параллельный перенос. Передвинем систему координат X Y Z в трёхмерном пространстве так, чтобы оси OX, OY и OZ оставались параллельны самим себе, а начало координат О сместилось в точку О' (a, b, с). Получим новую систему координат X' Y' Z'.

Координаты точки Р в новой и старой системе координат связаны соотношениями:

Поворот осей координат.

Пусть даны две декартовы системы координат с одинаковым началом О и разными направлениями осей (рис. 70).

Пусть α есть угол между осями Ох и ОХ. Обозначим через х, у и X, Y координаты произвольной точки М соответственно в старой и новой системах:

х = | ОР |, у = | РM |,

X = | ОР₁ |, Y = | Р₁M |.

Рассмотрим ломаную линию ОР₁MP и возьмем ее проекцию на ось Ох. Замечая, что проекция ломаной линии равна проекции замыкающего отрезка имеем: ОР₁MP = | ОР |. (4)

С другой стороны, проекция ломаной линии равна сумме проекций ее звеньев следовательно, равенство (4) запишется так: пр ОР₁ + пр Р₁M + пp MP =| ОР

Так как проекция направленного отрезка равна его величине, умноженной на косинус угла между осью проекций и осью, на которой лежит отрезок (гл. I, § 8), то пр ОР₁ = X cos α пр Р₁M = Y cos (90° + α) = — Y sin α, пp MP = 0.

Отсюда равенство (4') нам дает: x = X cos α — Y sin α. (5)

Аналогично, проектируя ту же ломаную на ось Оу, получим выражение для у. В самом деле, имеем: пр ОР₁ + пр Р₁M + пp MP = пp ОР = 0.

y = X sin α + Y cos α. (6)

Из формул (5) и (6) мы получим новые координаты X и Y выраженными через старые х и у, если разрешим уравнения (5) и (6) относительно X и Y.

 

 

17ВопросУравнение кривых второго порядка в полярной системе координат.

Общее уравнение второго порядка

+ 2 ху + + х + у + = 0

1 Уравнение окружности в центре (; ) R

(х - )² + (у - )² = R² х² + у² = R²

2 Эллипс – геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. + = 1

3 Гипербола – кривая второго порядка, которая в некоторой системе координат описывается уравнением + = 1

где а > 0, b > 0 – параметры гиперболы.

Точка пересечения гиперболы с осью ОХ (± а, 0) называется вершинами гиперболы. С осью ОY гипербола не пересекается.

Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b)

+ = -1

4Парабола – кривая второго порядка, которая в некоторой системе координат описывается уравнением = 2 рх где р > 0 – параметры параболы.

 

18 вопрос

Общее уравнение плоскости Ах + Ву + Сz + D = 0,где А, B и C не равны нулю одновременно.Коэффициенты А, B и C являются координатами нормального вектора плоскости (т.е. вектора, перпендикулярного плоскости).

При А 0, В 0, С 0 и D 0 получаем уравнение плоскости в отрезках на осях:

где a = – D / A, b = – D / B, c = – D / C. Эта плоскость проходит через точки (a, 0, 0), (0, b, 0) и (0, 0, с), т.е. отсекает на осях координат отрезки длиной a, b и c.

Уравнение плоскости, проходящей через точку (х ₀ , у ₀, z ₀ ) и перпендикулярной вектору (А, В, C): А (х – х ₀) + В (у – у ₀) + С (z – z ₀) = 0.

Условие параллельности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:

AF – BE = BG – CF = AG – CE = 0.

Условие перпендикулярности плоскостей Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:

АE+ ВF+ СG = 0.

Расстояние между двумя точками (х ₁ , у ₁, z ₁ ) и(x ₂, y ₂, z ₂):

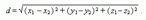
Расстояние от точки (х ₀ , у ₀, z ₀ ) до плоскости Ах + Ву + Сz + D = 0:

Угол между плоскостями Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0:

 

19 ВОПРОС Прямая в пространстве. Способы ее задания. Взаимное расположение двух прямых в пространстве. Угол между двумя прямыми.

Уравнение прямой, проходящей через две различные точки (х ₁, у ₁, z ₁) и (х ₂, у ₂ , z ₂):

Параметрическое уравнение прямой, проходящей через точку (х ₀ , у ₀, z ₀) и параллельной направляющему вектору прямой (a, b, с):

Пусть заданы две плоскости Ах+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0, причём их нормальные векторы неколлинеарны, тогда система уравнений

 

 

описывает прямую – линию пересечения этих плоскостей.

Пусть (a, b, с) и (p, q, r) – направляющие векторы двух прямых, тогда имеем условие параллельности прямых: aq – bp = br – cq = ar – cp = 0,

условие перпендикулярности прямых: ap + bq + cr = 0,

угол между прямыми:

угол между прямой и плоскостью: