Евкли́дово простра́нство (также Эвкли́дово простра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность 3.
В современном понимании, в более общем смысле, может обозначать один из сходных и тесно связанных объектов, определённых ниже. Обычно 
-мерное евклидово пространство обозначается 
, хотя часто используется не вполне приемлемое обозначение 
.
1. Конечномерное гильбертово пространство, то есть конечномерное вещественное векторное пространство 
с введённым на нём (положительно определенным) скалярным произведением, порождающим норму: 
,в простейшем случае (евклидова норма):
где 
(в евклидовом пространстве всегда можно выбрать базис, в котором верен именно этот простейший вариант).
2. Метрическое пространство, соответствующее пространству описанному выше. То есть 
с метрикой, введённой по формуле:
,где 
и 
.
Неравенство Коши́ — Буняко́вского связывает норму и скалярное произведение векторов в евклидовом пространстве. Это неравенство эквивалентно неравенству треугольника для нормы.
Формулировка:Пусть дано линейное пространство 
со скалярным произведением 
. Пусть 
— норма, порождённая скалярным произведением, то есть 
. Тогда для любых 
имеем:
причём равенство достигается тогда и только тогда, когда векторы 
и 
пропорциональны (коллинеарны).
Ортогональный базис — базис, составленный из попарно ортогональных векторов.
Ортонормированный базис удовлетворяет еще и условию единичности нормы всех его элементов. То есть это ортогональный базис с нормированными элементами.
Последнее удобно записывается при помощи символа Кронекера: 
то есть скалярное произведение каждой пары базисных векторов равно нулю, когда они не совпадают (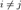
), и равно единице при совпадающем индексе, то есть когда берется скалярное произведение любого базисного вектора с самим собой.
Очень многое записывается в ортогональном базисе гораздо проще, чем в произвольном, поэтому очень часто стараются использовать именно такие базисы, если только это возможно или использование какого-то специального неортогонального базиса не дает особых специальных удобств. Или если не отказываются от него в пользу базиса общего вида из соображений общности.
Ортонормированный базис является самодуальным (дуальный ему базис совпадает с ним самим). Поэтому в нём можно не делать различия между верхними и нижними индексами, и пользоваться, скажем, только нижними (как обычно и принято, если конечно при этом используются только ортонормированные базисы).
Линейная независимость следует из ортогональности, то есть достигается для ортогональной системы векторов автоматически.
Коэффициенты в разложении вектора по ортогональному базису:
можно найти так:
.
Полнота ортонормированной системы векторов эквивалентна равенству Парсеваля: для любого вектора 
квадрат нормы вектора равен сумме квадратов коэффициентов его разложения по базису:
ВОПРОС 27 Линейные операторы. Матрица линейного оператора. Действия над линейными операторами. Зависимость между матрицами линейного оператора в различных базисах.
пусть заданы линейные пространства X и Y. Правило, по которому каждому элементу x e X ставится в соответствие единственный элемент y e Y, называется оператором, действующим в линейных пространствах X, Y. Результат действия оператора A на элемент x обозначают y = A x или y = A(x). Если элементы x и y связаны соотношением y = A x, то y называют образом элемента x; элемент x прообразом элемента y.
Множество элементов линейного пространства X, для которых определено действие оператора A, называют областью определения оператора и обозначают D(A).
Множество элементов линейного пространства Y, которые являются образами элементов из области определения оператора A, называют образом оператора и обозначают Im(A). Если y = A x, то x e D(A), y e Im(A).
Оператор A, действующий в линейных пространствах X, Y называется линейным оператором, если
A(u+v)=A(u)+A(v) и A(au)=aA(u) и для любых u,v e X и для любого числа a.
Если пространства X и Y совпадают, то говорят, что оператор действует в пространстве X. В дальнейшем ограничимся рассмотрением линейных операторов, действующих в линейном пространстве X.
