Цель работы
Научиться находить углы и расстояния в пространстве, используя понятия и свойства перпендикулярных прямых и плоскостей.
Ход работы
Вариант
2.1.1 Через точки А и В проведены прямые, перпендикулярные плоскости α, пересекающие её в точках А1 и В1 соответственно. Найдите _________________
____
____
____
если отрезок АВ не пересекает плоскость α.
2.1.2 Из точки А проведена к плоскости α наклонная АС. Найти синус угла наклона касательной к плоскости α, если ________________________________________
____
____
____
2.1.3 Прямые АВ, АС, АД попарно перпендикулярны. Найдите __________________
____
____
____
2.1.4 Через вершину квадрата АВСД проведена прямая ВО, перпендикулярная его плоскости. Найдите___________________________________________________
____
____
____
____
____
____
2.1.5 Из точки А к плоскости проведены две наклонные АВ и АС. Найдите ________
____
____
____
____
____
____
2.1.6 Две плоскости пересекаются под углом α. Найти cosα, если ________________
____
____
____
2.1.7 Точка Д равноудалена от вершин равностороннего треугольника АВС. Найти
____
____
____
____
____
____
2.1.8 Точка Д равноудалена от сторон равностороннего треугольника АВС. Найдите
____
____
____
____
____
____
Допуск к работе
2.2.1 
Запишите теорему Пифагора для треугольника АВС
2.2.2 Запишите формулу для вычисления синуса и косинуса угла АСВ
sin ACB = 
cos ACB =
2.2.3 Запишите формулы для вычисления радиуса вписанной и описанной
окружности правильного треугольника
_______
_______
_______
2.2.4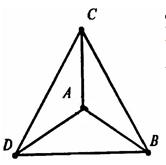 
Прямые АВ, АС, АД попарно перпендикулярны, выпишите все прямоугольные треугольники, изображённые на рисунке
|
2.2.5 Через вершину квадрата АВСД проведена прямая ВО, перпендикулярная его
плоскости. Выпишите все прямоугольные треугольники, изображённые на
рисунке и укажите, какой угол у них прямой.
____________________________
____________________________
____________________________
____________________________
2.2.6 Сформулируйте свойство точки равноудалённой от вершин многоугольника
_______
_______
_______
_______
2.2.7 Сформулируйте свойство точки равноудалённой от сторон многоугольника
_______
_______
_______
_______
2.2.8 Проведите из точки А перпендикуляр и две наклонные к плоскости
2.2.9 Постройте угол между плоскостями
К работе допускается ______________
Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 21
Координаты и вектора в пространстве.
Цель работы
Научиться выполнять действия над векторами, заданными своими координатами
Ход работы
Вариант
2.1.1 Построить параллелепипед АВСДА1В1С1Д1, пользуясь правилом треугольника или правилом параллелограмма, найти вектор, равный сумме векторов __________________________________
2.1.2 Даны вектора:
________________________________________________________________
Найти: а) скалярное произведение векторов 
и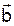 
б) координаты вектора _____________________________________
в) скалярный квадрат вектора _______________________________
г) проекцию вектора ____ на вектор _____
д) модуль вектора ______
е) найти координаты точки М, если N(_________) и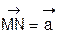 
2.1.3 При каком значении m вектора _____________________________________
будут перпендикулярны?
2.1.4 При каком значении k и n вектора __________________________________
будут коллинеарными?
2.1.5 Треугольник АВС задан координатами своих вершин
________________________________________________________________
Найти: а) периметр треугольника АВС
б) косинус угла между сторонами ____________________________
в) длину медианы _____
г) длину средней линии ____ || ____
д) координаты точки пересечения медиан
е) считая, что точки А, В, С – три вершины параллелограмма,
найти координаты четвёртой вершины.
Допуск к работе
2.2.1 Пусть известны координаты точек А(ха; уа; za) и В(хb; уb; zb). Запишите формулы для вычисления:
А) Координат вектора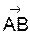 
_______________________________________
Б) Расстояния АВ ______________________________________________
В) Координат точки С - середины отрезка АВ ______________________________
2.2.2 Пусть известны координаты векторов 
(ах; ау; аz) и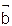 
(bx; by; bz). Запишите формулы для вычисления:
A) Координат вектора 
___________________________________
Б) Координат вектора 
___________________________________
В) Скалярного произведения векторов и ________________________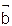
Г) Скалярного квадрата вектора _________________________________
Д) Проекции вектора на вектор ________________________________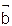
Е) Модуля вектора ___________________________________________
2.2.3 Запишите условие равенства векторов и 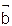, заданных своими координатами._________________________________
2.2.4 Запишите условие параллельности векторов и 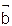, заданных своими координатами._________________________________
2.2.5 Запишите условие перпендикулярности векторов и 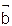, заданных своими координатами. __________________________________
_______________________________________________________
К работе допускается ______________
Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 22
