Цель работы
Научиться вычислять производную функции, используя таблицу производных и правила
дифференцирования
Ход работы
Вариант
Найдите производную функции с помощью формулы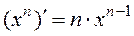 
:
1) 
Найдите производную функции, преобразовав по свойству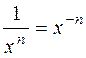 
:
2) 
Найдите производную функции, преобразовав по формуле 
:
3) 
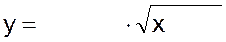
| 4) 
|
Найдите производную функции, применив правило 
:
5) 
| 6) 
|
Найдите производные сложных функций 
:
7) 
| 8) 
|
9) 
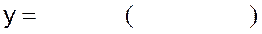
| 10) 
|
11) 
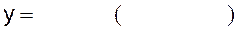
| 12) 
|
13) 
|
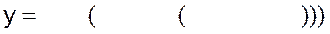
Найдите производные, применив правило 
:
14) 
| 15) 
|
16) 
|
17)Вычислите значение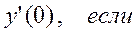  
|
Найдите производные, применив правило 
:
18) 
| 19) 
|
20)Вычислите значение 
|
2.2. Допуск к работе
2.2.1 Заполните таблицу производных:
| 
|
2.2.2 Допишите равенства:
| 
|
| 
|
| 
|
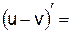
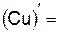
К работе допускается ______________
Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 14
Построение графиков функции с помощью производной.
Цель работы
Научиться исследовать функцию с помощью производной и строить по результатам исследования график
Ход работы
Вариант
Исследовать функцию и построить её график:
2.1.1
2.1.2
2.1.3
2.1.4
2.2. Допуск к работе
2.2.1 Заполните пропуски
А) Если производная дифференцируемой функции положительна на промежутке, то функция на этом промежутке _____________________.
Б) Если производная дифференцированной функции _________________ на промежутке, то функция на этом промежутке убывает.
В) Если для дважды дифференцируемой функции вторая её производная отрицательна внутри промежутка, то график функции является ______________ на данном промежутке.
Г) Если же вторая производная __________________ внутри промежутка, то график функции является вогнутым на данном промежутке.
2.2.2 Заполните пропуски
Схема исследования функции
1. Найдите область определения функции.
2. Определите четность, нечетность функции. (f(-x) = f(x) - ____________________
f(-x) = __________ - нечётная)
3 Найти точки пересечения графика функции с осями координат. (с осью ОХ у = ___, с осью _____ х = 0).
4. Найдите производную функции.
5. Определите стационарные и критические точки производной. Т. е. точки в которых производная равна ________ и не существует.
6. Определите промежутки монотонности (возрастания, _____________) и экстремумы (максимумы и ________________) функции.
7. Найдите значения функции в _________________________ и критических точках.
- Найдите вторую производную и исследуйте функцию на выпуклость и ____________.
 |
9. Для построения графика найдите необходимые дополнительные точки.
2.2.3 Дорисуйте схемы
А) Б)
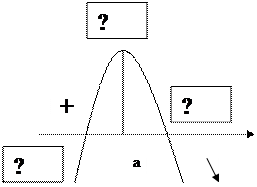
К работе допускается ______________
- Результаты работы
3.1
y =
1) Область определения функции D(f) =
2) Четность, нечетность функции
f(-x) =
_____________________
3) Точки пересечения графика функции с осями координат
А) с осью ОХ (у=0)
Б) с осью ОУ (х=0)
4) Первая производная: y’ =
5) Стационарные точки: (y’ = 0)
____________________
6) Промежутки монотонности (возрастания, убывания)
Возрастает _______________________
Убывает __________________________
7) Экстремумы:
Максимум: xmax = ymax =
Минимум: xmin = ymin =
8) Вторая производная у ‘’ =
 | |||
 |
Выпукла ____________________
Вогнута _____________________
9) График функции:
| х | |||||
| у |
3.2
y =
1) Область определения функции D(f) =
2) Четность, нечетность функции
f(-x) =
_____________________
3) Точки пересечения графика функции с осями координат
А) с осью ОХ (у=0)
Б) с осью ОУ (х=0)
4) Первая производная: y’ =
5) Стационарные точки: (y’ = 0)
____________________
6) Промежутки монотонности (возрастания, убывания)
Возрастает _______________________
Убывает __________________________
7) Экстремумы:
Максимум: xmax = ymax =
Минимум: xmin = ymin =
8) Вторая производная у ‘’ =
| |||
|
Выпукла ____________________
Вогнута _____________________
9) График функции:
| х | |||||
| у |
ПРАКТИЧЕСКАЯ РАБОТА 15
