Цель работы
1. 1 Научиться применять производную для решения геометрических и физических задач
1.2 Научиться применять производную для приближённых вычислений
Ход работы
Вариант
2.1.1 Вычислить приближённо е
2.1.2. Найдите тангенс угла наклона к оси ОХ касательной графика функции
2.1.3 Написать уравнение касательной к графику функции f(x)=
в точке с абсциссой х0 =
2.1.4 Материальная точка движется прямолинейно по закону
x(t) =
а) Записать формулы для вычисления скорости и ускорения движения
б) Найти скорость и ускорение в момент времени t =
в) Через сколько секунд после начала движения точка остановиться?
2.1.5 Найдите наибольшее и наименьшее значение функции f(x)=
на отрезке [; ]
2.1.6 Решите задачу:
________________________________________________________________
2.2. Допуск к работе
2.2.1. В чём заключается физический смысл производной
________________________________
2.2.2. Каков геометрический смысл производной?
________________________________
 |
2.2.3. Запишите уравнение касательной к графику функции
________________
2.2.4. Запишите алгоритм нахождения наибольшего и наименьшего значения функции на отрезке
________
________
________
________________________
________________
2.2.5. Запишите формулу для вычисления приближённого значения функции
________________
________
К работе допускается ______________
Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 16
Вычисление неопределённых интегралов
Цель работы
Научиться вычислять неопределённые интегралы
Ход работы
Вариант
Вычислить интегралы:
| 2.1.1. | 2.1.13 |
| 2.1.2 | 2.1.14 |
| 2.1.3 | 2.1.15 |
| 2.1.4 | 2.1.16 |
| 2.1.5 | 2.1.17 |
| 2.1.6. | 2.1.18 |
| 2.1.7 | 2.1.19 |
| 2.1.8 | 2.1.20 |
| 2.1.9 | 2.1.21 |
| 2.1.10 | 2.1.22 |
| 2.1.11 | 2.1.23 |
| 2.1.12 | 2.1.24 |
2.1.25 Скорость прямолинейного движения материальной точки задаётся формулой
v(t) =
Найдите закон движения S(t), если в момент времени t = с координата точки
равнялась.
2.1.26 Для функции у(х) = найдите первообразную, график которой проходит через точку М(;)
2.2. Допуск к работе
2.2.1 Заполните таблицу интегралов
1) 
2) 
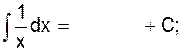
3) 
4) 
5) 
6) 
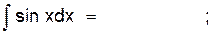
7) 
8) 
9) 
10) 
К работе допускается ______________
Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 17
Вычисление определённых интегралов.
Цель работы
Научиться вычислять определённые интегралы
Ход работы
Вариант
Вычислить интегралы:
| 2.1.1. | |
| 2.1.2 | |
| 2.1.3 | |
| 2.1.4 | |
| 2.1.5 | |
| 2.1.6. | |
| 2.1.7 | |
| 2.1.8 | |
| 2.1.9. | |
| 2.1.10. |
Допуск к работе
2.2.1 Выпишите формулу Ньютона - Лейбница
__________________________
2.2.2 Вычислите
| функция | х =0 | х = 
| х = 
| х = 
|
| y = cos5x | cos(5· )=cos  = -1
| |||
| y = sin5x |
| функция | х =1 | х = 
|
х = 
| х =
|
| y = lg x |
| функция | х =1 | х = e | х = e - 3 | х = e14 |
| y = ln x |
К работе допускается ______________
Результаты работы
ПРАКТИЧЕСКАЯ РАБОТА 18
Вычисление площадей плоских фигур с помощью
определённого интеграла.
Цель работы
Научиться вычислять площади плоских фигур с помощью определённого интеграла
Ход работы
Вариант
Вычислить площадь фигуры, ограниченной линиями:
| 2.1.1. |
| 2.1.2 |
| 2.1.3 |
| 2.1.4 |
| 2.1.5 |
Допуск к работе
2.2.1 Выпишите формулу для вычисления площади, заштрихованной фигуры
__________________________
|
____________________________
2.2.2 Начертите график функции
у = 2 х
| 
|
y= log 2 x
| 
|
y = sinx
| y = 2sinx
|
К работе допускается ______________
Результаты работы
<
Дата добавления: 2016-10-22; Мы поможем в написании ваших работ!; просмотров: 429 | Нарушение авторских прав Поиск на сайте: Лучшие изречения:  | 2263 -  |
Ген: 0.014 с.