Теорема о проекциях прямого угла

Помимо позиционных задач, рассмотренных в предыдущих параграфах, в практике приходится решать задачи на определение расстояний, углов и истинных величин плоских фигур. Такие задачи называются метрическими задачами. При их решении необходимо знать условие перпендикулярности прямых и плоскостей. Для этого надо выяснить свойство ортогональной проекции прямого угла.

Если одна сторона прямого угла параллельна плоскости проекций, то на эту плоскость проекций прямой угол проецируется без искажения (рис. 50).

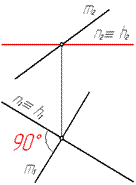
Рис. 50

На рис. 51 показаны скрещивающиеся прямые, перпендикулярные друг другу.

Рис. 51

Перпендикулярность прямой и плоскости

Из геометрии известно, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (рис. 52).

 

Рис. 52

Если прямые а и в будут прямыми общего положения, то прямой угол к ним ни на одной плоскости проекций не спроецируется в натуральную величину. Согласно теореме о проецировании прямого угла, прямой угол спроецируется в натуральную величину на плоскость проекций, если одна сторона прямого угла будет параллельной этой плоскости проекций. Поэтому, в качестве прямых надо взять горизонталь h и фронталь f. Тогда прямой угол между перпендикуляром n и h спроецируется в натуральную величину на П₁, а прямой угол между n и f – на П₂. На рис. 53 в точке К, принадлежащей плоскости α(а‖b), построен перпендикуляр n к плоскости.

Рис. 53

 

Применение дополнительного ортогонального проецирования

Для решения задач

Пример1. Найти длину отрезка АВ.

Чтобы найти длину отрезка занимающего в пространстве общее положение относительно плоскостей П₁ и П_2, надо построить дополнительную ортогональную проекцию отрезка АВ на плоскость П₄ ему параллельную (П₄‖АВ) и П₄^П₁ (рис. 54).

Рис.54

Поэтапное решение задачи на эпюре показано на рис. 55

Рис. 55

Пример 2. Построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П_4, перпендикулярной к плоскости α и к плоскости П_1.

Из геометрии известно, что две плоскости взаимноперпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости. В данном примере перпендикуляром к плоскости П₄ является горизонталь h (рис. 56).

 

Рис. 56

Исходя из этого, ось х₁₄ проведена перпендикулярно горизонтальной проекции h₁ горизонтали h плоскости ΔАВС (рис. 57).По отношению к плоскости П₄ плоскость ΔАВС является проецирующей и изображается на ней в виде прямой А₄В₄С_4.

 

Рис. 57

Пример 3. Построить дополнительную ортогональную проекцию прямой общего на плоскость ей перпендикулярную.

Для этого надо сначала построить дополнительную ортогональную проекцию прямой АВ на плоскость ей параллельную (П₄‖АВ) и П₄^П₁.Ось х₁₄ построена параллельно А₁В₁. Затем построить дополнительную ортогональную проекцию прямой АВ на плоскость П₅ ей перпендикулярную(П₅^ АВ) и П₅^ П₄ (рис. 58). Ось х₄₅ построена перпендикулярно А₄В₄. На плоскости П₅ прямая будет точкой.

Рис. 58

Рещение задачи на эпюре показано на рис. 59

Рис. 59

 

Пример 4. Определить размеры треугольника АВС.

Чтобы найти величину ΔАВС,являющегося плоскостью общего положения,надо построить его дополнительную ортогональную проекцию на плоскость ему параллельную. Для этого надо сначала построить дополнительную ортогональную проекцию плоскости общего положения α(ΔАВС) на плоскости П_4,перпендикулярной к плоскости α(ΔАВС) и к плоскости П₁ (см.пример 2). А затем построить его дополнительную ортогональную проекцию на плоскость П₅ ему параллельную (П₅‖ ΔАВС) и П₅^ П₄ (рис.60). Решение задачи на эпюре показано на рис.61.

Рис.60

Рис.61

Пример 5. Определить расстояние между двумя параллельными прямыми m и n (рис.62).

Перпендикуляр, опущенный из любой точки одной прямой на другую, определяет расстояние между прямыми.

Обе параллельные прямые m и n параллельны плоскости П₁. Зададим точку А на прямой m и опустим из этой точки А перпендикуляр на прямую n по теореме о проекциях прямого угла А₁В₁^n_1..Отрезок АВ является отрезком общего положения. Найдем его натуральную величину. Для этого спроецируем его на плоскость ему параллельную-П₄‖АВ и П₄^П₁. Новая ось Х₁₄ проведена через горизонтальную проекцию А₁В₁.На линиях связи от новой оси Х₁₄ откладываем отрезки, равные расстояниям от А₂ и В₂ до оси х₁₂.Расстояние между А₄ и В ₄ и будет искомым.

Рис.62

Пример 6. Определить расстояние между скрещивающимися прямыми l и m, l ^П₁ и m – прямая общего положения (рис.63).

Под расстоянием между скрещивающимися прямыми понимается длина отрезка перпендикуляра, общего для обеих прямых.

Если одна из скрещивающихся прямых l перпендикулярна к плоскости проекций П₁, то их общий перпендикуляр АВ параллелен плоскости проекций П₁. При этом прямой угол между перпендикуляром и прямой m проецируется на плоскости П₁ в прямой угол, и проекция отрезка перпендикуляра А₁В₁ между прямыми l и m определяет расстояние между ними.

Рис.63

Пример 7. Определить расстояние между скрещивающимися прямыми l и m ( обе общегоположения) (рис.64).

Расстояние между скрещивающимися прямыми представляет собой длину отрезка, перпендикулярного обеим прямым.. В данной задаче обе прямые l и m занимают общее положение, значит необходимо одну из прямых, пусть это будет прямая l, преобразовать в проецирующую. Таким образом, решение задачи сводится к следующему:

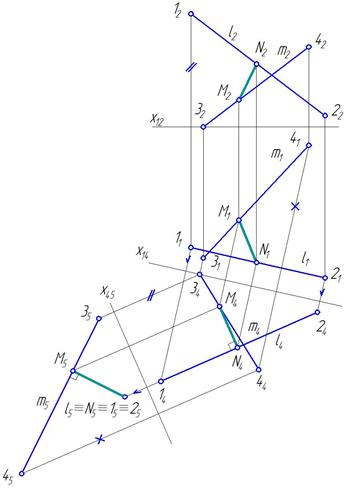
Рис.64

1. Построить дополнительную ортогональную проекцию прямой l (на ней заданы точки 1 и 2) и прямой m (на ней заданы точки 3 и 4) на плоскости П₄, параллельной прямой l и перпендикулярной к П₁ (П₄ ‖ l и П₄ ^ П₁).При этом ось x₁₄ параллельна l₁ (x₁₄ ‖ l₁).

2. Построить дополнительную ортогональную проекцию прямой l и прямой m на плоскости П₅, перпендикулярной к прямой l и перпендикулярной к П₄ (П₅ ^ l и П₅ ^ П₄; x₄₅ ^ l₄).

3. На плоскости П₅ определить искомое расстояние между скрещивающимися прямыми l и m, опустив перпендикуляр из точки l₅ на проекцию m₅ ([ M₅N₅ ] ^ m₅ , / MN / =/ M₅N₅ /).

4. Построить остальные проекции отрезка [ MN ], при этом [ M₄N₄ ] ^ l₄ согласно теореме о проекциях прямого угла.

Пример 8. Определить расстояние от точки А до плоскости α(h∩f) (рис.65).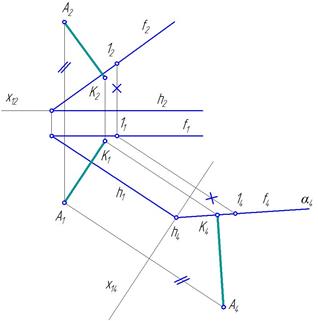

Рис.65

Расстояние от точки до плоскости измеряется длиной отрезка перпендикуляра, опущенного из точки на плоскость. Если плоскость является проецирующей, то этот отрезок будет параллелен той плоскости проекций, которой перпендикулярна заданная плоскость, и проецироваться на эту плоскость проекций в натуральную величину. Преобразуем плоскость α(h∩f) из общего положения в проецирующее. Для этого необходимо построить дополнительную ортогональную проекцию плоскости α (h∩f) на плоскость ей перпендикулярную, чтобы заданная плоскость α стала проецирующей α₄. При этом дополнительная плоскость проекций П₄ должна быть одновременно перпендикулярна и к плоскости α, и к одной из двух исходных плоскостей проекций, например, плоскости П₁, т.е. П₄ ^ α и П₄ ^ П₁. На эпюре это условие соблюдается в том, что ось x₁₄ проведена перпендикулярно к горизонтальной проекции h₁ горизонтали h плоскости α, что следует из того, что плоскость П₄ будет перпендикулярна к плоскости α, если она перпендикулярна к горизонтали этой плоскости. Дополнительной ортогональной проекцией плоскости α на плоскость П₄ является прямая линия α₄. Точка 1 отмечена произвольно на фронтали f. Затем необходимо построить дополнительную ортогональную проекцию А₄ точки А на плоскость П₄ и из точки А₄ опустить перпендикуляр на прямую α₄. Длина отрезка [ А₄K₄ ] равна искомому расстоянию от точки А до плоскости α (h∩f), т.е. / А₄K₄ / = / АK /. Горизонтальная проекция [ А₁K₁ ] параллельна оси x₁₄, так как отрезок [ АK ] параллелен плоскости П₄, и перпендикулярна к горизонтальной проекции h₁ горизонтали h плоскости α. Фронтальная проекция А₂ K₂ построена перпендикулярно f_2.

Пример 9. Определить угол между пересекающимися прямыми l и m. Задача решена вращением вокруг горизонтали (рис.66).

Рис.66

Отмечаем в плоскости a(l Ç m) горизонталь h и поворачиваем плоскость вокруг горизонтали h в положение горизонтальной плоскости. При этом точки 1 и 2, принадлежащие горизонтали, остаются неподвижными. Точка А перемещается по окружности, плоскость которой перпендикулярна к горизонтали. На плоскость П₁ окружность проецируется в отрезок прямой, перпендикулярной к горизонтальной проекции h₁ горизонтали h. Проводим через горизонтальную проекцию А₁ точки А прямую, перпендикулярную к h₁, и отмечаем точку О₁, в которой она пересекает h₁. Точка О₁ - горизонтальная проекция центра О окружности, по которой перемещается точка А. Его фронтальная проекция О₂ принадлежит h₂. Отрезки О₁A₁ и О₂А₂ - горизонтальная и фронтальная проекции радиуса R_A указанной окружности. Отрезок ОА является отрезком общего положения.

Находим длину радиуса R_A, для чего строим дополнительную ортогональную проекции О₄А₄ отрезка ОА на плоскости П₄, проведенный через отрезок ОА и перпендикулярной к П₁.Отложив отрезок О₄А₄ на прямой О₁А₁ и от точки О₁, находим горизонтальную проекцию А¢₁ точки А после поворота. Соединив точку А¢₁ с точками 1₁ и 2₁, получаем проекции l ¢₁ и m¢₁ прямых l и m после поворота. Угол j° между ними равен искомому углу.

Пример 9. Определить угол между плоскостями a (а Ç b) и β (с Ç d) (рис.67).

Рис.67

Угол между двумя плоскостями равен углу между перпендикулярами к этим плоскостям.

Из произвольной точки пространства К(К₁, К₂) проведены перпендикуляры t (t₁ ^ a₁, t₂ ^ b₂) к плоскости a(а Ç b) и q(q₁ ^ c_1, q₂ ^ d₂) к плоскости β(с Ç d). Плоскость перпендикуляров t и q повернута вокруг фронтали f(f₁, f₂) до положения фронтальной плоскости. Фронтальные проекции t¢₂ и q¢₂ повернутых перпендикуляров t и q образуют угол j°, равный искомому углу между двумя плоскостями a и β.

 

Рис 68

Пример 10. Определить угол между прямой l и плоскостью a (h Ç f) (рис.66).

Рис.69

Углом между прямой и плоскостью является угол между этой прямой и её ортогональной проекцией на эту плоскость. Исходя из этого, решение задачи может быть следующим. Из произвольной точки М прямой l опускаем перпендикуляр n на плоскости a. Находим точку пересечения этого перпендикуляра с плоскостью (точка М_a) и точку К пересечения прямой l с плоскостью a. Через точки К и М_a проводим прямую l _a - проекцию прямой l на плоскости a. Угол j° между прямыми l и l _a - искомый угол.

Решение задачи упрощается, если определить угол ω° (угол между прямой l и перпендикуляром n). Зная угол ω°, определим искомый угол j°=90° - ω°. Для построения перпендикуляра n, на эпюре n₁ строится перпендикулярно к h₁, а n₂ строится перпендикулярно к f₂. Угол ω° между прямой l и перпендикуляром определяется поворотом плоскости этого угла вокруг горизонтали h*. Угол j° получается дополнением угла ω° до 90°(рис.70).

 

Рис.70