Прямая и точка в плоскости

Прямая принадлежит плоскости, если она имеет с ней две общие точки.Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости. Точка М принадлежит плоскости α (a ∩ b) (рис. 18), так как находится на прямой k, принадлежащей этой плоскости.

Прямая принадлежит плоскости, если проходит через одну точку плоскости и параллельна какой-нибудь прямой, лежащей в этой плоскости. Прямая k параллельна прямой АВ (рис. 19).

 

Рис. 18 Рис.19

 

Точка М принадлежит плоскости Δ АВС, так как находится на прямой k, принадлежащей заданной плоскости.

 

1.9. Главные линии плоскости – горизонталь и фронталь

Горизонталь плоскости. Это прямая, принадлежащая плоскости, и параллельная горизонтальной плоскости проекций (рис. 20а,б). Горизонталь обозначают буквой h. Построение горизонтали начинают с фронтальной проекции, так как она всегда параллельна оси х₁₂. Все горизонтали плоскости параллельны между собой.

 

 

а) б)

Рис.20

Фронталь плоскости. Это прямая, принадлежащая плоскости, и параллельная фронтальной плоскости проекций (рис. 21а, б). Фронталь обозначают буквой f. Построение фронтали всегда начинают с горизонтальной проекции, так как она всегда параллельна оси х₁₂. Все фронтали плоскости параллельны между собой.

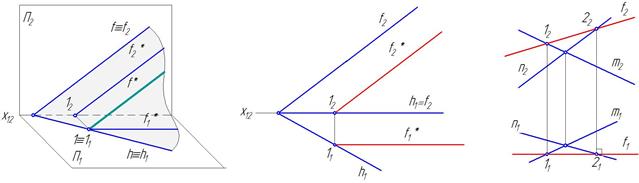
а) б)

Рис. 21

Пересечение плоскостей

Две плоскости пересекаются по прямой. Для нахождения проекций линии пересечения достаточно определить проекции двух общих точек, принадлежащих этим плоскостям.

Пример 1. Построить линию пересечения двух плоских фигур (рис.22)

Плоскость α (Δ АВС) частного положения (Δ АВС 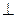П₁), плоскость β (Δ MNK ) – общего положения.

 

Рис.22

Поскольку Δ АВС является горизонтально-проецирующей плоскостью, линия пересечения плоскостей будет принадлежать горизонтальной проекции Δ АВС. Отметим общие горизонтальные проекции Q₁ и T₁ на пересечении горизонтальных проекций треугольников АВС и MNK. В проекционной связи отметим фронтальные проекции Q ₂ и T₂ в Δ M₂N₂K_{2 .} Линия пересечения QT определена фронтальной Q ₂T₂ и горизонтальной проекцией Q₁T₁.

Определим видимость плоских фигур, т.к. плоскости считаются непрозрачными. Видимость на горизонтальной плоскости проекций определять не надо, т.к. Δ АВС проецируется в прямую линию, следовательно проекция M₁N₁K₁ видима. Определим видимость плоских фигур на плоскости проекций П₂. Для этого рассмотрим точки 1 и 2, лежащие на скрещивающихся прямых ВС и МK. Фронтальные проекции 1₂ и 2₂ совпадают, а горизонтальная проекция 2₁ находится перед горизонтальной проекцией 1₁. Точка 2 видима относительно плоскости проекций П₂. Следовательно сторона B₂C₂ видима, фронтальная проекция Δ А₂В₂С₂ видима на П₂ с той стороны, где находятся точки 1₂ и 2₂. После фронтальной проекции линии пересечения Q₂T₂ становится видимым Δ MNK.

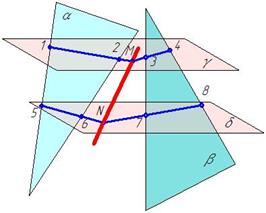
Пример 2. Построить линию пересечения плоскостей α (Δ АВС) и β (Δ DEF)(рис.23).

Проведем вспомогательную горизонтальную плоскость γ, пересекающую одновременно заданные плоскости α (Δ АВС) и β (Δ DEF),соответственно, по прямым 1-2 и 3-4. Прямые 1-2 и 3-4 пересекутся в точке М. Затем проведем еще одну горизонтальную плоскость δ. Прямая, проходящая через точку 5 параллельна прямой 1-2. Прямая, проходящая через точку 6 параллельна прямой 3-4. Получим точку N. Соединив точки М и N, получим искомую прямую МN. Решение задачи на эпюре показано на рис.23.

 

 

 

Рис.23