В общем случае указанная задача решается следующим образом. Через заданную прямую проводят вспомогательную плоскость и строят линию пересечения вспомогательной плоскости с поверхностью геометрического тела. Точки пересечения этих двух линий являются искомыми точками пересечения.
Пример 1. Построить точки пересечения прямой l с пирамидой. Определить видимость прямой (рис.45).
Через заданную прямую проведем вспомогательную плоскость частного положения. При пересечении гранной поверхности с плоскостью получается многоугольник, вершины которого находятся на ребрах. При пересечении этого многоугольника с заданной прямой l получим искомые точки.


Рис.45
Через прямую l проведем фронтально-проецирующую плоскость α^П 2, l2 ≡ α2 Строим линию пересечения плоскости α с поверхностью пирамиды. На фронтальной проекции отметим 12, 22, 32, в которых α2 пересекает проекции ребер. В проекционной связи отметим 11, 21 и 31. Соединяем горизонтальные проекции11,21,31 ломаной линией с учетом видимости. На горизонтальной плоскости проекций все грани пирамиды видимы. Следовательно, треугольник 11-21-31 видимый. На пересечении горизонтальной проекции l 1 с горизонтальной проекцией 11-21-31 отметим горизонтальные проекции M 1 и N 1 точек М и N. Строим фронтальные проекции M2 и N2 точек М и N на l2.
Определяем видимость прямой l. Между полученными точками M и N на обеихпроекциях прямая невидима всегда. Горизонтальная проекция l1 невидима только между M1N1. На плоскости П2: точка М находится на видимой грани AS B, следовательно, М2 видима и фронтальная проекция l2 видима до М2. Точка N принадлежит грани АSC, невидимой относительно П2. Следовательно, фронтальная проекция N2 невидима и фронтальная проекция l2 от N2 до ребра S2C2 невидима (рис.45.).
Пример 2. Построить точки пересечения прямой l с конусом. Определить видимость прямой (рис.46).
Для определения точек пересечения прямой с конусом целесообразно через прямую l провести плоскость, проходящую через вершину конуса S, которая пересечет поверхность конуса по образующим. Зададим плоскость α двумя пересекающимися прямыми l и m. Для определения образующих S4 и S5, по которым плоскость α пересекает поверхность конуса, построена линия 2–3 пересечения плоскости α с плоскостью основания конуса. На пересечении α1 с основанием конуса отметили 41 и 51 точек 4 и 5. Горизонтальные проекции образующих S141и S151 пересекаются с горизонтальной проекцией прямой l в точках М1 и N1, а затем по линиям связи отмечаем проекции М2 и N2 точек М и N.

Рис.46
Для определения видимости достаточно установить видимость точек пересечения ее с поверхностью. Если точка видна, то и прямая l видна; если точка не видна, то и прямая l не видна. Видимость точек определена по видимости образующих, проходящих через них. Точка N2 невидима, следовательно прямая l2 невидима до очерковой образующей.За очерком поверхности прямая видима всегда.
Пример 3. Построить точки пересечения прямой l со сферой (рис.47).
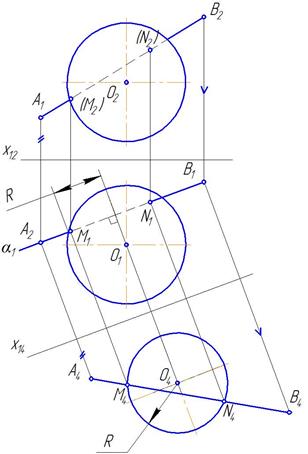
Рис.47
Проведем через прямую вспомогательную горизонтально-проецирующую плоскостью. Плоскость пересечет поверхность сферы по окружности, которая на плоскость П2 спроецируется в эллипс. Чтобы не строить эллипс, воспользуемся методом дополнительного проецирования на плоскость П4 – горизонтально-проецирующую и параллельную прямой l. Тогда линия пересечения спроецируется на П4 в окружность радиуса R. Построена дополнительная проекция прямой АВ. На пересечении отмечены дополнительные проекции точек М4 и N4. Затем построены горизонтальные и фронтальные проекции точек М и N. Видимость прямой l установлена по видимости точек М и N. Точка N расположена выше экватора сферы, т.е. на видимой относительно П1 половине сферы, а точка М – ниже экватора, т.е. на невидимой половине. Поэтому относительно П1 точка N- видима, а точка М – невидима (закрыта в скобки). Относительно П2 точки М и N невидимы, поскольку находятся за главным меридианом сферы (рис.47).
Пересечение поверхностей
Для построения линии пересечения двух поверхностей нужно найти ряд точек, общих для обеих поверхностей, и соединить полученные точки в определенной последовательности с учетом видимости.
Характер линии пересечения поверхностей зависит от формы поверхностей и их взаимного расположения. В общем случае линией персечения может быть:
а) пространственная ломаная линия – при пересечении многогранников
б) пространственная кривая – при пересечении двух кривых поверхностей или состоящая из отрезков плоских кривых при пересечении кривой поверхности и многогранника.
В некоторых случаях линия пересечения может быть плоской кривой –окружностью, эллипсом.
Пример 1. Построить линию пересечения цилиндра и усеченного конуса (рис.48).
Две кривые поверхности пересекаются по пространственной кривой.
Цилиндрическая поверхность является фронтально-проецирующей. Следовательно, фронтальная проекция линии пересечения совпадает с фронтальным очерком цилиндра – окружностью. Построим горизонтальную проекцию, исходя из условия принадлежности точек этой линии поверхности усеченного конуса.

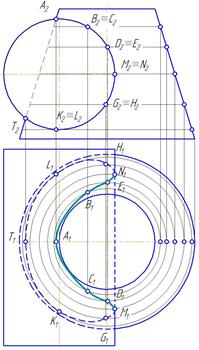
Рис.48
Отметим характерные точки – фронтальные проекции точек А2 и Т2 на пересечении фронтальных очерков цилиндра и усеченного конуса. Отметим фронтальные проекции M2, N2, в которых будет меняться видимость линии пересечения на горизонтальной плоскости проекций. Точки K2, L2 –низшие точки линии пересечения. Точки D2, E2, G2, H2 – точки изменения видимости на профильной плоскости проекций. В2,С2 – выбраны произвольно на фронтальном очерке цилиндра. Горизонтальные проекции точек, принадлежащих поверхности усеченного конуса находим на окружностях соответствующего радиуса. Соединим полученные точки плавной линией с учетом видимости. Точки, принадлежащие видимой части поверхности цилиндра относительно горизонтальной плоскости проекций, соединяем сплошной линией. В точках М1, N1, происходит изменение видимости. Определяем видимость горизонтальных и фронтальных очерков цилиндра и усеченного конуса (рис. 48).
Пример 2. Построить линию пересечения сферы с конусом (рис.49).
Обе кривые поверхности общего вида. У этих поверхностей имеется общая плоскость симметрии, поэтому линия пересечения будет симметрична относительно этой плоскости.
Отметим характерные точки линии пересечения. Точки А и В лежат на пересечении фронтальных очерков. Точки С и D найдем на пересечении экватора сферы a и окружности b поверхности конуса, лежащих в одной горизонтальной плоскости α. Аналогично могут быть найдены и другие точки линии пересечения. Так точки М и N строим как пересечение окружностей c и d, принадлежащих одной горизонтальной плоскости β.


Рис. 49
Полученные точки соединяем плавной кривой с учетом видимости. При установлении видимости следует помнить, что эта линия будет видима, если она принадлежит как поверхности сферы, так и конуса. Точки А и В отделяют видимую относительно фронтальной плоскости часть линии пересечения (она проходит через точки А, С, М, В) от невидимой. В данной задаче фронтальные проекции видимой и невидимой части линии пересечения совпадают.
Точки С и D отделяют видимую относительно горизонтальной плоскости часть линии пересечения от невидимой. Точка А видима относительно горизонтальной плоскости проекций, так как лежит выше экватора сферы. Следовательно, линия, проходящая через точки А, С, D – видима, остальная часть линии невидима. Определим видимость очерков конуса и сферы (рис.49).
Метрические задачи






