Одним из недостатков линейного регрессионного анализа является то, что он может быть применен только к линейным уравнениям.
Если между экономическими явлениями существуют нелинейные отношения, то они выражаются с помощью нелинейных функций.
а) параболы второго порядка (или высших порядков):
ўx =a + bx + cx2;
б) гиперболы:
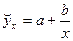 ;
;
в) показательной функции:
ўx = abx;
г) степенной функции:
ўx =axb;
д) экспоненциальной функции:
 .
.
Параметры нелинейной регрессии a и b также определяются с помощью метода наименьших квадратов, но процессу построения системы нормальных уравнений предшествует этап линеаризации кривой, предусматривающий переход от нелинейных связей к линейной зависимости изменения признака. С этой целью осуществляется замена переменных, исходя из соотношений, приведенных в таблице 8.1.
Таблица 8.1
| Функция | Исходное уравнение | Способы замены переменных | Линеаризованное уравнение | Система нормальных уравнений |
| Параболическая | ўx =a + bx + cx2 | - | - | ì Sy=na+bSx+сSx2, ï í Syx =aSx + bSx2 + сSx3, ï î Syx2 =aSx2 + bSx3 + сSx4, |
| Гиперболичес-кая | ўx = a + b/x | x1=1/x | ўx =a+bx1 | ì S y = an + bS x1 í î S y x = aS x1 + bS x12 |
| Логарифмичес-кая | ўx = a + bln x | x1= lnx | ўx =a+bx1 | ì S y = an + bS x1 í î S yx1 = aS x1 + bS x12 |
| Степенная | ўx = axb | 1. Логарифмируем уравнение: ln ўx = ln a + blnx 2. Обозначим: yt1= ln ўx a1 = ln a x1=lnx | yx1= a1 +b x1 | ì S y1 = a1 n + bS x1 í î S y1 x1 = a1Sx1 + bS x12 |
| Экспоненциальная | ўx = a ebx | 1. Логарифмируем уравнение: ln ўx = ln a + bx 2. Обозначим: yt1= ln ўx a1 = ln a | yx1= a1 +b x | ì S y1 = a1 n + bS x í î S y1x = a1S x + bS x2 |
На практике случаи, когда на результативный признак влияет только один факторный, встречаются очень редко. Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества факторов. Как правило, каждый фактор в отдельности не определяет изучаемое явление во всей полноте. Только комплекс факторов в их взаимосвязи может дать более или менее полное представление о характере изучаемого явления.
Например, при построении модели потребления того или иного товара от дохода необходимо учитывать такие факторы как цена товара, размер семьи, ее состав. Одновременное влияние этих факторов на зависимую переменную (потребление товара) можно изучить, построив уравнение множественной регрессии.
Многофакторный корреляционный анализ включает несколько этапов.
На первом этапе определяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются наиболее существенные для корреляционного анализа.
На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа.
На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, то есть подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. Например, линейное уравнение множественной регрессии:  .
.
На четвертом этапе проводится расчет основных показателей связи корреляционного анализа.
На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение.
Оценка параметров множественной регрессии вручную затруднительна и приводит к потерям точности, поэтому для ее построения и получения оценок параметров используют методы компьютерного анализа.






