Одной из важнейших задач статистики является определение в рядах динамики основной тенденции развития.
Основной тенденцией развития (трендом) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний.
Для выявления тенденции в рядах динамики используют специальные методы:
1. Метод укрупнения интервалов - предполагает переход от первоначального динамического ряда к рядам с большими временными промежутками, например, данные за каждый месяц года заменяют квартальными, годовые — пятилетними и т.д. По сформированным укрупненным интервалам либо просто суммируют уровни первоначального ряда, либо рассчитывают средние величины. В результате отклонения в уровнях первоначального ряда, обусловленные случайными причинами, сглаживаются, и более явно обнаруживается действие основных факторов (общая тенденция).
2. Метод скользящей средней – состоит в замене фактических значений показателя их усредненными величинами, расчет которых проводят путем последовательного смещения начала отсчета на единицу времени (скольжения), т.е. постепенно исключают из интервала первые уровни и включают последующие. Полученная средняя относится к середине укрупненного интервала.
Наиболее часто на практике применяются трехчленные средние:
.
Полученный таким образом сглаженный ряд более четко выражает основную тенденцию развития изучаемого явления.
3. Метод аналитического выравнивания – заключается в том, что находится уравнение 
, график которого наилучшим образом отражает основную тенденцию ряда динамики.
Аналитическое выравнивание позволяет не только определить основную тенденцию развития явления во времени, но и выполнять расчеты для таких периодов, по которым нет информации. При этом нахождение недостающих данных внутри динамического ряда называется интерполяцией, а нахождение значений за пределами анализируемого периода (т.е. в будущем) называется экстраполяцией.
Таким образом, на основе экстраполяции данных можно прогнозировать развитие явления в будущем, т.к. такое прогнозирование предполагает, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда.
Например, путем аналитического выравнивания получено, что основная тенденция явления выражается уравнением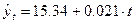 
. Зная это уравнение и подставляя в него значения t, находящиеся за пределами этого ряда, можно построить прогноз. Пусть t=11, тогда прогнозируемое значение будет равно 
.
Однако следует помнить, что в действительности тенденция развития того или иного явления не остается неизменной, поэтому полученные путем экстраполяции прогнозируемые значения следует рассматривать как вероятностные оценки.
