Для количественной оценки динамики проводят расчет таких показателей, как абсолютный прирост, темп роста, темп прироста, темп наращивания, абсолютное значение 1% прироста, средний уровень ряда динамики.
В основе расчета показателей ряда динамики лежит сравнительный анализ уровней ряда либо с постоянной, либо с переменной базой сравнения. При постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же показателем (уровнем), принятым за базу сравнения (у0). В этом случае получают базисные показатели. При переменной базе сравнения каждый уровень ряда сравнивают с предыдущим уровнем (yi-1) получают цепные показатели.
Таким образом, выделяют следующие аналитические показатели динамики:
1. Абсолютный прирост – это разность двух уровней ряда в исходных единицах измерения, которая характеризует абсолютное изменение уровня ряда за определенный промежуток времени:
- базисный: 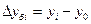 ;
;
- цепной: 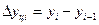 .
.
Абсолютный прирост может иметь отрицательное значение, если уровень изучаемого периода ниже уровня базисного периода или предшествующего.
Между цепными и базисным абсолютным приростом существует взаимосвязь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего уровня ряда динамики:
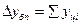
2. Темп роста – это отношение двух уровней ряда, выраженное в процентах. Он характеризует относительное изменение уровня динамического ряда за какой-либо период времени:
- базисный:  ;
;
- цепной: 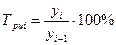 .
.
Если темп роста > 100%, то идет увеличение изучаемого уровня по сравнению с базисным или предыдущим показателем и наоборот.
Напомним, что средний темп роста определяется по формуле средней геометрической. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах (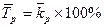 ), то средний темп роста определяется по формуле:
), то средний темп роста определяется по формуле:
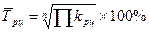 .
.
Между базисным и цепными коэффициентами роста существует взаимосвязь – произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста последнего уровня ряда динамики:
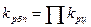 .
.
3. Темп прироста – характеризует абсолютный прирост в относительных величинах:
- базисный: 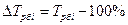 или
или 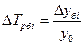 ;
;
- цепной: 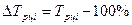 или
или 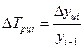 .
.
Если уровни ряда динамики сокращаются, то соответствующие показатели темпов прироста будут отрицательными, т.к. они характеризуют уменьшение ряда динамики в %.
Средний темп прироста определяется по формуле:
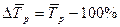 .
.
4. Темп наращивания – показывает в экономике наращивание во времени экономического потенциала. Вычисляется делением цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения:
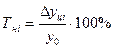 .
.
5. Абсолютное значение одного процента прироста – применяется для сравнения абсолютного прироста и темпа прироста за одни и те же периоды времени, и показывает, какое абсолютное значение скрывается за относительным показателем – одним процентом прироста:
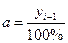 .
.
6. Средний уровень ряда динамики – характеризует обобщенную величину абсолютных уровней.
Методы расчета среднего уровня интервального и моментного рядов динамики различны.
Для интервальных рядов динамики средний уровень за период времени определяется по формуле средней арифметической:
а) при равных интервалах применяется средняя арифметическая простая:
 .
.
б) при неравных интервалах применяется средняя арифметическая взвешенная:
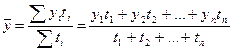 .
.
Средний уровень моментного ряда динамики с равноотстоящими датами определяется по формуле средней хронологической простой:
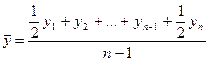 .
.
Для моментных рядов с неравноотстоящими датами расчет среднего уровня ряда производится по формуле средней хронологической взвешенной:
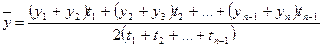 .
.






