Статистическое наблюдение может быть сплошным и несплошным.
Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности. Изучение не всех единиц совокупности, а лишь некоторой части, осуществляется с помощью несплошного наблюдения. Самым распространенным видом несплошного статистического наблюдения является выборочное наблюдение.
Выборочное наблюдение – это такое несплошное наблюдение, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных случайным образом, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.
На практике выборочное наблюдение применяют в тех случаях, когда изучаемая совокупность велика, и обследовать ее всю практически невозможно, или, когда наблюдение связано с порчей качества продукции (определение прочности нити, качества консервов, жирности молока и т.д.). Кроме того, выборочное наблюдение существенно экономит время, финансовые, материально-технические и трудовые ресурсы, и, как следствие, позволяет более детально исследовать отдельные единицы наблюдения. Благодаря этому, выборочное наблюдение находит широкое применение во всех сферах хозяйственной деятельности. Его используют в опросах общественного мнения, в исследованиях покупательского спроса, формирования доходов и структуры расходов населения, контроля качества продукции, контроля норм выработки и т.д.
Совокупность, из которой производится отбор, называется генеральной, а совокупность отобранных единиц – выборочной совокупностью или выборкой.
В статистике по способу отбора различают следующие виды выборок:
1. Собственно-случайная выборка – предполагает отбор единиц из генеральной совокупности посредством жеребьевки или другого подобного способа (например, тиражи выигрышей лотерейных билетов).
2. Механическая выборка – состоит в том, что отбор единиц в выборочную совокупность осуществляется из генеральной совокупности, разбитой на равные группы по нейтральному признаку, так, что из каждой группы в выборку попадает только одна единица.
3. Типическая выборка – используется, когда генеральная совокупность разбита на несколько однотипных групп по признакам, влияющим на изучаемые показатели, и из каждой типической группы производится индивидуальный отбор единиц в выборочную совокупность.
4. Серийная выборка – предполагает случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп (серий).
5. Комбинированная выборка.
При этом отбор единиц в выборочную совокупность может осуществляться двумя методами: повторным и бесповторным.
При повторном отборе попавшая в выборку единица подвергается обследованию, а затем возвращается в генеральную совокупность, где наравне с другими единицами участвует в дальнейшей процедуре отбора. На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков. Например, при проведении маркетинговых исследований мы не можем точно оценить, сколько покупателей предпочитает делать покупки именно в данном супермаркете и т.д. Поэтому возможно повторение единиц наблюдения по причине как практически неограниченных объемов совокупности, так и возможной повторной регистрации. Например, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.
При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.
Ошибки выборки
Любое выборочное наблюдение, как бы грамотно оно ни было организовано, всегда связано с определенными ошибками, которые делятся на два класса:
а) ошибки регистрации являются следствием неправильного установления значения наблюдаемого признака или неправильной записи, они характерны для всех видов наблюдения;
б) ошибки репрезентативности обусловлены тем, что выборочная совокупность не может в точности воспроизвести генеральную совокупность. При этом следует различать:
- систематические ошибки репрезентативности – преднамеренные, связанные с нарушением принципов формирования выборочной совокупности. Например, в выборку попали единицы, характеризующиеся большими (меньшими) по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными (заниженными).
- случайные – обусловлены действием случайных факторов.
Статистически можно оценить только случайные ошибки репрезентативности. Для этого с определенной степенью вероятности определяют величину предельной ошибки, с которой результаты выборочного обследования могут быть распространены на всю генеральную совокупность.
В зависимости от исходных данных и способа отбора единиц в выборку, величина предельной ошибки определяется по формулам, приведенным в таблице 5.1.
Таблица 5.1
 Метод отбора
Вид выборки
| Повторный | Бесповторный | ||
| для среднего значения | для доли | для среднего значения | для доли | |
| Собственно-случайная и механическая | 
| 
| 
| 
|
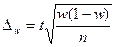
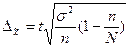
| Типическая | 
| 
| 
| 
|
| Серийная |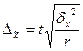 
| 
| 
| 
|
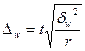
Основные обозначения:
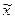- выборочная средняя;
w – выборочная доля - определяется отношением числа единиц, обладающих изучаемым признаком m, к общему числу единиц в выборке n: 
;
n – число единиц в выборочной совокупности;
N – число единиц в генеральной совокупности;
r – число отобранных серий;
R – общее число серий;
t – величина нормированного отклонения, значение которого соответствует определенному уровню вероятности p (табл. 5.2).
Таблица 5.2
