С точки зрения кибернетики система – это множество, на котором реализуется заранее данное отношение R с фиксированными свойствами P. Таким образом, если имеется множество элементов M, на котором обнаруживаются какие-то произвольные отношения R, то это множество не обязательно будет определяться как система. Системой его можно назвать лишь в том случае, когда на множестве элементов M будет выполняться некоторое определенное, фиксированное отношение, например, связи или порядка.
Упорядоченность – характеристика системы, отражающая наличие определенным образом установленных взаимосвязей.
Для описания состояния и движения системы можно применять такие широко распространенные способы, как словесное описание, табличное или матричное описание, математические выражения, графические способы. Однако наиболее адекватной является формализованная геометрическая интерпретация состояния и движения систем в так называемом пространстве состояний или фазовом пространстве.
Пространством состояния системы называется пространство, каждой точке которого однозначно соответствует определенное состояние рассматриваемой динамической системы, а каждому процессу изменения состояний системы соответствует определенная траектория перемещения изображающей точки в пространстве.
В том случае, когда состояние системы можно охарактеризовать только одним параметром, то фазовое пространство будет одномерным и просматриваться в виде участка оси x, на котором точка х1 соответствует состоянию системы в момент времени t (рис. 5.1).

Рис. 5.1. Геометрическое изображение состояний системы в одномерном
и двумерном фазовом пространстве
Если состояние системы характеризуется двумя параметрами, то фазовое пространство будет двумерным.
В тех случаях, когда состояние системы описывается тремя параметрами, оно будет изображаться точкой в трехмерном пространстве, а траектория движения системы – пространственной кривой в этом пространстве.
В общем случае, когда число параметров, характеризующих систему, произвольно и, как в большинстве сложных экономических систем, значительно больше трех, геометрическая интерпретация теряет наглядность. Однако геометрическая терминология и в этих случаях остается удобной для описания состояния и движения систем в так называемом n -мерном или многомерном фазовом пространстве (гиперпространстве).
В реальных условиях работы системы ее параметры, как правило, могут изменяться в некоторых ограниченных пределах. Область фазового пространства, за пределы которой не может выходить параметр системы, называется областью допустимых состояний системы (рис. 5.2).
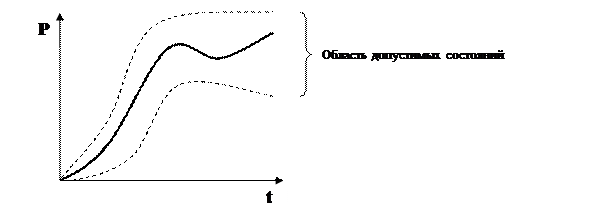
Рис. 5.2. Границы области допустимых состояний системы
При исследовании и проектировании систем всегда исходят из того, что система должна оставаться в пределах области ее допустимых состояний.






