Теоретический закон распределения. Метод моментов

При исследовании случайной величины Х по результатам её испытаний часто требуется найти закон её распределения. Тип распределения можно угадать по виду гистограммы или полигона. Будем называть выбранное нами распределение теоретическим. Каждое теоретическое распределение содержит один или более параметров a₁, a₂, …, a_S, которым должны быть присвоены некоторые значения. Например, экспоненциальное распределение с плотностью вероятностей f(x) = lexp(-lx) содержит один параметр l, а нормальное распределение с плотностью

f(x) =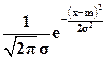

содержит два параметра m и s. Параметры теоретического распределения нужно выбирать, очевидно, так, чтобы полученное распределение как можно лучше согласовывалось с опытными данными, то есть с выборкой. Другими словами, теория должна как можно точнее описывать эксперимент. Одним из способов выбора параметров теоретического распределения является метод моментов: параметры a₁, a₂, …, a_k выбираются так, чтобы k первых моментов теоретического распределения совпадали с их выборочными оценками.

Рассмотренные нами в начале параграфа распределения содержат один или два параметра. Первыми двумя моментами являются математическое ожидание и дисперсия. Поэтому метод моментов в нашем случае сводится к такому выбору одного или двух параметров теоретического распределения, чтобы выполнялось первое или или равенства:

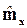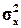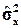
m_x = ; = , (1.24)

 

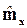где и 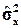– оценки математического ожидания и дисперсии по выборке.

Например, в случае экспоненциального распределения имеется только один параметр l, при этом m_x = и из первого равенства (1.24) получаем l = 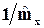. В случае же нормального распределения параметров два, при этом m_x = m и 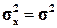, поэтому из обоих равенств (1.24) получаем два параметра: и .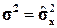

Отметим, что метод моментов является лишь одним из возможных методов определения параметров теоретического распределения. Для некоторых типов распределений он может дать плохие результаты. Рассмотрим, например, равномерное распределение с плотностью 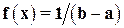, x Î[a, b]. Его параметры a и b связаны с m_x и 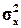равенствам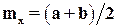и и 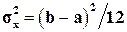. Метод моментов приводит к системе уравнений:

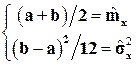
Может случиться, что найденная из этой системы нижняя граница распределения a, окажется больше некоторых значений из выборки, или же верхняя граница b окажется меньше некоторых выборочных значений. Теоретическое распределение с такими параметрами a и b следует сразу же отвергнуть как противоречащее условию, что все значения Х должны принадлежать отрезку [a, b].

В случае равномерного распределения следует выбирать значения:

 

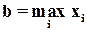; , (1.25)

 

которые не приводят к описанным выше противоречиям. Если имеется группированная выборка, то а – левая граница первого разряда, b – правая граница последнего разряда.

Аналогичным образом можно определить некоторые из параметров других ограниченных распределений. Рассмотрим, например, смещённое экспоненциальное распределение с плотностью:

 

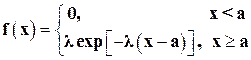(1.26)

сосредоточенное на интервале (а, ¥). Параметр сдвига а определяется из первого соотношения (1.25), а для определения l используем метод моментов, приравнивая математические ожидания: 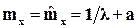, откуда .

 

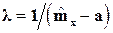Критерии согласия.

Относительно имеющейся выборки S могут быть высказаны какие–то предположения или гипотезы. Например, мы можем выдвинуть гипотезу о том, что исследуемая случайная величина Х имеет нормальное распределение. Методы проверки гипотез в математической статистике называют критериями.

В общем случае проверка гипотезы производится следующим образом. Пусть относительно выборки S выдвинута гипотеза Н₀. Критерием является некоторая функция U = U (S, H₀). Вся область значений D критерия U делится на две области D₀ и D₁. Если вычисленное значение критерия принадлежит области D₀, то гипотеза H₀ принимается, в противном случае Н₀ отвергается. Область D₀ называется областью допустимых значений или областью принятия гипотезы, область D₁ называется областью отклонения гипотезы или критической областью.

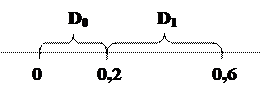Поясним это следующим примером. Пусть выдвинута гипотеза Н₀, что вероятность события А равна 0,6. В серии же из 100 опытов событие произошло m раз. В качестве критерия примем функцию U = | m/100–0,6|, то есть отклонение относительной частоты события А в серии из 100 испытаний от предлагаемой вероятности 0,6. Множество значений D критерия есть отрезок [0; 0,6]. Естественно принимать гипотезу Н₀, если m/100 не слишком отличается от 0,6 и отвергать, если разница велика, например, превышает 0,2. Таким образом, Н₀ принимается, если значение U = |m/100–0,6| £ 0,2, и отвергается, если U > 0,2. Для этого примера области D₀ и D₁ показаны на рис.1.8.

Рис.1.8. Допустимая и критическая области принятия решения.

 

Выборка S является случайной, поэтому и U(S, H₀) является случайной величиной. Следовательно, принятие или отклонение гипотезы – случайные события и при проверке гипотез возможны следующие ошибки.

1. Гипотеза верна, но отвергается (ошибка первого рода).

2. Гипотеза неверна, но принимается (ошибка второго рода).

Вероятность b ошибки первого рода называют уровнем значимости критерия. Таким образом, уровень значимости есть вероятность отвергнуть истинную гипотезу.

Если 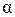-вероятность ошибки второго рода, то 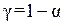называется мощностью критерия. Это вероятность отвержения неверной гипотезы.

 

Вероятности обеих ошибок желательно минимизировать, но оказывается, что попытка уменьшить вероятность одной ошибки приводит к увеличению вероятности другой. Поэтому вероятность одной из ошибок задаётся, а вероятность второй ошибки стараются сделать минимальной.

Чаще всего для проверки гипотез о законах распределения применяется критерий согласия χ ² (хи-квадрат), предложенный К.Пирсоном. Рассмотрим этот критерий.

Пусть имеется группированная выборка S и выдвинута гипотеза H₀, что случайная величина Х имеет функцию распределения F(x). Если бы гипотеза Н₀ была верна, то вероятность попадания значения Х в i –ый частичный интервал [a_i; a_i+1] была бы равна

P_i = F(a_i+1) – F(a_i), (1.27)

 

а математическое ожидание числа попаданий Х в этот полуинтервал, то есть ожидаемая или теоретическая частота была бы равна

 

n_i = nР_i, (1.28)

 

где n = m₁ + m₂ + … + m_k. Критерий χ ² оценивает меру расхождения теоретических nP_i и статистических (или выборочных) частот m _i:

 

χ ² = 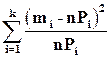. (1.29)

 

Чем больше отличаются m_i от nP_i, тем больше значение χ ²

К.Пирсон доказал, что при истинности H₀ распределение случайной величины (1.29) при n®¥ неограниченно приближается к так называемому c² – распределению, независимо от вида распределения F(x). Это приближение к c² – распределению можно считать удовлетворительным, если все частоты m _i достаточно велики. Будем поэтому предполагать, что все m_i ≥ 6.

Следует отметить, что между теоретическими частотами n_i = nP_i и статистическими частотами m_i имеются некоторые связи. Одна связь имеется всегда:

 

n₁ + n₂ + … + n_k = m₁ + m₂ + … + m_k = n. (1.30)

Другие связи появляются при оценке параметров теоретического распределения по выборке. Если, например, приравнены теоретическое и выборочное среднее, то имеется одна дополнительная связь. Если приравнены ещё и дисперсии, то дополнительных связей будет две. Эти связи приводят к зависимости слагаемых в выражении (1.29) между собой.

Наличие связей учитывается определением числа независимых слагаемых в выражении (1.29), называемом числом степеней свободы, которое определяется по формуле:

 

r = k – 1 – s, (1.31)

 

где k – число частичных интервалов группированной выборки, s – число дополнительных связей (кроме связи (1.30)) между теоретическим распределением и выборкой. Число s равно количеству параметров теоретического распределения, определённых именно по выборке. В это число не входят параметры, определённые по каким – либо соображениям независимо от выборки. Например, может быть известно заранее, что X имеет нулевое математическое ожидание. Тогда при гипотезе о нормальном распределении будет наложена только одна дополнительная связь – приравниваются теоретическая и выборочная дисперсии. Дополнительных связей может и вообще не быть (s = 0), если, к примеру, без предварительного анализа выборки (или даже до её получения) выдвинуть гипотезу о теоретическом распределении с фиксированными значениями входящих в него параметров.

Распределение вероятностей типа c² полностью определяется числом степеней свободы r, в зависимости от которого составляются таблицы этого распределения, и F_r(x) – функция распределения случайной величины c² с r степенями свободы.

Пусть число степеней свободы r определено. Допустим, что c²_b удовлетворяет равенству: F_r(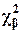) = 1 – b. Это означает, что:

 

P(c² > 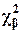) = b, (1.32)

 

то есть вычисленное по формуле (1.29) значение c² (в случае истинности гипотезы Н₀) превосходит значение 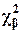с вероятностью b.

Таким образом, если гипотезу Н₀ принимать в случае c² £ 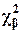и отвергать при c²> 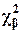, то верная гипотеза Н₀ будет отвергаться с вероятностью b, то есть b является уровнем значимости сформулированного критерия. Критические значения 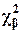даны в приложении 2в зависимости от уровня значимости b и числа степеней свободы r.

Итак, применение критерия c² сводится к следующему. Выбирается (или задаётся) уровень значимости b. По группированной выборке с частотами m_i не менее шести вычисляется значение c² по формуле (1.29). По найденному числу степеней свободы r и заданному b находится критическое значение 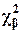из таблицы в приложении 2. Применяется решающее правило:

 

c² £ 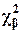® H₀ принимается,

(1.33)

c² > 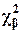® H₀ отвергается.

Если в имеющейся группированной выборке встречаются частоты, которые меньше шести, то следует объединить некоторые соседние интервалы, чтобы все частоты m_i были не менее шести.

Если некоторая гипотеза о теоретическом распределении F(x) в результате применения критерия была принята, F(x) может использоваться в дальнейшем для решения различных задач о случайной величине Х (но до тех пор, пока не будут получены экспериментальные данные, которым гипотеза Н₀ противоречит). Если же Н₀ оказалась отвергнутой, то следует подобрать и проверить гипотезу о другом теоретическом распределении, которая выглядит достаточно правдоподобно на фоне имеющихся экспериментальныхданных.

Замечание. Если гипотеза H₀ оказалось принятой, то это еще не значит, что она верна, так как имеется некоторая вероятность ошибки второго рода. Гипотеза H₀ принята не потому, что она верна (так это или не так, нам неизвестно), а потому, что она выглядит правдоподобной при имеющейся выборке S. Аналогично, если гипотеза H₀ отвергнута, то не следует категорически утверждать, что она ложна, так как возможна ошибка первого рода (отвергнуть верную гипотезу). Уровень значимости β и есть вероятность такой ошибки. Мы отвергаем гипотезу потому, что она выглядит неправдоподобной при имеющихся наблюдениях, т.е. выборке S. Напомним, что ошибки в проверке гипотез проистекают из-за случайности значений выборки, что связано с тем, что эти значения – результаты испытаний случайной величины.

Следует отметить, что определяемое по данному уровню значимости критическое значение 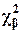содержит некоторую погрешность, так как распределении величины (1.29) несколько отличается от распределения c². Это отличие вызвано конечностью объёма выборки и способом выбора значений параметров теоретического распределения. Более корректным в данной ситуации является метод минимума c², состоящий в том, что параметры теоретического распределения выбираются так, чтобы величина (1.29) приняла минимально возможное значение. Однако этот метод трудно реализуем и поэтому применяется редко.