Важнейшими числовыми характеристиками случайной величины Х являются её математическое ожидание mx=M[x ] и дисперсия σ2x= D[x] = M[(X – mx)2] = M[x2] –  . Число mx является средним значением случайной величины, около которого разбросаны значения величин Х, мерой этого разброса являются дисперсия D[x] и среднеквадратическое отклонение:
. Число mx является средним значением случайной величины, около которого разбросаны значения величин Х, мерой этого разброса являются дисперсия D[x] и среднеквадратическое отклонение:
sx =  (1.11)
(1.11)
Мы будем в дальнейшем рассмотривать важную задачу для исследования наблюдаемой случайной величины. Пусть имеется некоторая выборка (будем обозначать её S) случайной величины Х. Требуется по имеющейся выборке оценить неизвестные значения mx и 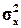 .
.
Теория оценок различных параметров занимает в математической статистике значительное место. Поэтому рассмотрим сначала общую задачу. Пусть требуется оценить некоторый параметр a по выборке S. Каждая такая оценка a* является некоторой функцией a*=a*(S) от значений выборки. Значения выборки случайны, поэтому и сама оценка a* является случайной величиной. Можно построить множество различных оценок (то есть функций) a*, но при этом желательно иметь «хорошую» или даже «наилучшую», в некотором смысле, оценку. К оценкам обычно предъявляются следующие три естественных требования.
1. Несмещённость. Математическое ожидание оценки a* должно равняться точному значению параметра: M[a*] = a. Другими словами, оценка a* не должна иметь систематической ошибки.
2. Состоятельность. При бесконечном увеличении объёма выборки, оценка a* должна сходиться к точному значению, то есть при увеличении числа наблюдений ошибка оценки стремится к нулю.
3. Эффективность. Оценка a* называется эффективной, если она не смещена и имеет минимально возможную дисперсию ошибки. В этом случае минимален разброс оценки a* относительно точного значения и оценка в определённом смысле является «самой точной».
К сожалению, не всегда удаётся построить оценку, удовлетворяющую всем трём требованиям одновременно.
Для оценки математического ожидания чаще всего применяется оценка.
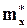 =
=  , (1.12)
, (1.12)
то есть среднее арифметическое по выборке. Если случайная величина X имеет конечные mx и sx, то оценка (1.12) не смещена и состоятельна. Эта оценка эффективна, например, если X имеет нормальное распределение (рис.п.1.4, приложение 1). Для других распределений она может оказаться неэффективной. Например, в случае равномерного распределения (рис.п.1.1, приложение 1) несмещённой, состоятельной оценкой будет
 (1.13)
(1.13)
В то же время оценка (1.13) для нормального распределения не будет ни состоятельной, ни эффективной, и будет даже ухудшаться с ростом объёма выборки.
Таким образом, для каждого типа распределения случайной величины Х следовало бы использовать свою оценку математического ожидания. Однако в нашей ситуации тип распределения может быть известен лишь предположительно. Поэтому будем использовать оценку (1.12), которая достаточно проста и имеет наиболее важные свойства несмещённости и состоятельности.
Для оценки математического ожидания по группированной выборке используется следующая формула:
 =
= 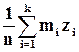 , (1.14)
, (1.14)
которую можно получить из предыдущей, если считать все mi значений выборки, попавших в i –й интервал, равными представителю zi этого интервала. Эта оценка, естественно, грубее, но требует значительно меньшего объёма вычислений, особенно при большом объёме выборки.
Для оценки дисперсии чаще всего используется оценка:

 =
=  , (1.15)
, (1.15)
Эта оценка не смещена и состоятельна для любой случайной величины Х, имеющей конечные моменты до четвёртого порядка включительно.
В случае группированной выборки используется оценка:
 =
=  (1.16)
(1.16)
Оценки (1.14) и (1.16), как правило, смещены и несостоятельны, так как их математические ожидания и пределы, к которым они сходятся, отличны от mx и 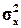 в силу замены всех значений выборки, попавших в i –й интервал, на представителя интервала zi.
в силу замены всех значений выборки, попавших в i –й интервал, на представителя интервала zi.
Отметим, что при больших n, коэффициент n /(n – 1) в выражениях (1.15) и (1.16) близок к единице, поэтому его можно опустить.
Интервальные оценки.
Пусть точное значение некоторого параметра равно a и найдена его оценка a*(S) по выборке S. Оценке a* соответствует точка на числовой оси (рис.1.5), поэтому такая оценка называется точечной. Все оценки, рассмотренные в предыдущем параграфе, точечные. Практически всегда, в силу случайности
a* ¹ a, и мы можем надеяться только на то, что точка a* находится где–то вблизи a. Но насколько близко? Любая другая точечная оценка будет иметь тот же недостаток – отсутствие меры надёжности результата.
 |
Рис.1.5. Точечная оценка параметра.
Более определённым в этом отношении являются интервальные оценки. Интервальные оценка представляет собой интервал Ib = (a, b), в котором точное значение оцениваемого параметра находится с заданной вероятностью b. Интервал Ib называется доверительным интервалом, а вероятность b называется доверительной вероятностью и может рассматриваться как надёжность оценки.
Доверительный интервал состоится по имеющейся выборке S, он случаен в том смысле, что случайны его границы a(S) и b(S), которые мы будем вычислять по (случайной) выборке. Поэтому b есть вероятность того, что случайный интервал Ib накроет неслучайную точку a. На рис. 1.6. интервал Ib накрыл точку a, а Ib* - нет. Поэтому не совсем правильно говорить, что a « попадает» в интервал.
Если доверительная вероятность b велика (например, b = 0,999), то практически всегда точное значение a находится в построенном интервале.
 |
Рис.1.6. Доверительные интервалы параметра a для различных выборок.
Рассмотрим метод построения доверительного интервала для математического ожидания случайной величины Х, основанный на центральной предельной теореме.
Пусть случайная величина Х имеет неизвестное математическое ожидание mx и известную дисперсию 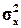 . Тогда, в силу центральной предельной теоремы, среднее арифметическое:
. Тогда, в силу центральной предельной теоремы, среднее арифметическое:
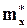 =
=  , (1.17)
, (1.17)
результатов n независимых испытаний величины Х является случайной величиной, распределение которой при больших n, близко к нормальному распределению со средним mx и среднеквадратическим отклонением  . Поэтому случайная величина
. Поэтому случайная величина
 (1.18)
(1.18)
имеет распределение вероятностей, которое можно считать стандартным нормальным с плотностью распределения j(t), график которой изображён на рис.1.7 (а также на рис.п.1.4, приложение 1).
 |
Рис.1.7. Плотность распределения вероятностей случайной величины t.
Пусть задана доверительная вероятность b и tb -число, удовлетворяющее уравнению
b = Ф0(tb) – Ф0(-tb) = 2 Ф0(tb), (1.19)
где  - функция Лапласа. Тогда вероятность попадания в интервал (-tb, tb) будет равна заштрихованной на рис.1.7. площади, и, в силу выражения (1.19), равна b. Следовательно
- функция Лапласа. Тогда вероятность попадания в интервал (-tb, tb) будет равна заштрихованной на рис.1.7. площади, и, в силу выражения (1.19), равна b. Следовательно
b = P(-tb <  < tb) = P(
< tb) = P( 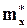 – tb
– tb  < mx <
< mx < 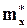 + tb
+ tb  ) =
) =
= P( 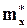 – tb
– tb  < mx <
< mx < 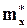 + tb
+ tb  ). (1.20)
). (1.20)
Таким образом, в качестве доверительного интервала можно взять интервал
Ib = ( 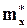 – tb
– tb  ;
; 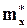 + tb
+ tb  ), (1.21)
), (1.21)
так как выражение (1.20) означает, что неизвестное точное значение mx находится в Ib с заданной доверительной вероятностью b. Для построения Ib нужно по заданному b найти tb из уравнения (1.19). Приведём несколько значений tb, необходимых в дальнейшем [3, 5]:
t0,9 = 1,645; t0,95 = 1,96; t0,99 = 2,58; t0,999 = 3,3.
При выводе выражения (1.21) предполагалось, что известно точное значение среднеквадратического отклонения sх. Однако оно известно далеко не всегда. Воспользуемся поэтому его оценкой (1.15) и получим:
Ib = ( 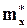 – tb
– tb 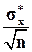 ;
; 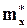 + tb
+ tb 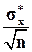 ). (1.22)
). (1.22)
Соответственно, оценки 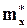 и
и 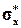 , полученные по группированной выборке, дают следующую формулу для доверительного интервала:
, полученные по группированной выборке, дают следующую формулу для доверительного интервала:
Ib = (  – tb
– tb  ;
;  + tb
+ tb  ). (1.23)
). (1.23)
Отметим, что формула (1.22) имеет две погрешности. Первая связана с тем, что распределение величины t лишь приближённо равно j(t), но с ростом объёма выборки n точность приближения улучшается. Вторая погрешность обусловлена использованием 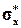 вместо неизвестного точного значения sх. При большом объёме выборки и эта погрешность несущественна. Формула (1.23) использует группированную, то есть огрубленную выборку, поэтому и даёт результат, остающийся огрублённым и при бесконечном росте объёма выборки.
вместо неизвестного точного значения sх. При большом объёме выборки и эта погрешность несущественна. Формула (1.23) использует группированную, то есть огрубленную выборку, поэтому и даёт результат, остающийся огрублённым и при бесконечном росте объёма выборки.
Следует отметить также, что можно построить сколько угодно доверительных интервалов для заданного b. Действительно, пусть t’b и t”b удовлетворяет условию b = Ф0(t”b) - Ф0(t’b), тогда интервал
Ib = ( 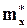 + t’b
+ t’b  ;
; 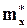 + t”b
+ t”b  ),
),
также с вероятностью b содержит mx (рис.1.7.). Например, можно взять t’0,9 = - 4 и t”0,9 = 1,282. Но в этом случае длина полученного интервала увеличится примерно в 1,6 раза. Формула (1.21) используется потому, что она даёт кратчайший доверительный интервал.
Аналогичным образом могут быть найдены интервальные оценки других параметров, например, дисперсии [1, 5].






