УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Методические указания к типовому расчёту по математической статистике
Ульяновск
Математическая статистика: Методические указания к типовому расчёту по курсу «Теория вероятностей и математическая статистика» / Сост. В.Р. Крашенинников, М.Н. Служивый. – Ульяновск: УлГТУ, 2012. – 41 с.
Настоящие методические указания составлены в соответствии с программой курса «Теория вероятностей и математическая статистика» для бакалавриата инженерно–технических специальностей высших учебных заведений. Изложена методика выполнения типового расчёта по математической статистике, дан образец его выполнения и приведены необходимые справочные данные.
Ил. 19. Табл. 11. Библиограф.: 6 назв.
Ó Ульяновский государственный технический университет, 2012
СОДЕРЖАНИЕ
1. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ ……………………4
1.1. Введение……………………………………………………………………4
1.2. Выборка. Вариационный ряд. Группированная выборка……………….……………………………………………………5
1.3. Статистическая функция распределения. Гистограмма. Полигон………………………………………………………………….…7
1.4. Оценки математического ожидания и дисперсии……………………...10
1.5. Интервальные оценки………………………………………………..…..12
1.6. Теоретический закон распределения. Метод моментов……...…..…...15
1.7. Критерии согласия……………………………………….………………17
1.8. Линейная среднеквадратическая регрессия………………….………...21
2. ЗАДАНИЕ ТИПОВОГО РАСЧЁТА …….….…………………….………...25
3. КОНТРОЛЬНЫЕ ВОПРОСЫ ……………………………… ……………...26
4. ПРИМЕР ВЫПОЛНЕНИЯ ТИПОВОГО РАСЧЁТА …………………….26
ПРИЛОЖЕНИЕ 1. Типовые законы распределения случайных величин.37
ПРИЛОЖЕНИЕ 2. Критические точки распределения…………………...40
ПРИЛОЖЕНИЕ 3. Функция Лапласа …………………...44
СПИСОК ЛИТЕРАТУРЫ ……..……………………………………………..46
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ.
Введение.
Значения многих величин, встречающихся в практической деятельности, зависят от ряда случайных факторов. Поэтом нельзя указать заранее, какое значение примет такая величина, так как оно меняется случайным образом от опыта к опыту. Такие величины называются случайными и изучаются в теории вероятностей. Например, случайными величинами являются: ёмкость изготовленного конденсатора, диаметр выточенного вала, уровень помех в канале связи и так далее. Случайная величина X полностью определяется в теоретико-вероятностном смысле своей функцией распределения вероятностей:
,
которая при любом x равна вероятности события X < x. Если Fx(x) известна, то применение методов теории вероятностей позволяет решить ряд задач, связанных с величиной X. В частности, вероятность попадания X в полуинтервал [a, b) может быть найдена по формуле:
P(a < X < b) = Fx(b) – Fx(a).
Таким образом, возникает задача нахождения функции распределения исследуемой случайной величины X. Иногда Fx(x) может быть найдена чистотеоретически из анализа природы величины X, но такие случаи относительно редки. В данных методических указаниях будет рассмотрена одна из основных задач математической статистики – нахождение Fx(x) по результатам наблюдений случайных величин.
Для описания многих явлений оказывается недостаточно одного параметра, поэтому приходится рассматривать два и более параметров и исследовать соотношения между ними. В некоторых случаях эти соотношения можно считать в определённых пределах точными, например, законы Ньютона, Ома и так далее. В других случаях такой определённости нет, например, точной зависимости между ростом и весом человека. Однако наблюдается приблизительная зависимость: «в среднем, с увеличением роста X увеличивается и вес Y», что может быть описано приближённой формулой:
y = ax + b.
Константы a и b при этом нужно подобрать так, чтобы приведённое выражение описывало как можно точнее связь между случайными величинами X и Y.
Таким образом, возникает ещё одна задача математической статистики – нахождение приблизительных, выполняющихся «в среднем», связей между случайными величинами. В данных методических указаниях будет рассмотрена задача определения, по результатам наблюдений величин X и Y, «наилучших»значений a и b в формуле y = ax + b.
Выборка. Вариационный ряд. Группированная выборка.
Предположим, что исследуется некоторое явление, описываемое двумя количественными признаками X и Y, которые буем считать случайными величинами. Требуется на основании ряда наблюдений охарактеризовать X и Y, а также оценить связь между ними.
Статистическое исследование начинается со сбора данных. Для этого производится n опытов (наблюдений), результаты которых регистрируются. Если (xi, yi) – значения X и Y, полученные в i –м опыте, то получаем последовательность:
(x1 , y1), (x2 , y2), …..., (xn, yn), (1.1)
называемую выборкой. Число опытов n называется объёмом выборки. Выборка является исходным материалом для всех дальнейших статистических выводов о случайных величинах X и Y.
Для начала будем исследовать X и Y по отдельности, поэтому сформируем из совместной выборки (1.1) две выборки для X и Y раздельно:
x1 , x2 , …, xn, (1.2)
y1, y2 , …, yn, (1.3)
На этом этапе обе выборки будут обрабатываться совершенно одинаково, поэтому рассмотрим только случайную величину X и её выборку (1.2).
Если элементы выборки (1.2) записать в порядке их возрастания, то полученная последовательность будет называться вариационным рядом. Вариационный ряд значительно удобнее для дальнейшей обработки, чем неупорядоченная (простая) выборка (1.2).
При большом объёме n простая выборка и вариационный ряд становятся очень громоздкими и мало наглядными. Для придания им большей наглядности и компактности производится группировка данных. Для этого весь интервал значений выборки разбивают на k частичных интервалов или разрядов и подсчитывают число mi значений выборки, попавших в каждый i –й разряд 
. Значение xg относится к i – му интервалу, если 
. Числа mi называются частотами. Результат этой группировки сводится в таблицу 1, называемую группированной выборкой. Первые три колонки этой таблицы и представляют нашу группированную выборку. В дальнейшем нам также понадобятся представители интервалов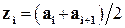 
, то есть средние точки интервалов, относительные частоты 
и плотности относительных частот 
. Для контроля правильности вычислений следует проверить равенства:
; 
.
Относительная частота 
равна доле элементов выборки, попавших в i –й интервал, поэтому числа дают более наглядное представление о выборке, чем частоты mi.
При всех своих положительных качествах, группированная выборка является некоторым огрублением статистического материала, так как известно только, что mi значений выборки находятся между ai и ai+1, точные же значения становятся неизвестными. Поэтому и вводится представитель интервала z i, который принимается за «среднее» значение элементов выборки из этого интервала.
Для того, чтобы огрубление не было слишком сильным, нужно стремиться делать частичные интервалы как можно короче, то есть увеличивать их количество. При этом следует соблюдать меру, так как при большом числе интервалов и группированная выборка сможет стать слишком громоздкой. Как правило, более 20 интервалов не используется. При объёме выборки порядка 100 следует взять 8 – 10 интервалов.
Таблица 1. Группированная выборка.
| Номер интервала | Границы интервала (ai ; ai+1) | Частотa m i | Представитель интервала z i | Относительная частота
| Плотность относительной частоты 
|
| (a1 ; a2 ) | m 1 | z 1 | 
| 
| |
| …………… | …………… | …………… | …………… | …………… | …………… |
| K | (ak; ak+1) | m k | z k | 
| 
|
Замечание. При подсчёте частот mi следует учитывать способ получения выборки. Пусть, например, производится округление до ближайшего деления в одну сотую, тогда элемент выборки xg = 6,50 должен восприниматься как число от 6,495 до 6,505. Если при этом 6,50 является границей интервалов, то становится неясным, к какому из двух соседних интервалов отнести xg = 6,50. Учитывая, что шансы попасть в любой из этих двух интервалов, равны, общее число r значений выборки, равных 6,50, делят между интервалами поровну (если r нечётно, то в какой-нибудь интервал относят на одно значение больше). Если же округление производится до сотых путём отбрасывания остальных значащих цифр, то xg = 6,50 должно восприниматься как число от 6,50 до 6,51 с соответствующими выводами при подсчёте частот.
