Статистической функцией распределения величины X по имеющейся выборке называется функция 
, равная относительной частоте события (X< x), то есть
, (1.4)
где nx – число значений в выборке, меньших x; n – объём выборки.
 |
Например, если имеется вариационный ряд (–3, –2, 2, 4, 5), то
имеет график, изображённый на рис.1.1.
Рис.1.1. Статистическая функция распределения выборки.
Функция имеет скачки, кратные 1/n, в точках значений выборки. При большом объёме выборки становится затруднительно строить точный график . Поэтому можно построить её приближённый график. Это делается следующим образом. Находятся точки графика для границ частичных интервалов группированной выборки и соседние точки графика соединяются прямолинейными отрезками. Образец такого графика приведён на рис.1.2.
 |
Рис.1.2. Статистическая функция распределения группированной выборки.
Гистограммой называется совокупность прямоугольников, основаниями которых служат частичные интервалы, а высоты равны соответствующим плотностям относительных частот. При этом площадь i –го прямоугольника равна
,
то есть она равна относительной частоте попадания элементов выборки в этот интервал.
Если середины верхних сторон прямоугольников соединить ломаной линией, то получается полигон. На рис.1.3. изображены образцы гистограммы и полигона.
 |
Рис. 1.3. Гистограмма и полигон группированной выборки.
Какую же информацию можно извлечь из статистической функции распределения, гистограммы и полигона? Пусть случайная величина X имеет функцию распределения Fx(x), то есть Fx(x) равна вероятности события X < x:
Fx(x) = P(X< x). (1.5)
Статистическая же функция распределения (1.4)равна уже относительной частоте того же события. В теории вероятностей известен так называемый закон больших чисел, в силу которого относительная частота любого события в серии из n независимых опытов сходится с вероятностью единица к вероятности этого события при бесконечном увеличении числа опытов. Следовательно, с вероятностью единица:
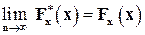. (1.6)
В нашем же случае, объём выборки n ограничен (хотя и может быть очень большим), поэтому может служить некоторым приближением неизвестной Fx(x):
Fx(X)» . (1.7)
Таким образом, полученная статистическая функция распределения является приближением исследуемой случайной величины X. И это приближение будет улучшаться с ростом объёма выборки и числа частичных интервалов.
Производная функции распределения случайной величины X называется её плотностью распределения вероятностей:
fx(x) = 
(1.8)
