Оценка средней величины имеет целью установить величину генеральной средней для изученной категории объектов. Требуемая для этой цели ошибка репрезентативности определяется по формуле:
(10.18)
Пример
При изучении шерстной продуктивности одной породы овец было взято из разных мест обитания породы у 100 взрослых овец 100 годовых настригов шерсти. Средний настриг у 100 овец оказался μ = 5,0 кг, стандартное отклонение для этой выборки s = 1,0. Ответственность исследования обычная, поэтому был принят первый порог вероятности безошибочных прогнозов b1 = 0,95.
Оценка среднего настрига для всей породы может быть проведена следующим образом:
n = 100; μ = 5,0; s = 1,0; n = 100 – 1 = 99; t = 2,0;
D = 2,0 × 0,1 =0,2;
μmax =5,0 + 0,2 = 5,2 (возможный максимум);
μmin = 5,0 – 0,2 = 4,8 (гарантированный минимум).
Выводы
1 Средний настриг шерсти по изученной выборке равен
μ ± 
= 5,0 ± 0,2, доверительные границы генеральной средней 4,8 – 5,2. По этим показателям можно провести сравнение результатов проведенного исследования с результатами других работ.
2 Планировать выход шерсти (n = 10000) на основе проведенного исследования следует исходя из гарантированного минимума генеральной средней μmin = 4,8 кг на одну голову, или 48 т шерсти от всех взрослых овец породы.
3 Работы по стрижке, обработке, перевозке и хранению шерсти следует планировать исходя из возможного максимума генеральной средней μmах = 5,2 кг с головы, или 52 т от всех овец изученной категории.
Пример
При изучении способности к обучению белых мышей для каждой из 40 особей определенного происхождения регистрировалось время прохождения лабиринта в поисках корма после пятой попытки В одном опыте были получены следующие сводные показатели:
n = 40, μ = 7,0 мин, s = 3,0 мин
Требовалось определить возможное время прохождения лабиринта в среднем для мышей всей изучаемой линии, что можно сделать следующим образом: n = 40, μ = 7,0, s = 3,0, n = 40 – 1 = 39, t = 2 (ответственность обычная: b = 0,95), 
= 3 / 
= 0,48; D = 2 × 0,48 = 0,96 ≈ 1,0, т.е не более 7,0 + 1,0 = 8,0; не менее 7,0 – 1,0 = 6,0.
Выводы
1 Среднее время для опытной группы
μ ±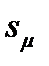 
= 7,0 ± 0,48 мин.
2 Доверительные границы генеральной средней
μ ± D = 6,0 – 8,0 мин.
3 Если встретится группа мышей со средним временем или меньше 6 мин. или больше 8 мин., возникнет предположение, что эта группа отличается от изученной по способности проходить лабиринт. Это предположение необходимо будет проверить методом определения достоверности разности.
Оценка средней разности
В некоторых исследованиях в качестве первичных данных берется разность двух измерений. Это может быть в случае, когда каждая особь выборки изучается в двух состояниях – или в разном возрасте, или при разных условиях жизни. В этих случаях индивидуальные и средние разности по своему знаку и величине могут характеризовать действие на изучаемый признак или возраста, или изменения условий жизни.
Характеристика действия определенных факторов по разности может быть произведена также и в экспериментах с аналогами, когда каждой особи в опытной группе соответствует строго определенная особь в контроле
Пример
При сортоиспытании пшеницы новый сорт А сравнивался со стандартным сортом В по разности урожаев, полученных на 20 парах параллельных делянок: di = Ai – Вi. В результате в качестве первичных материалов было получено 20 разностей, некоторые из них были положительными (A>В), некоторые – отрицательными (А<В).
Для всей выборки, состоящей из 20 разностей, были получены сводные выборочные показатели: n = 20, μ = + 1,0 ц/га, s = 2,5 ц/га. В этой выборке новый сорт оказался лучше стандартного: А – В= + 1,0; A>В.
Возник вопрос: а будет ли и весь новый сорт (а не только выборка из него) в аналогичных условиях лучше стандартного? Можно ли считать, что полученная средняя выборочная положительная разность d =+1,0 правильно отражает соответствующую генеральную разность между новым сортом и всем стандартным сортом? Будет ли эта генеральная разность 
тоже положительной? Этот вопрос можно решить путем оценки генерального значения средней разности на основе полученных сводных выборочных показателей.
Генеральный параметр изучаемой разности был оценен в форме доверительных границ с надежностью β2 = 0,99 (исследование имело большое экономическое значение) следующим образом:
n = 20, n = 20 – 1 = 19;
β2 = 0,99, t = 2,9, D = t×s = 2,9×0,56 = 1,6; n= 19.
не более + 1,0 + 1,6 = + 2,6 (A> В); не менее + 1,0 – 1,6 = –0,6.
Сортоиспытание выявило, что генеральная разность между сортами во всей их массе (а не только в изученной выборке) может находиться в доверительной зоне от +2,6 до –0,6 ц/га, в любой точке этой зоны – или в положительной, или в отрицательной, или в нулевой; если в положительной, значит весь новый сорт лучше стандартного (А > В), если в отрицательной, значит новый сорт хуже стандартного (А < В), если в нулевой, значит урожайность сортов одинакова (А = В, d = A – В = 0).
На основной вопрос: какой сорт лучше, А или В, – сортоиспытание дало ответ: или А лучше В, или А хуже В, или А не отличается от В.
