Оценка генеральных параметров по выборочным показателям имеет свои особенности.
Часть никогда не может полностью охарактеризовать все целое, поэтому характеристика генеральной совокупности на основе выборочного исследования всегда будет неточной, всегда будет иметь некоторую большую или меньшую ошибку.
Такие ошибки являются ошибками обобщения, ошибками, связанными с перенесением результатов, полученных при изучении выборки, на всю генеральную совокупность и называются ошибками репрезентативности.
Ошибки репрезентативности в оценке генеральных параметров нельзя путать с другими видами ошибок, которые могут появиться в биологических работах.
Вообще могут встретиться пять категорий ошибок в выборочных и сплошных исследованиях. Из них первые четыре не могу быть вскрыты при анализе уже полученного материала биометрическими методами.
Надо отбросить необоснованные надежды на то, что методические ошибки, ошибки точности, ошибки внимания и ошибки типичности, допущенные при сборе первичного материала, могут каким-то образом быть обезврежены или учтены последующим применением математических методов. Эта возможность имеется только по отношению к пятой категории ошибок – к ошибкам репрезентативности.
Краткое описание ошибок всякого исследования можно представить в следующем виде.
А) Ошибку, которые нельзя учесть статистическими методами, но избежать или свести их к минимуму можно хорошей организацией исследования.
1 Ошибки методические возникают при применении неправильной методики сбора и обработки материалов, при неточном проведении химических анализов, при невыравненности общих условий жизни для контрольной и опытной групп и т. п.
2 Ошибки точности – это пороки первичной регистрации фактов, измерение непроверенными, испорченными инструментами, расчеты с недостаточной, а также и с избыточной ненужной точностью.
3 Ошибки внимания – описки, просчеты, перепутывание материалов, опечатки.
4 Ошибки типичности (иногда их неправильно называют ошибками репрезентативности) возникают главным образом в начальных стадиях экспериментов и наблюдений. Это особенно опасный вид ошибок, происходящих оттого, что в выборку отбирается группа объектов, нетипичная для всей генеральной совокупности, и по такой выборке делаются прогнозы на всю генеральную совокупность, вследствие чего получается сильно искаженная характеристика всей массы объектов изучаемой категории.
Ошибки типичности могут быть допущены бессознательно, при непонимании того, что в выборку должны привлекаться объекты без учета у них величины изучаемого признака, в случайном порядке – рендомизированно.
Ошибки типичности могут быть причиной совершенно ложных генеральных выводов, если они применяются сознательно, при тенденциозном подборе первичных данных в соответствии с тем, что хочет получить во что бы то ни стало недобросовестный автор исследования. Такие ошибки не могут быть вскрыты или учтены статистикой; ликвидация их целиком лежит на совести авторов биологических исследований.
Б) Ошибки, учитываемые статистическими методами, но неустранимые при проведении любого биологического исследования.
Ошибки репрезентативности возникают всегда, когда требуется по части охарактеризовать целое. Это неизбежные ошибки, вытекающие из самой сущности выборочного исследования: вся генеральная совокупность может быть охарактеризована по одной своей части только с некоторой ошибкой, с определенной погрешностью. Ошибки репрезентативности не могут быть устранены при любой организации работ (за исключением перехода на сплошное изучение).
Законен вопрос: зачем проводить исследование, которое безнадежно обречено на получение ошибочных результатов? Ответ на этот вопрос содержится в особых свойствах этих ошибок.
Во–первых, ошибки репрезентативности можно свести к достаточно малой величине, к величине допустимой погрешности, практически приемлемой при оценке генеральных параметров в конкретных условиях. Делается это путем привлечения в выборку достаточного количества объектов.
Во–вторых, возможную величину ошибок репрезентативности можно определить на основе анализа выборочных данных и учесть при оценке генеральных параметров.
Математическая статистика дает способы определения ошибок репрезентативности (ошибок выборочных показателей) средней арифметической s, доли sр, разности двух выборочных показателей sd, коэффициента корреляции sr и др.
Понимание сущности ошибок репрезентативности предохранит от необоснованного их применения. Определять величину ошибок репрезентативности требуется только для выборочных показателей, так как генеральные параметры не имеют ошибок репрезентативности.
Предположим, две отары овец исследуются в порядке серийного отбора как выборки из двух различных генеральных совокупностей, например из двух пород, для характеристики этих пород. В этом случае расчет ошибок репрезентативности средних показателей совершенно необходим для получения правильных выводов и для правильного сравнения обеих генеральных совокупностей – пород по изучаемому признаку.
Если же исследуются не выборки, а генеральные совокупности, определять ошибки репрезентативности не нужно. Например, определяется, в отаре какого чабана получен больший настриг шерсти за год. Для этой цели, исследуются две отары и по каждой определяется требуемая средняя годовая величина настрига. В данном случае расчет ошибок репрезентативности не будет иметь ни теоретического, ни практического применения. Обе отары в этом случае являются генеральными совокупностями, сравниваемыми на основе сплошного исследования. Поэтому любой статистический показатель по этим стадам определяется без ошибок репрезентативности. Такие невыборочные показатели могут иметь все другие категории ошибок, не учитываемых математической статистикой, но ошибок репрезентативности они не имеют.
Определять величину ошибок репрезентативности следует только в тех случаях, когда организация исследования исключает все другие виды ошибок или когда все они сведены к минимуму. Например, изучается вес рыб, идущих косяком, в котором впереди – самки, за ними – молодь и сзади – самцы. Если в выборку попали рыбы главным образом из головной части косяка, то при определении среднего веса для всего косяка будет допущена ошибка типичности: в выборку попали особи только из одной части генеральной совокупности, отличающейся от остальных частей. Очевидно, что в данном случае расчет ошибок репрезентативности уже не поможет, так как отбор особей в выборку произведен неправильно.
Доверительные границы
Определять величину ошибок репрезентативности необходимо для того, чтобы выборочные показатели использовать еще и для нахождения возможных значений генеральных параметров. Этот процесс называется оценкой генеральных параметров.
Оценка генеральных параметров не может быть выражена одним числом: это точное значение параметра остается неизвестным. Но математические методы дают возможность определить, в каких пределах может находиться значение генерального параметра. Практически такая приближенная оценка имеет часто большое значение, например, в метеорологии при прогнозе температуры: «завтра ожидается в Гомеле 15 – 17 градусов тепла».
Оценка генеральных параметров по выборочным данным производится особым способом в форме не одного, а двух значений – минимального и максимального. Эти крайние значения, в пределах которых может находиться искомая величина генерального параметра, называются доверительными границами. Доверительные границы любого генерального параметра определяются по следующему общему правилу.
Генеральный параметр может отличаться от найденного выборочного показателя не более, чем на величину возможной погрешности, определяемой по выборочным данным. Это правило выражается следующими формулами:
или
или
где:
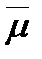– генеральный параметр;
– выборочный показатель;
– максимальная доверительная граница, или возможный максимум;
– минимальная доверительная граница, или гарантированный минимум;
– возможная максимальная абсолютная погрешность при прогнозе генерального параметра;
t – критерий надежности, или показатель вероятности того, что величина генерального параметра действительно будет находиться внутри найденных доверительных границ;
– показатель точности оценки генерального параметра, или ошибка репрезентативности выборочного показателя.
Для предварительной иллюстрации значения всех элементов определения доверительных границ имеет смысл рассмотреть следующий пример, в котором величины t и 
берутся уже готовыми.
Пример
Промеры шкурок 100 добытых подряд зайцев и последующий расчет дали следующие выборочные показатели размеров шкурок: n = 100, μ = 800 см2, s = 80 см2. Кроме того, были установлены критерий надежности t = 2 (что соответствует первому порогу вероятности безошибочных прогнозов) и стандартная ошибка (показатель точности):
На основе этих данных доверительные границы генеральной средней размера шкурок определятся следующим образом:
;
;
;
не более 800+16 = 816; не менее 800–16 = 784.
Таким образом, искомая средняя размеров заячьих шкурок может быть не более 816 и не менее 784. Эти доверительные границы имеют в данном случае определенный практический смысл.
Планирование общего выхода шкурок при годовом промысле зайцев лучше вести на основе гарантированного минимума. Например, если предполагается добыть 10000 зайцев, то лучше ожидать, что общая площадь полученных шкурок будет:
784 × 10000 = 7840000 см2.
Все же подсобные мероприятия (расходы по организации промысла, средства доставки, выделка шкурок, складские помещения) лучше планировать из расчета возможного максимума:
816 × 10000 = 8160 000 см2.
Вопросы для самоконтроля
1 Что такое совокупность? Примеры различных совокупностей.
2 Чем отличается выборочная совокупность от генеральной?
3 Что называется генеральными параметрами?
4 Перечислить и охарактеризовать основные способы отбора объектов в выборку.
5 Что называется выборочными показателями?
6 Дайте определение репрезентативности.
7 Если репрезентативность выборочных данных может быть выражена в достаточной или в недостаточной степени, то, как можно охарактеризовать оценки генеральных параметров?
8 Перечислите основные категории ошибок в выборочных и сплошных исследованиях.
9 В каком случае ошибки репрезентативности могут быть устранены.
10 На какую величину генеральный параметр может отличаться от найденного выборочного показателя?
11 Дайте определение и формализацию максимальной и минимальной доверительной границы.
12 Дайте определение критерия надежности?
ТЕМА 10 Оценка генеральных параметров
10.1 Общий порядок оценки
10.2 Критерий достоверности разности
10.3 Репрезентативность при изучении качественных признаков
10.4 Достоверность разности долей
Общий порядок оценки
Три величины, необходимые для оценки генерального параметра, – выборочный показатель (
), критерий надежности (t) и показатель точности (
) – определяются следующим образом.
Выборочный показатель () рассчитывается по выборочным материалам способом, изложенным при описании этого показателя.
Критерий надежности (t) определяется заранее, при планировании исследования, исходя из представления о большей или меньшей ответственности возможных результатов работы. Критерий надежности – это показатель вероятности безошибочных прогнозов.
Практика биологических работ выработала три основных порога вероятности безошибочных прогнозов: при обычной ответственности
b1 = 0,95, при повышенной ответственности b2 = 0,99 и при высокой ответственности b3 = 0,999.
Критерий надежности (t) связан с этими тремя порогами вероятности безошибочных прогнозов (b) при достаточно больших выборках так, как это показано в таблице 10.1.
Таблица 10.1 – Три порога надежности (вероятности безошибочных прогнозов)
| Порог | Применение | Вероятность безошибочных прогнозов | Критерий надежности | Объем выборок |
| Обычные требования надежности | β1 = 0,95 | t1= 1,960 | n1 > 30 | |
| Повышенные требования | β2 =0,99 | t2=2,576 | n2 > 100 | |
| Высокие требования надежности | β3 = 0,999 | t3 = 3,291 | n3 > 200 |
Для выборок, объем которых меньше указанного в таблице 10.1, и вообще для выборок любого объема значение t определяется по таблице критериев Стьюдента, в которых критерии надежности приводятся для любого объема выборок в зависимости от числа степеней свободы данного показателя, для каждого из трех порогов вероятности безошибочных прогнозов. Таблицы критериев Стьюдента приведены в учебниках по математической статистике.
При отсутствии таблицы критериев Стьюдента стандартные значения критерия надежности можно определить с достаточным приближением по формуле:
; (10.1)
tst – стандартное значение критерия при числе степеней свободы n;
– критерий надежности для достаточно больших выборок
(t1 = 2.0; t2 = 2,6; t3 = 3,3);
Для обычных требований надежности (b = 0.95) эта формула приобретает более простой вид:
; (10.2)
Показатель точности или ошибка репрезентативности выборочного показателя определяется на основе выборочных данных по формулам математической статистики.
Ошибка средней арифметической:
; (10.3)
Ошибка среднего квадратического отклонения:
; (10.4)
Ошибка коэффициента вариации:
; (10.5)
Ошибка разности средних:
а) при некоррелированных выборках:
; (10.6)
б) при коррелированных выборках:
; (10.7)
(r – коэффициент корреляции)
Ошибка показателя асимметрии:
; (10.8)
Ошибка показателя эксцесса:
; (10.9)
Средняя ошибка суммы нескольких средних:
; (10.10)
Средняя ошибка произведения двух выборочных средних:
; (10.11)
Средняя ошибка частного двух выборочных средних:
; (10.12)
Средняя ошибка разности выборочных средних двух независимых распределений.
При n1 = n2:
; (10.13)
При n1 ≠ n2:
; (10.14)
Объединенная дисперсия двух выборок:
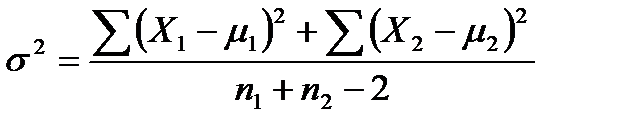; (10.15)
Средняя ошибка разности в парных опытах:
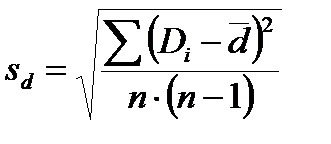; (10.16)
Di – разности между вариантами сопряженных рядов X1 и X2;
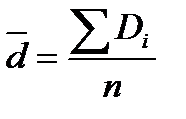; (10.17)
n – общее число парных наблюдений.
Итак, для того чтобы оценить генеральный параметр для количественных признаков в форме доверительных границ необходимо:
1 Проверить на нормальность распределения исходных данных.
2 Установить число степеней свободы по правилам, приведенным при описании оценки каждого параметра.
3 Установить, исходя из ответственности исследования (таблица 10.1), порог вероятности безошибочных прогнозов
(β1 = 0,95, β2= 0,99, β3= 0,999).
4 В соответствии с числом степеней свободы найти значение критерия надежности t по таблице стандартных значений критерия Стьюдента. При отсутствии таблицы показатель надежности для данного исследования можно приближенно определить по приведенным формулам. Если объем выборки превышает нижние пределы больших выборок (n > 30, n > 100, n > 200), то показатели надежности берутся постоянные для каждого порога вероятности:
t1 = 2.0; t2 = 2.6; t3 = 3,3.
5 Рассчитать ошибку выборочного показателя по формулам, приведенным выше и указанным при описании оценки каждого параметра.
6 Определить возможную погрешность оценки генерального параметра, помножив критерий надежности на ошибку репрезентативности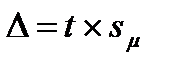 
.
7 Установить доверительные границы генерального параметра; возможный максимум: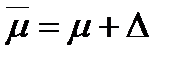 
и гарантированный минимум: 
.
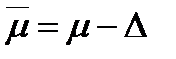