Всякая электрическая цепь, по которой протекает переменный ток, может излучать электромагнитные волны. Эти волны, распространяясь в диэлектрике, окружающем источник, переносят определенную энергию. Излучаемая энергия зависит от амплитуды и частоты тока, от конфигурации цепи и от свойств диэлектрика, окружающего источник.
Для промышленной частоты f=50Гц излучаемая мощность мала. Мощность излучения необходимо учитывать, начиная с частоты f=0.1МГц и выше (радиочастоты).
Рассмотрим электрическую цепь синусоидального тока, изображенную на рис. 4.1, а.
Пусть при действии ЭДС е в контуре 1, ток в контуре 2 равен i, а напряжение на емкости равно uc. Тогда энергия магнитного и электрического полей будут определяться выражениями
Энергия пульсирует с частотой, равной удвоенной частоте тока. Часть этой энергии распространяется со скоростью u=1/Öem в окружающем цепь диэлектрике (с параметрами e и m).
Контур 2 можно видоизменить так, как показано на рис. 4.1,б и рис.4.1,в. Следовательно, прямолинейный провод длиной l, по которому протекает переменный ток, может излучать электромагнитные волны. Такой провод представляет собой простейшую антенну. Часто простейшую антенну, по которой протекает синусоидальный ток, называют элементарным вибратором.
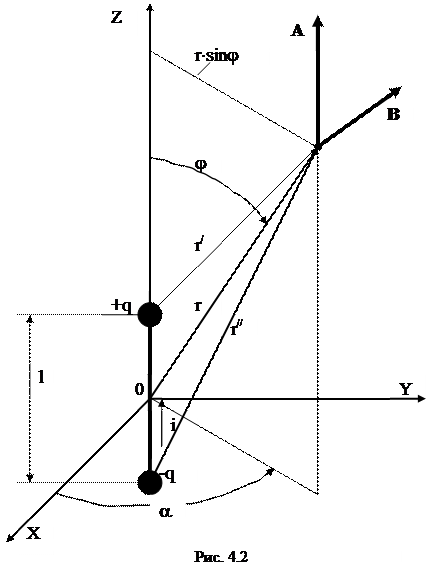
Электромагнитное поле, излучаемое вибратором, полностью аналогично полю, создаваемому излучающим диполем. Под излучающим диполем понимают отрезок линейного провода с сосредоточенными на концах его емкостями в виде шаров (рис. 4.2).
Рассмотрим поле такого излучающего диполя. При этом будем полагать, что длина диполя l много меньше длины волны c. Предположим также, что вся емкость такого вибратора есть емкость между сферами и что соединительный проводник обладает только индуктивностью.
 |
При возникновении колебаний в данной системе переменный ток в каждый момент времени имеет одно и то же значение вдоль всего проводника.
Такой вибратор на расстояниях r от него, намного превышающих l, можно рассматривать как диполь с переменным электрическим моментом. Поместим в начале координат и направим его ось по оси 0Z (рис. 4.2), тогда
Если r>>l, то можно записать
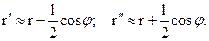
Разложим функцию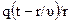 
в ряд Тейлора и, ограничиваясь двумя первыми членами разложения (с учетом малости (lcosj)/2), получим:
Следовательно,
.
Опуская обозначения аргументов у функций q и i, а также учитывая, что
получим выражения для определения составляющих магнитной индукции
Так как Вх/Ву=-у/х, то вектор магнитной индукции В направлен по касательной к окружности, лежащей в плоскости, перпендикулярной оси 0Z и имеющей центр на этой оси. Следовательно, вектор В имеет единственную составляющую Вa, равную
(4.15)
Используя выражение (4.11), а также учитывая, что
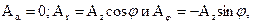
определим составляющие напряженности электрического поля Еa, Еj, Еz в сферической системе координат. Заметим при этом, что скалярный потенциал U можно представить в виде
и тогда
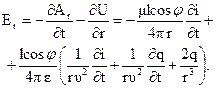
Так как 1/(eu2) = m, то первое слагаемое и первый член в скобках сокращаются, и выражение для радиальной составляющей напряженности электрического поля можно переписать в следующем виде:
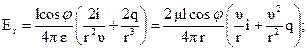(4.16)
или
. (4.17)
Наконец, с учетом того, что Аa и U не зависят от a, Еa=0.
Таким образом, можно сделать вывод, что в электромагнитной волне, излучаемой диполем также как в плоской волне, напряженность электрического поля перпендикулярна вектору магнитной индукции.
Рассмотрим случай, когда по проводнику протекает синусоидальный ток
Здесь w - угловая частота колебаний (w=2pf=2p/T).
Замечая, что
получаем
С учетом последних выражений перепишем формулы (4.15) ¸ (4.17)
(4.18)
(4.19)
(4.20)
Иногда удобнее использовать не мгновенные значения векторов электромагнитного поля, а их комплексные изображения, поэтому перепишем последние уравнения после некоторых преобразований в комплексной форме
Здесь j – мнимая единица; b=2p¤l.
Формулы (4.18) ¸ (4.20) (а также последние выражения) позволяют сделать вывод о том, что в любой точке пространства напряженность магнитного поля имеет две составляющие, одна из которых убывает обратно пропорционально квадрату радиуса r и изменяется во времени по закону синуса, а другая убывает обратно пропорционально первой степени радиуса и изменяется во времени по закону косинуса. Составляющая напряженности электрического поля Еj является суммой трех слагаемых, изменяющихся обратно пропорционально соответственно первой, второй и третьей степени расстояния r. Составляющая Еr состоит из двух слагаемых, изменяющихся обратно пропорционально r2 и r3.
При исследовании электромагнитного поля, излучаемого антенной, принято все пространство вокруг антенны подразделять на ближнюю, среднюю (или промежуточную) и дальнюю зоны.
Ближняя зона ограничивается радиусом, величина которого много меньше длины волны (r<<l). Дальняя зона расположена от антенны на расстоянии, намного превышающем длину волны (r>>l). В средней зоне расстояние от антенны до любой точки соизмеримо с длиной волны.
В ближней зоне преобладают составляющая электрического поля, меняющаяся пропорционально 1/r3, и составляющая магнитного поля, пропорциональная 1/r2. В соответствии с этим, для ближней зоны можно оставить только последние члены в выражениях для Нa, Еj и Еr
или в комплексной форме
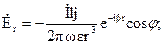
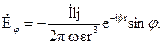
Магнитная индукция (Вa=mНa) элементарного вибратора в ближней зоне определяется так же, как и в случае постоянного тока (закон Био - Савара). Фаза В совпадает с фазой тока i. Магнитное поле токов смещения этой формулой не учитывается.
Приближенные формулы для Еr и Еj совпадают с формулами поля для статического диполя.
Вектор Пойнтинга (4.5) имеет две составляющие Пr и Пj и среднее значение каждой из них за период равно нулю. Таким образом, вектор Пойнтинга в ближней зоне определяет реактивную (связанную) часть мощности (векторы напряженности электрического и магнитного поля сдвинуты по фазе на 90°).
В ближней зоне энергия излучения не учитывается.
Границы ближней зоны зависят от частоты: чем выше частота, тем ближе граница зоны к источнику.
Для частоты f=50Гц длина волны l=6000 км и поэтому в любом удалении от источника зону можно считать ближней. Для радиочастот, которые могут достигать значений 1010Гц и выше, длина волны измеряется в сантиметрах, поэтому все пространство вокруг источника может рассматриваться как дальняя зона.
Ближняя зона носит так же название квазистационарности, так как для мгновенных значений векторов переменного поля применимы с достаточной точностью законы постоянных во времени полей.
В дальней зоне (зоне излучения) преобладают составляющие Е и Н, меняющиеся пропорционально 1/r и совпадающие по фазе. Поэтому в выражениях для Нa и Еj можно пренебречь всеми членами, кроме первых. Составляющей Еr можно пренебречь полностью, так как оба ее члена весьма малы по сравнению с первым членом составляющей Еj.
В комплексной форме эти выражения имеют следующий вид:
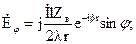(4.21)
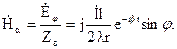(4.22)
Волна, имеющая такой характер, называется сферической, она имеет структуру поля волны типа ТЕМ (буквами ТЕМ обозначают поперечные волны, то есть такие волны, у которых в направлении распространения отсутствуют составляющие векторов напряженностей электрического и магнитного полей).
Таким образом, в сферической волне, как и в плоской, энергия электрического поля равна энергии магнитного поля (eЕ2=mН2).
Если провести сферу радиусом r, то во всех точках этой сферы (такая сфера носит название эквифазной поверхности) напряженность магнитного поля Н имеет одну и ту же фазу колебания в какой-то конкретный момент времени (фаза колебания определяется аргументом косинуса). Амплитуда Н для всех точек сферы (r=const) различна, она зависит от угла j. На «полюсах» при j=p амплитуда колебания для любого момента времени равна нулю. Амплитуда колебания максимальна на «экваторе» сферы при j=p/2. По фазе Н и Е совпадают и, следовательно, определяют активную мощность. Таким образом, они характеризуют свободно распространяющуюся энергию.
Как видно из (4.21) и (4.22), элементарный электрический вибратор обладает направленными свойствами. Диаграмму зависимости модуля Е или Н в дальней зоне принято называть диаграммой направленности. Максимальное излучение (максимальная напряженность поля), как было отмечено выше, получается в экваториальной плоскости, т. е. в плоскости, перпендикулярной оси вибратора и проходящей через его середину. На рис.4.3 приведена диаграмма направленности в меридиональной плоскости элементарного вибратора. Диаграмма построена в полярной системе координат и характеризует зависимость Е и Н от j в дальней зоне. Диаграмма имеет форму восьмерки.
Мощность, излучаемая элементарным электрическим вибратором, определяется путем интегрирования вектора Пойнтинга по эквифазной поверхности (радиус поверхности выбирается достаточно большим, чтобы она находилась в дальней зоне).
Вектор Пойнтинга
в любой момент времени направлен по радиусу в сторону от диполя.
Среднее за период Т значение вектора Пойнтинга
где I – действующее значение тока.
Проходящая через элементарную площадку ds сферы средняя мощность
Интегрируя последнее выражение, находим излучаемую вибратором среднюю за период мощность
(4.23)
Коэффициент при I2/2 имеет размерность сопротивления, его называют сопротивлением излучения
. (4.24)
В свободном пространстве и в воздухе ZВ=120p и
(4.25)
Таким образом, чем больше сопротивление излучения RS, тем больше излученная мощность при том же токе I. Из анализа формул (4.24) и (4.25) видно, что сопротивление излучения пропорционально квадрату длины излучателя и, что особенно важно, обратно пропорционально квадрату длины волны l. Так как длина волны l=u/f, то излученная мощность пропорциональна квадрату частоты. Если частота мала, например всего 50 Гц, то излучения практически нет. При радиочастоте излучение значительно. Например, при частоте 50 МГц излучение больше, чем при частоте 50 Гц, в 1012 раз.
Выше было рассмотрено электромагнитное поле, излучаемое элементарным электрическим вибратором. Для решения некоторых задач по определению электромагнитного поля удобнее пользоваться понятием элементарного магнитного вибратора.
Таким вибратором называют элемент линейного магнитного тока Iм или линейный элемент, на поверхности которого имеется ненулевая тангенциальная составляющая вектора напряженности электрического поля Е, перпендикулярная оси элемента, а тангенциальная составляющая вектора напряженности магнитного поля Н равна нулю.
Не останавливаясь здесь на математических выкладках, приведем в комплексной форме формулы для определения составляющих напряженности электрического и магнитного полей в сферической системе координат
;
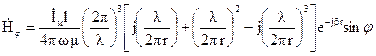Из приведенных формул видно, что поле элементарного магнитного вибратора имеет радиальную составляющую вектора напряженности магнитного поля Нr, которая совпадает с направлением распространения волны. В этом смысле структура электромагнитного поля вокруг магнитного вибратора подобна структуре волн типа Н.
В ближней зоне преобладают составляющая электрического поля, меняющаяся пропорционально 1/r2, и составляющие магнитного поля, пропорциональные 1/r3. В соответствии с этим, для ближней зоны можно оставить только последние члены в выражениях для Еa, Нj и Нr
В дальней зоне, где можно пренебречь составляющими, пропорциональными 1/r2 и 1/r3, напряженности полей элементарного магнитного вибратора равны:
(4.26)
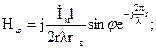(4.27)
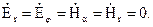
Приведенная структура формул показывает, что поле элементарного магнитного вибратора имеет структуру, идентичную структуре поля элементарного электрического вибратора, только Е и Н взаимно меняются местами.
Для выяснения физической модели элементарного магнитного вибратора и такого понятия, как магнитный ток Iм, рассмотрим поле излучения кругового конура с током Ip или рамочной антенны (рис. 4.4). Не останавливаясь здесь на математических выкладках, приведем формулы для определения напряженности электрического и магнитного полей в произвольной точке Р, находящейся в дальней зоне, созданных рамкой с током (которая и называется вибратором).
Комплексные амплитуды напряженности электрического и магнитного полей можно представить следующим образом:
(4.28)
(4.29)
Здесь Sp – площадь, ограниченная контуром рамки.
Рассмотрим теперь связь между реальным током Iр, который протекает в рамке и магнитным током Iм, которого на самом деле в природе не существует. Введение в рассмотрение этого фиктивного тока целесообразно только потому, что с его помощью сложные поля излучения можно характеризовать, как это показано выше, формулами, аналогичными выражениям, представляющим известные поля электрических диполей. Магнитный ток можно физически реализовать контуром тока с изменяющимся во времени магнитным моментом Мм, который определяется через ток при помощи следующего соотношения:
Магнитный момент, также как момент электрического диполя можно рассчитать через фиктивные электрические заряды Qm, если ввести в рассмотрение магнитный диполь (рис. 4.5).
В этом случае, магнитный момент будет равен
Если заряды изменяются во времени, то так же, как в электрическом диполе будет протекать электрический ток, в магнитном диполе будет протекать магнитный ток, пропорциональный скорости изменения зарядов во времени
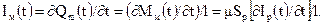
Если ток в рамке изменяется по гармоническому закону, то последнее выражение можно представить в комплексной форме
Таким образом, магнитный ток, это фиктивный ток, который течет между фиктивными зарядами и направлен перпендикулярно плоскости рамки с реальным током.
Если из последней формулы определить ток Iр и подставить его значение в выражения (4.28) и (4.29), то после небольших преобразований, мы придем к формулам (4.26) и (4.27).
Используя выражения (4.28) и (4.29), можно найти мощность излучения элементарного магнитного вибратора, выполненного в виде рамки
где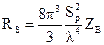 
- сопротивление излучения рамки.
Одним из возможных вариантов практического осуществления магнитного вибратора является также щелевой излучатель (щелевая антенна). Элементарный щелевой излучатель представляет собой тонкий металлический лист с высокой проводимостью, в котором прорезана щель, длина которой l много меньше длины волны (l<<l) и значительно больше ширины щели a (l>>a). Такая щель может быть возбуждена путем подведения к ее кромкам ЭДС (рис. 4.6) (или если эта щель прорезана на поверхности резонатора таким образом, что она разрезает токи проводимости).
Предположим, что проводимость листа равна бесконечности и что вдоль длины щели напряженность электрического поля одинакова по величине и фазе и равна Е0. Последнее может быть достигнуто практически путем выполнения щели аналогично диполю Герца (рис. 4.7) или же если щель представляет собой элемент щелевого вибратора конечных размеров.
Щель характерна тем, что на ее поверхности имеется тангенциальное электрическое поле и отсутствует тангенциальное магнитное поле. Таким образом, на поверхности щели создаются условия, характерные для элементарного магнитного вибратора. Поэтому напряженность полей, создаваемых элементарным щелевым вибратором в каждой точке пространства, выражается соответствующими формулами для магнитного вибратора.
В частности, составляющие напряженности поля в дальней зоне выражаются формулами (4.26) и (4.27), в которых под Iм следует подразумевать по аналогии с элементарным магнитным вибратором величину
где L – периметр, равный 2а (а – ширина щели).
Поэтому
(4.30)
(4.31)
где l – длина щели; j - угол между лучом, проведенным в точку наблюдения N, и осью щели (рис 4.8).
Формулы (4.30) и (4.31) получены в предположении, что напряженность поля поперек щели одинакова (что не всегда может соблюдаться). При неодинаковом значении напряженности Е0 поперек щели в формулах (4.30) и (4.31) следует заменить произведение Е0а интегралом 
. В некоторых случаях, более удобно выразить поле излучения щелевого вибратора через напряжение U между кромками щели, которое можно определить с помощью следующей формулы:
(или U=E0a при равномерной напряженности поля между кромками).
Подставляя в (4.30) и (4.31) U вместо Е0а, получаем:
(4.32)
.
Из сопоставления (4.42) с формулой (4.29) для напряженности поля элементарного электрического вибратора видно, что элементарные электрический и щелевой вибраторы одинаковой длины создают одну и ту же напряженность электрического поля, если U=0.5(ZвI), где I – ток в электрическом вибраторе. Диаграмма направленности элементарного щелевого вибратора такая же, как элементарного электрического вибратора, и определяется множителем sinj.
По аналогии с электрическим вибратором вводят понятие о проводимости излучения GS щелевого вибратора, определив ее из соотношения
. (4.33)
Найдем выражение для GS элементарного щелевого вибратора. Пусть имеем элементарные электрический и щелевой вибраторы одинаковой длины. Излучаемая электрическим вибратором мощность определяется выражением (4.23), которое с учетом формулы (4.24) можно переписать в следующем виде:
а мощность, излучаемая щелевым вибратором, определяется формулой (4.33). Предположим, что оба вибратора излучают одинаковую мощность, тогда
(4.34)
Для того чтобы мощности были одинаковыми, достаточно, чтобы оба вибратора создавали одинаковую напряженность поля в дальней зоне в направлении максимального излучения. Для этого, как было показано выше, должно выполняться соотношение U=0.5(ZвI). Подставляя значение этого напряжения в выражение (4.34), получаем
(4.35)
В свободном пространстве, где ZВ=120p,
(4.36)
