Основные определения
Магнитным полем называют одну из двух сторон электромагнитного поля, обусловленную движущимися заряженными частицами и изменением электрического поля, оказывающую силовое воздействие на движущиеся заряженные частицы и выявляемую по силовому воздействию, направленному нормально к направлению движения этих частиц и пропорциональному их скорости.
Основной физической величиной, характеризующей магнитное поле, является магнитная индукция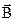 
.
Магнитная индукция – величина векторная. Единицей измерения магнитной индукции является тесла (Тл).
Численно магнитную индукцию можно определить по механической силе f2, действующей на один заряд q, движущийся со скоростью V
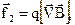
где 
- векторное произведение векторов скорости и магнитной индукции.
Если выбрать такое направление скорости 
, чтобы оно было перпендикулярно вектору магнитной индукции 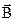, то величина скорости f2 будет наибольшей (f2max) и
Принято также магнитную индукцию 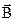определять по силовому воздействию на отрезок проводника длиной l, по которому протекает постоянный электрический ток I. Так, если проводник поместить в магнитное поле таким образом, чтобы он был перпендикулярен вектору магнитной индукции 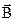, то
Магнитное поле, кроме магнитной индукции, характеризуется также намагниченностью вещества 
и напряженностью магнитного поля 
. Эти величины связаны следующим соотношением:
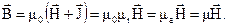
Здесь m0 – магнитная постоянная; mr – относительная магнитная проницаемость; mа и m - абсолютная магнитная проницаемость.
Единицей магнитной постоянной является генри на метр (Гн/м). Магнитная постоянная m0 имеет значение, равное 4p×10-7 Гн/м.
Единицей напряженности магнитного поля является ампер на метр (А/м).
Для изотропного вещества
,
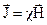где c - магнитная восприимчивость.
В частном случае для пустоты 
и 
Магнитный поток и его непрерывность
Поток вектора магнитной индукции сквозь некоторую поверхность s называют кратко магнитным потоком сквозь эту поверхность и обозначают через Ф
(3.1)
Магнитный поток измеряется в веберах (Вб).
Магнитный поток сквозь любую замкнутую поверхность s равен нулю (принцип непрерывности магнитного потока)
В дифференциальной форме принцип непрерывности магнитного потока имеет следующий вид:
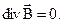(3.2)
Закон полного тока
При анализе магнитных полей важное значение имеет закон полного тока, который в интегральной форме имеет вид:
(3.3)
и гласит о том, что линейный интеграл по замкнутому контуру l от напряженности магнитного поля равен полному току, протекающему сквозь сечение, ограниченное этим контуром.
Под полным током понимают алгебраическую сумму токов проводимости, переноса и смещения.
В дифференциальной форме закон полного тока можно записать следующим образом:
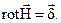(3.4)
