Загальна схема динамічної ідентифікації параметрів моделі.
На динамічних об’єктах проводяться активні та пасивні експерименти. Активні передбачають подачу на вхід об’єкта деякого збурюючого сигналу. Пасивні є результатом спостережень за об’єктом без втручання в хід технологічного процесу.
Розглянемо спочатку методи визначення параметрів об’єктаза результатами пасивних експериментів. У даному випадку загальна схема динамічної ідентифікації така:
Згідно загальної схеми ідентифікації вхідний сигнал Х подається на об’єкт Ф, а також на деякий ідентифікатор φ. В якості ідентифікатора виступає модель об’єкта(пристрій, програма). Задачею ідентифікатора є таке настроювання параметрів об’єкта, щоб вихідні сигнали Y та Y* відрізнялися найменшим чином. При цьому вихідний сигнал Y подається на ідентифікатор для порівняння із сигналом Y*.
Для знах. параметрів об’єкта вводиться ф-я нев’язки.
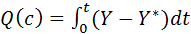– функція нев’язки.
Y*=Y*(X,Y,C)
t=NΔt
Δt – тривалість спостереження за об’єктом; N – к-сть спостережень.
Отже, знах. параметрів об’єкта С(С1,С2,…,Сn) згідно заг. схеми ідентифікації проводиться в дискретні моменти часу. Крім того для динамічних об’єктів вводяться початкові або крайові умови. Такі умови впливають на функціональний зв’язок параметрів моделі, а тому використовуються для керування ходом експерименту.
Ідентифікація моделі динамічногго об’єкта.
Динамічний об’єкт відрізняється від статичного тим, що його стан Yi визначається не тільки значеннями вхідних сигналів Xi, але і станом об’єкта в попередній момент часу Yi-1. Цу так звана “пам’ять” об’єкта, що робить його інерційним.
Дискретна загальна модель динамічного об’єкта на стадії ідентифікації:
Yi=F(Yi-1,Xi,C)
Задача ідентифікації полягає в тому, щоб визначити параметри С, при яких ф-я нев’язки буде мінімальною. При цьому визначення параметрів відбувається в дискретні моменти часу. Ф-я нев’язки в даному випадку така:
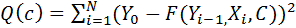
Yi,Yi-1,Xi – експериментальні значення вихідного та вхідного сигналів.
Yi-1 – значення вихідного сигналу в попередній по відношенню до Yi момент часу.
Ідентифікація з використання моделей Вольтера.
Нехай маємо деякий одномірний нелінійний об’єкт з одним вхідним і одним вихідним сигналом. Розглянемо випадок коли сигнал і оператор об’єкта не залежать від часу. Тобто маємо стаціонарний випадок, коли вихідний сигнал Y(t) не залежить від часу, але залежить від моменту дії вхідного сигналу X(t) і даного моменту. За таких умов зв’язок між вхідним і вихідним сигналом може бути заданий рядом Вольтера:
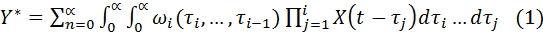
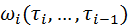– вагова ф-я, яку необхідно ідентифікувати.
Для практичних розрахунків y (1) обмежується відрізком ряду i=2. Тоді (1) матиме вигляд:
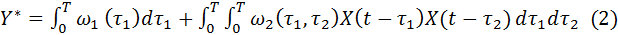
Де вагові ф-ї ω1 і ω2 шукаються у вигляді:
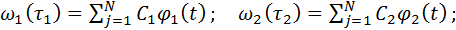
φ1(t) і φ2(t) лінійно незалежні ф-ї, які виражаються із умови:
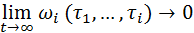
C1 і C2 шукаються за МНК із ф-ї нев’язки, яка у даному випадку має вигляд:
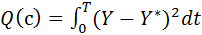
У даному випадку ідентифікація за рядами Вольтера співпадає із загальною схемою ідентифікації, але структура моделі безпосередньо не задана, а формується з допомогою рядів Вольтера.
