Потоковая сеть представляет собой ориентированный граф, удовлетворяющий некоторым специальным условиям и обладающий некоторыми дополнительными (по отношению к произ-вольным графам) параметрами. Необходимые понятия и определения теории графов даны в предыдущей главе 6; будем пользоваться введёнными там понятиями без дополнительных разъ-яснений, останавливаясь лишь на новых (ранее не определённых) понятиях и терминах.
При определении сети в базовом простейшем случае рассматривают ориентированные связные графы, обладающие следующими специальными свойствами:
1) существует ровно одна вершина, в которую не входит ни одна дуга (эта вершина называется источником);
2) существует ровно одна вершина, из которой не выходит ни одна дуга (эта вершина называет-ся стоком);
3) ни одна дуга не является петлёй.
Потоковой сетью) называется граф указанного типа, у которого каждой дуге vj (j = 1, 2,..., m) сопоставлено положительное число сj (j = 1, 2,..., m), называемое пропускной способнос-тью дуги vj. Пример потоковой сети приведен на рис.1. Пропускные способности проставлены в кружках около дуг.
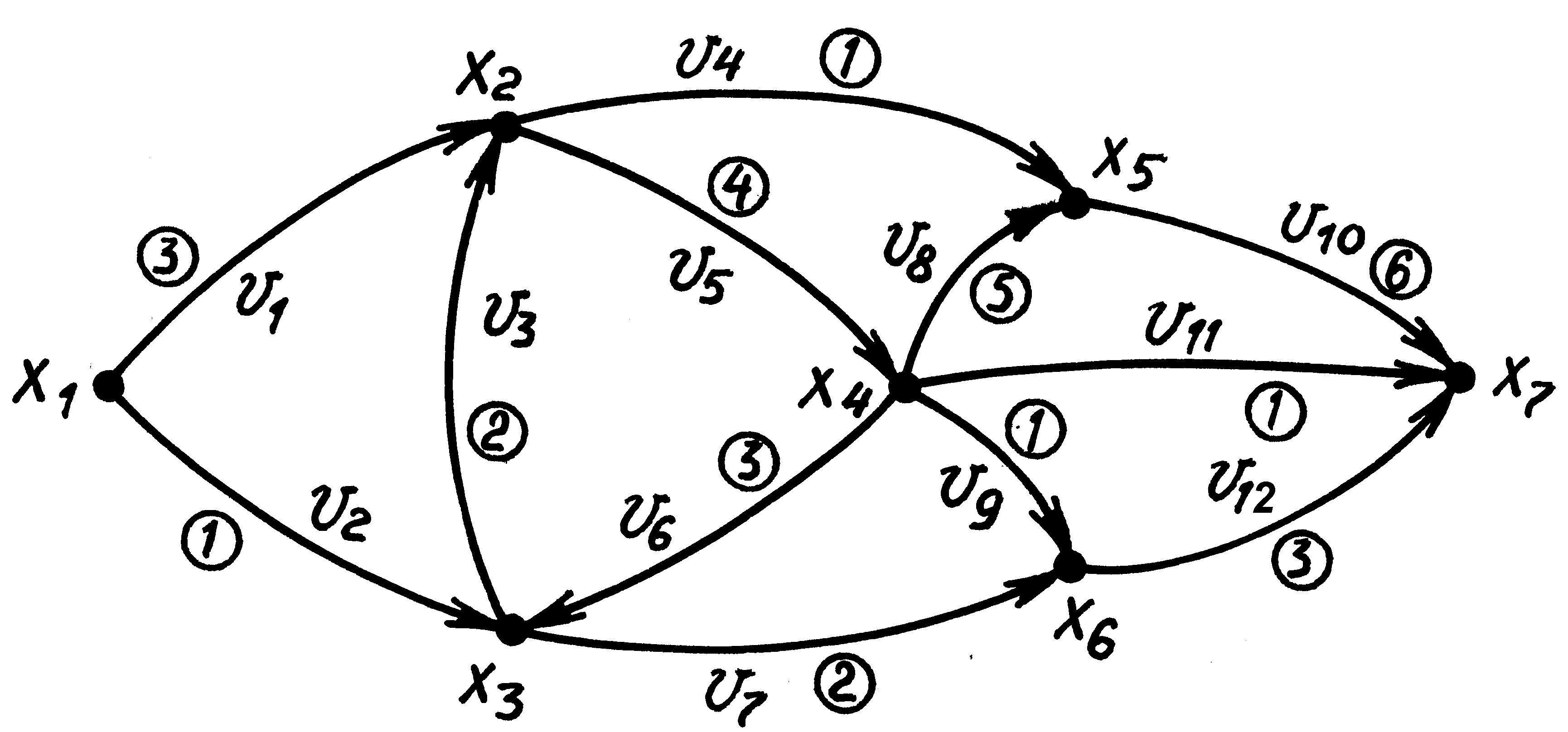
Рис.1
Таким образом, потоковая сеть - это ориентированный граф, в котором заданы пропуск-
ные способности дуг. В дальнейшем будем удобно занумеровать вершины графа так, чтобы вершина с минимальным номером (x 1) являлась источником, а вершина с максимальным номе-ром (xn) являлась стоком сети. Потоковую сеть будем обозначать через S.
Введем обозначения:
- множество номеров всех дуг, входящих в вершину xi;
- множество номеров всех дуг, выходящих из вершины xi.
Пример 1. В сети, показанной на рис.1:
n = 7, m = 12,
= {1,2},
= {1,3}, 
= {4,5}, 
= {2,6}, 
= {3,7}, 
= {5}, 
= {6,8,9,11},
= {4,8}, 
= {10}, 
= {7,9}, 
= {12},
= {10,11,12},
= 
= Æ (по определению сети, так как у источника нет входящих, а у стока - выходящих дуг);
с 1=3, с 2=1, с 3=2, с 4=1, с 5=4, с 6=3, с 7=2, с 8=5, с 9=1, с 10=6, с 11=1, с 12=3 ■
Потоком в сети называется вектор u = (u 1, u 2,..., um)
удовлетворяющий условиям
0 ≤ uj ≤ сj (j = 1, 2,..., m), (1)
(i = 2, 3,..., n -1). (2)
Компонента uj вектора u = (u 1, u 2,..., um) называется потоком по дуге vj (j = 1, 2,..., m). Таким образом, условие (1) означает, что поток по любой дуге - неотрицательное число, не превос-ходящее пропускной способности этой дуги. Условие (2) означает, что сумма потоков по всем дугам, входящих в вершину, равна сумме потоков по всем дугам, выходящих из этой же верши-ны (кроме источника и стока).
Содержательно поток описывает распределение по дугам сети некоторого продукта, до-ставляемого из источника в сток. При этом поток uj по дуге vj - это количество продукта, пере-даваемого по данной дуге от её начала к её концу. Условие (1) выражает ограничение на поток по каждой дуге: нельзя передать больше, чем эта дуга может пропустить. Условие (2) выражает закон сохранения: сколько продукта поступило в промежуточную вершину, столько же оттуда отправлено далее.
Величиной Р (u) потока u называется сумма потоков во всех дугах, выходящих из источ-ника, т.е. общее количество передаваемого по сети продукта.
Пример 2. Для иллюстрации введённых понятий рассмотрим сеть, показанную на рис. 2.
Векторы
u 1 = (2, 0, 1, 1, 1, 0, 0, 2, 0);
u 2 = (0, 1, 0, 0, 0, 1, 1, 1, 0);
u 3 = (1, 0, 1, 0, 0, 1, 0, 0, 1);
u 4 = (2, 1, 1, 1, 1, 1, 0, 2, 1)
являются различными потоками в этой сети (проверьте это!). Легко видеть, что
Р (u 1) = 2, Р (u 2) = 1, Р (u 3) = 2, Р (u 4) = 3
Интересно изобразить эти четыре потока графически, сопоставив каждой единице потока по дуге пунктирную линию вдоль этой же дуги. Такое представление дается на рис.3.
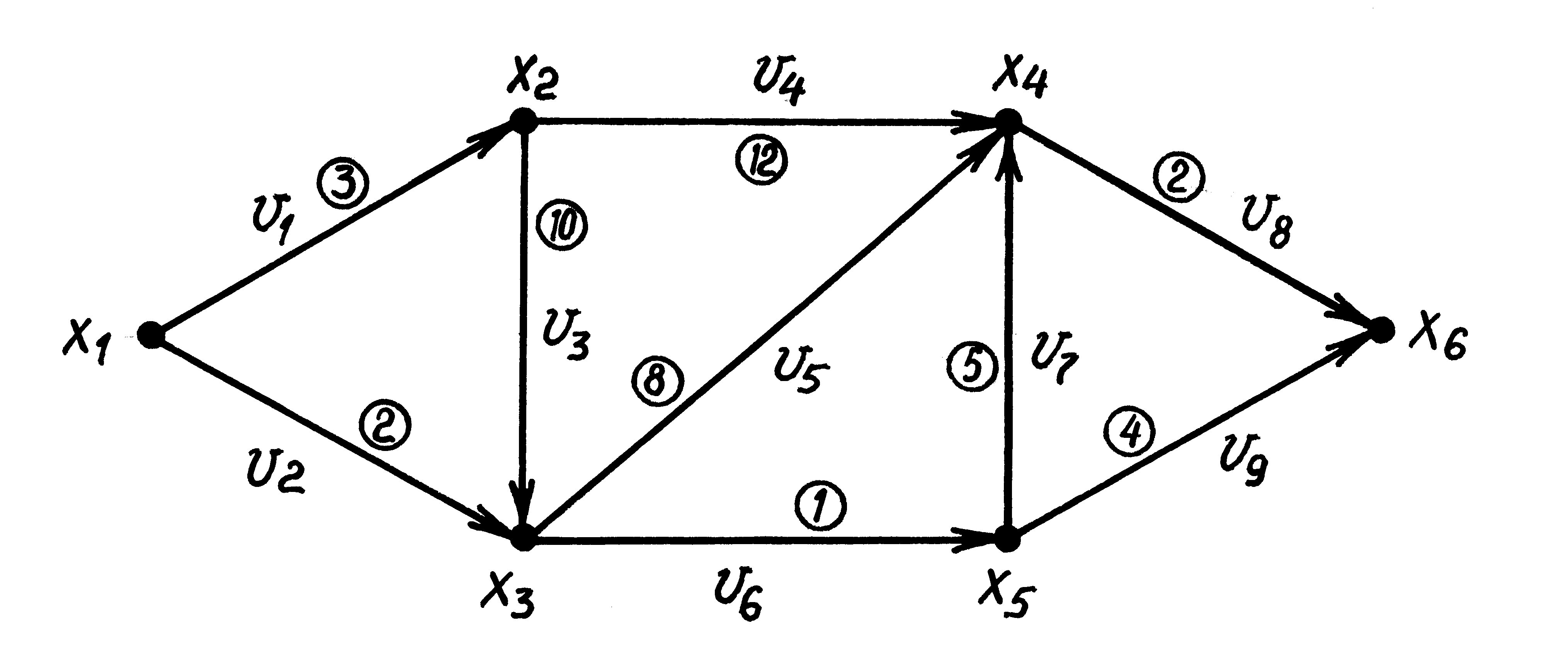
Рис.2 ■
Рис.3
Задание 1. Установить, является ли указанный вектор потоком в сети, изображённой на рис.2. В случае положительного ответа представить данный поток графически, как сделано в примере 2 (см. рис.3).
u 1 = (0, 0, 0, 0, 0, 0, 0, 0, 0);
u 2 = (1, 0, 1, 0, 1, 0, 0, 1, 0);
u 3 = (0, 1, 0, 0, 1, 0, 0, 1, 0);
u 4 = (0, 1, 0, 0, 0, 1, 0, 0, 1);
u 5 = (1, 1, 0, 1, 1, 0, 0, 2, 0);
u 6 = (1, 2, 0, 1, 1, 1, 0, 2, 1);
u 7 = (3, 0, 1, 2, 0, 1, 0, 2, 1);
u 8 = (0, 2, 0, 0, 2, 0, 0, 2, 0);
u 9 = (1, 2, 0, 1, 1, 1, 0, 2, 1);
u 10 = (1, 1, 1, 0, 2, 0, 0, 2, 0) ■
