Вершина j графа (орграфа) называется достижимой из вершины i, если существует путь (орпуть) с началом в i и концом в j. Множество K вершин графа (орграфа) называется компо-нентой связности (сильной связности), если любые две вершины из K взаимно достижимы, и при этом множество K является максимальным по включению множеством, обладающим дан-ным свойством (это означает, что при добавлении к K хотя бы одной новой вершины свойство взаимной достижимости теряется). Заметим, что множество, состоящее из одной вершины, яв-ляется связным (в орграфе – сильно связным) в «силу ложности посылки», но далеко не всегда является компонентой связности (сильной связности), поскольку не обязано быть максималь-ным по включению. Заметим также, что множество всех вершин графа (орграфа) также не обя-зано быть компонентой связности (сильной связности). Если же граф (орграф) состоит из един-ственной компоненты, то он называется связным (сильно связным).
Пример 20. Рассмотрим граф, показанный на рис.19 (копия рис.7-f). У него есть три ком-поненты связности: { A, B, C, D }, { E, F, G, H, I, J }, { R }■
Пример 21. Рассмотрим орграф, показанный на рис.20 (копия рис.10-6). В нём вершины 1 и 3 взаимно достижимы (с помощью дуг a и b), поэтому они по определению входят в одну и ту же компоненту сильной связности. Каждая из вершин 2 и 4 образует отдельную компоненту сильной связности, поскольку из 3 нельзя перейти в 4, а из 4 нельзя перейти в 2. Таким образом, у данного графа имеется три компоненты сильной связности: {1, 3}, {2} и {4}■
Задание 10. Найти компоненты связности в графах на рис.7 ■
Задание 11. Найти компоненты сильной связности в орграфах на рис.10 ■
Наличие нескольких кратных рёбер и любого числа петель, естественно, никак не сказы-вается на компонентах связности ни в неориентированном, ни в ориентированном случае. Поэ-тому в обоих случаях для нахождения компонент связности можно преобразовать граф к прос-тому графу без петель, оставив по одному ребру (дуге) среди нескольких кратных и удалив все петли.
 Рис.19
Рис.19
|  Рис.20
Рис.20
|
Пример 22. Граф, показанный на рис.21a (копия рис.5-12), не является простым и содер-жит петлю при вершине. После удаления кратной дуги и петли (а также введения нумерации вершин) получается простой граф, показанный на рис.21b, в котором, как и в исходном графе, имеется одна компонента связности.
 Рис.21a
Рис.21a
|  Рис.21b
Рис.21b
|
Пример 23. Орграф, показанный на рис.20, не является простым, поскольку дуги c и d кратны. После удаления одной из кратных дуг получается простой орграф, показанный на рис.22. В нём, как и в исходном орграфе, содержатся те же компоненты сильной связности: {1, 3}, {2} и {4}. Заметим, что дуги a и b в исходном орграфе не являются кратными, в отличие от дуг c и d ■

Рис.22
Задание 12. Привести все графы на рис.5, 7 и орграфы на рис.10, которые содержат крат-ные дуги и/или петли к простым графам (орграфам) без петель. В качестве ответов нарисовать пару «исходный-изменённый граф» и описать изменёный граф (орграф) парой á V, E ñ (á V, А ñ), как это делалось в примерах 4 – 6 ■
Компоненты связности (сильной связности) в небольших графах, показанных на рис.7 и 10, находятся непосредственно (как говорят, «глазами»). Надо сказать, что «глазами» выполня-лись и все предыдущие задания этой главы. Однако ведущую роль в решении прикладных задач дискретного характера играют алгоритмы. Конечно, алгоритмы для решения всех приведённых выше заданий хорошо известны. В этом разделе излагается алгоритм нахождения компонент связности неориентированных графов. Учитывая суть задания, можно обойтись простыми гра-фами без петель. Аналогичный алгоритм для орграфов здесь не излагается.
Прежде, чем перейти к формальным конструкциям, рассмотрим следующий
Пример 24. На рисунке 23 показан граф, содержащий 300 вершин и около 1200 рёбер. Число компонент связности в нём равно двум. Однако даже в данном, сравнительно простом, случае проверить это «глазами», мягко говоря, затруднительно ■
4.1. Алгоритм нахождения компонент связности простых неориентированных гра-фов. Когда речь заходит о каких бы то ни было алгоритмах, первым – и часто определяющим вопросом – является вопрос о формальном представлении рассматриваемых объектов или, как часто говорят, о выборе соответствующей структуры данных. В разделе 1.1 было дано формаль-ное представление простых неориентированных графов в виде пары á V, E ñ, где V = {1, 2, …, n } – множество вершин графа, E  V *2, где V *2 – множество всех одно- и двухэлементных подмно-жеств множествавершин V. Двухэлементное множество { x, y }, принадлежащее E, интерпрети-руется как ребро с концами x и y.
V *2, где V *2 – множество всех одно- и двухэлементных подмно-жеств множествавершин V. Двухэлементное множество { x, y }, принадлежащее E, интерпрети-руется как ребро с концами x и y.
Однако в данном случае, как и во многих других, более адекватной структурой данных яв-ляется следующая. Граф задаётся в виде массива, i -ый элемент которого соответствует вершине i. Сам же i -ый элемент является массивом, состоящим из номеров всех вершин, смежных с вер-

Рис.23
шиной i. В рамках такой структуры удобно просматривать все вершины, смежные с данной, чем и оправдано их применение. Такое представление графов назовём массивом смежных вершин.
Для орграфов аналогичное представление определяется как массив, i -ый элемент которого является массивом номеров всех вершин, в которые ведёт дуга из вершины i.
Пример 25. Для графа, показанного на рис.6, массив смежных вершин имеет следующий вид:
áá2, 4, 5ñ, á3, 4, 5ñ, á2, 4ñ, á2, 3, 5ñ, á1, 2, 4ññ■
Пример 26. Для графа, показанного на рис.24 (полученным из графа на рис.19 перенуме-рацией вершин), указанное представление имеет следующий вид:áá2, 3, 4ñ, á1, 3ñ, á1, 2, 4ñ, á1, 3ñ, á6, 8, 9ñ, á5, 7, 10ñá6, 8ñ, á5, 7ñ, á5ñ, á6ñ, áññ. Обратите внимание на последний (11-ый) массив: поскольку вершина 11 изолирована, список смежных с ней вершин пуст ■
Пример 27. Для графа, показанного на рис.25 (копия рис.10-5), указанное представление имеет следующий вид: áá3, 4ñ, á1, 4ñ, á2, 4ñ, áññ. На 4-ой позиции стоит пустой кортеж, так как из вершины 4 не выходит ни одна дуга.
Задание 13. Все графы и орграфы, полученных в результате выполнения задания 12, пред-ставить в виде массива смежных вершин (см. примеры 25 – 27) ■
 Рис.24
Рис.24
|  Рис.25
Рис.25
|
Далее рассматривается основной материал данного раздела. Предлагается алгоритм, по массиву смежных вершин определяющий компоненты связности графа. Суть его такова. Опре-делим массив M длины n (через n обозначено число вершин графа). Присвоение i -ой вершине метки а означает формальную операцию присвоения M [ i ] = а. Начинаем с любой вершины (для определённости, с первой). Присваиваем ей метку -1.
Пусть некоторое множество вершин имеет метки -1 и +1. Возьмём любую вершину x с меткой -1 (если таковая найдётся) и у всех вершин, смежных с ней и ещё не имеющих метку, поставим метку -1. После этого, независимо от того, была ли помечена хотя бы одна вершина, у вершины x заменим метку -1 на +1. Если же ни одной вершины с меткой -1 не найдётся, то все вершины с меткой +1 образуют 1-ую компоненту связности. Если больше непомеченных вер-шин нет, то граф состоит из одной компоненты связности. Если есть хоть одна непомеченная вершина y, то пометим её меткой -2 и повторим весь процесс с заменой 1 на 2. Далее, если ещё остались непомеченные вершины, пометим любую из них меткой -3, и т.д, вплоть до того, когда все вершины становятся помеченными. При этом все вершины с одной и той же меткой i обра-зуют i -ую компоненту связности.
Пример 28. Применим описанный алгоритм для графа из примера 26 (рис.24). Для него массив смежных вершин таков: áá2, 3, 4ñ, á1, 3ñ, á1, 2, 4ñ, á1, 3ñ, á6, 8, 9ñ, á5, 7, 10ñá6, 8ñ, á5, 7ñ, á5ñ, á6ñ, áññ.
1. Инициализация. В данном случае число вершин равно 11. Поэтому определим массив M длины 11 и положим M [1] = -1.
2. В соответствии с алгоритмом положим M [2] = -1, M [3] = -1, M [4] = -1.
3. Поскольку помечены все вершины из списка смежных с вершиной 1 вершин 2, 3, 4, то
положим M [1] = 1.
4. Возьмём следующую вершину 2 с меткой -1. Смежные с ней вершины 1, 3 уже помече-ны. В соответствии с алгоритмом положим M [2] = 1.
5. Возьмём следующую вершину 3 с меткой -1. Смежные с ней вершины 1, 2, 4 уже поме-чены. В соответствии с алгоритмом положим M [3] = 1.
6. Возьмём следующую вершину 4 с меткой -1. Смежные с ней вершины 1, 3 уже помече-ны. В соответствии с алгоритмом положим M [4] = 1.
7. Поскольку более вершин с меткой -1 нет (M [1] = M [2] = M [3] = M [4] = 1), то выбираем следующую непомеченную вершину 5 и присваиваем ей метку M [5] = -2.
8. В соответствии с алгоритмом для смежных с вершиной 5 вершин 6, 8, 9 положим M [6] = -2, M [8] = -2, M [9] = -2.
9. Поскольку помечены все вершины из списка смежных с вершиной 5 вершин 6, 8, 9, то
положим M [5] = 2.
10. Возьмём следующую вершину 6 с меткой -2. Смежными с ней вершинами является 5 (уже помеченная), а также 7 и 10 (ещё непомеченные). В соответствии с алгоритмом положим M [7] = -2, M [10] = -2.
11. В соответствии с алгоритмом положим M [6] = 2.
12. Возьмём следующую вершину 7 с меткой -2. Смежными с ней вершинами является 6 и 8 (уже помеченные). В соответствии с алгоритмом положим M [7] = 2.
13. Возьмём следующую вершину 8 с меткой -2. Смежными с ней вершинами является 5 и (уже помеченные). В соответствии с алгоритмом положим M [8] = 2.
14. Возьмём следующую вершину 9 с меткой -2. Смежной с ней вершинами является только 5 (уже помеченная). В соответствии с алгоритмом положим M [9] = 2.
15. Возьмём следующую вершину 10 с меткой -2. Смежной с ней вершинами является только 6 (уже помеченная). В соответствии с алгоритмом положим M [10] = 2.
16. Поскольку вершин с меткой -2 нет (M [5] = M [6] = M [7] = M [8] = M [9] = M [10] = 2), то выбираем следующую непомеченную вершину 11 и присваиваем ей метку M [11] = -3.
17. В соответствии с алгоритмом просматриваем все вершины, смежные с 11. Поскольку вершин, смежных с 11, не существует, то меняем метку M [11]: M [11] = 3.
18. Поскольку более вершин с меткой -3 не существует, то в соответствии с алгоритмом ищем непомеченную вершину. Так как таковых не имеется, то алгоритм останавливается.
После остановки имеем следующий массив M: M = á1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3ñ. Это и означает, что 1-ую компоненту связности образуют вершины 1, 2, 3, 4; 2-ую компоненту связности – вершины 5, 6, 7, 8, 9, 10; 3-ью компоненту связности – изолированная вершина 11■
Задание 14. Для всех неориентированных графов, рассмотренных в задании 13, найти указанным алгоритмом компоненты связности (см. пример 28) ■
Число вершин, смежных любой вершине графа, называется степенью данной вершины.
Эйлеровы циклы
5.1. Кёнигсбергские мосты. Не каждому городу выпадает честь быть отмеченным в та-кой точной науке, как классическая математика. Кёнигсберг же благодаря своим мостам и вели-кому учёному-математику XVIII-го века Леонарду Эйлеру вошёл в число математических зна-менитостей.
 Рис.26. Великий математик Леонард Эйлер (1707 – 1783)
Рис.26. Великий математик Леонард Эйлер (1707 – 1783)
|
 Рис.27. Кенигсберг начала XVIII века с мостами
Рис.27. Кенигсберг начала XVIII века с мостами
|
Леонард Эйлер (Leonhard Euler) родился 15 апреля 1707 г. в маленькой тихой Швейцарии, куда изо всей Европы приезжали мастера и учёные, не желавшие тратить дорогое рабочее вре-мя на частые в других странах гражданские смуты и религиозные распри. Так переселилась в Базель из Голландии и семья Бернулли, давшая миру уникальное созвездие научных талантов во главе с братьями Якобом и Иоганном. Семья небогатого протестантского пастора Пауля Эй-лера жила в доме Бернулли. Иоганн Бернулли быстро заметил и оценил талант Леонарда, стал его наставником, а сыновья Иоганна Николай и Даниил – его друзьями.
Более всего поражает способность великого учёного говорить о сложных вещах простым языком. Для решения серьёзных математических задач Эйлер использовал наглядные голово-ломки. Одна из них положила начало совершенно новой области исследований, выросшей впос-ледствии в самостоятельный раздел математики – теорию графов. Особенность этой теории – в геометрическом подходе к изучению объектов. Живя в Кёнигсберге, прогуливаясь по его набе-режным, Эйлер обратил внимание на оригинальное расположение семи мостов города. Причи-ной этому было причудливое течение рукавов Прегеля, соединенных протокой, охватывающих с севера и юга остров Кнайпхоф, а затем сливающихся вместе (рис.27). Эти мосты назывались так:
1. Kramer-Brucke (Лавочный мост)
2. GruneBrucke(Зелёный мост)
3. Kottel-Brucke(Потроховый мост)
4. Schmiede-Brucke(Кузнечный мост)
5. Holz-Brucke(Деревянный мост)
6. Hohe-Brucke(Высокий мост)
7. Honig-Brucke(Медовый мост)
В 1736 Эйлер решил задачу, известную с тех пор как задача о кенигсбергских мостах:можно ли пройти по всем этим мостам и при этом вернуться в исходную точку так, чтобы по каждому мосту пройти только один раз. На рис.28 изображена условная схема семи мостов Кё-нигсберга (заметим, что сейчас осталось только два из них).
Упростим схему, показанную на рис.28. Для этого представим каждый из четырёх участ-ков суши одной точкой, а каждый из мостов – линией, соединяющей соответствующие точки. В результате получаем граф, показанный на рис.3. Обратим внимание на то, что данный граф не

Рис.28
является простым (см. пример 2). Нетрудно понять, что исходная задача стала значительно бо-лее обозримой. В уже введённых терминах (см. раздел 4) вопрос ставится так: существует ли в графе на рис.3 цикл, проходящий по всем рёбрам? Напомним, что однократность прохождения каждого ребра включена в определение цикла в разделе 4. Эйлер дал общий ответ на поставлен-ный вопрос в следующем виде.
Теорема. Для того чтобы данный связный граф имел цикл, проходящий по всем рёбрам, необходимо и достаточно, чтобы степени всех вершин графа были чётными. Для того чтобы данный связный граф имел цепь между вершинами А и В, проходящую по всем рёбрам, необхо-димо и достаточно, чтобы степени всех вершин, кроме А и В, были чётными, а степени этих вершин были нечётными.
Поскольку в графе на рис.3 степени некоторых вершин нечётны, то, следовательно, требу-емого цикла не существует. В честь Эйлера циклы в неориентированных графах, проходящие по всем рёбрам, были названы эйлеровыми циклами, как и соответствующие цепи.
5.2. Алгоритм Флёри. Теорема Эйлера сама по себе является теоремойсуществования: в ней не говорится о том, как построить эйлеров цикл. Эффективный алгоритм был предложен французским математиком Флёри в 1873 году – почти через 150 лет после открытия Эйлера. Для его изложения нам понадобится важное понятие перешейкав графе. Перешеек – это ребро, удаление которого разделяет связную компоненту графа на две несвязные части.
Пример 29. Найдём все перешейки в графе, показанном на рис.29 a. Граф состоит только из одной компоненты связности, так что надо найти каждое ребро, удаление которого делает граф несвязным.

Рис.29
Ребро {3, 5} является перешейком; его удаление делает граф несвязным, как показано на рис. 29 b. Ребро {7, 8} также является перешейком; его удаление делает граф несвязным, как показа-но на рис.29 c; при этом вершина 8 образует отдельную компоненту связности. Удаление ребра {6, 7} не приводит к разделению графа, как показано на рис.29 d; то же самое относится к удалению любого ребра (кроме {3, 5}и {7, 8}).
Алгоритмтм Флёри.
1. Начинаем с любой вершины. Проходим вдоль любого ребра до другой вершины. Запомина-ем это ребро как начало цикла и удаляем его из графа.
2. Пусть мы достигли некоторой вершины. Выбираем любое выходящее из неё ребро, с одним условием: не выбираем перешеек, если есть другая возможность. Проходим вдоль выбранного ребра до другой вершины. Добавляем это ребро в цикл и удаляем его из графа.
3. Выполняем шаг 2 до тех пор, пока не удалим все рёбра из графа.
Пример 30. Применималгоритм Флёри к графу, показанному на рис.30 a. Прежде всего проверяем, что граф связен и степени всех вершин чётны. По теореме Эйлера из этого следует, что эйлеров цикл в таком графе должен быть.

Рис.30
Начинаем процесс с вершины 3. Из 3 можно двигаться либо в 2, либо в 5. Пойдём по на-правлению к 5, удалив ребро {3, 5} (на рисунке 30 b указаны номера удаляемых рёбер в порядке их удаления). Таким образом, началом искомого цикла является ребро {3, 5}. Далее можно дви-гаться в вершины 4, 6 или 7. Поскольку ни одно из рёбер {5, 4}, {5, 6} и {5, 7} в графе после удаления ребра {3, 5} не является перешейком, то можно выбрать в качестве 2-го ребра цикла любое из этих трёх рёбер. Выбираем ребро {5, 7}. На рис.30 b это ребро имеет номер 2, а начало искомого цикла выглядит так: 3→5→7.
Далее, из вершины 7можно перейти в вершины 1, 4 или 6. Однако ребро {7, 1} является перешейком в графе, полученном удалением рёбер {3, 5} и {5, 7} (см. рис.30 b). Так как есть другие возможности ({7, 4} и {7, 6}), в соответствии с алгоритмом Флёри выберем одну из них. Выбрав {7, 6 }, продлеваем строящийся цикл этим самым ребром {7,6} и получаем 3→5→7→6; удаляемые рёбра и модифицированный граф показаны на рис.30 b. Заметим, что выбор пере-шейка {7, 1} в графе, показанном на рис.30 b, и его последующее удаление привели бы к невоз-можности когда-либо пройти по рёбрам {7, 4} и {7, 6}. Это поясняет условие на шаге 2 алго-ритма Флёри.
Граф, оставшийся после удаления первых трёх рёбер искомого цикла – {3, 5}, {5, 7} и {7,6} – показан на рис.30 с. Из очередной вершины 6 в графе рис.30 с выходит только одно ребро {6,5}, которое является перешейком в этом графе. В соответствии с алгоритмом Флёри, мы должны двигаться далее по этому ребру {6,5}, несмотря на то, что {6,5} является перешейком, так как других возможностей нет. Далее все последующие рёбра определяются также совер-шенно однозначно (см. рис.30 с). В результате получаем эйлеров цикл 3→5→7→6→5→4→7→
1→2→3. В него по одному разу входят все 9 рёбер рассматриваемого графа. Полная последова-тельность удаляемых по порядку рёбер представлена на рис.30 d.
Задание 15. В неориентированных графах, показанных на рис.31, найти эйлеров цикл, пользуясь алгоритмом Флёри. Решение должно быть представлено, как в примере 30. Это озна-чает, что должны быть подробно показаны все шаги и должны быть отмечены все встречаемые перешейки, вплоть до ситуации, когдадальнейшие рёбра определяются совершенно однознач-но ■
Двудольные графы
В заключение данной главы рассмотрим один специальный класс простых неориентиро-ванных графов – так называемые двудольные графы. Они широко используются в приложени-ях. Граф называется двудольным, если множество его вершин можно разбить на два непустых подмножества (доли), так что любое его ребро соединяет две вершины из разных долей (эквива-лентно: концы любого ребра принадлежат разным долям). Из этого определения следует, что двудольный граф не содержит петель. Множество рёбер двудольного графа, которые не имеют общих вершин, называется паросочетанием. Паросочетание, содержащее максимальное число рёбер, называется максимальным паросочетанием. Алгоритмы поиска максимальных (а также некоторых других) паросочетаний рассмотрены в части «Дискретная оптимизация» и в части «Модели конфликта и взаимодействия» настоящего пособия.
Пример 31. Двудольный граф показан на рис.32. Множество X = {{1,7}, {3,11}, {5,10}}, состоящее из трёх рёбер является паросочетанием, поскольку входящие в него рёбра не имеют общих концов. Множество Y = {{4,7}, {1,8}, {3,9}, {5,10}, {6,11}}, состоящее из пяти рёбер, также является паросочетанием. Его максимальность следует из того, что «нижняя» доля со-держит 5 вершин, в силу чего паросочетаний, состоящий более чем из 5 рёбер, просто не сущес-твует – если бы оно было, то по крайней мере два его ребра были бы инцидентны одной верши-не, что противоречит определению паросочетания ■



Рис.31
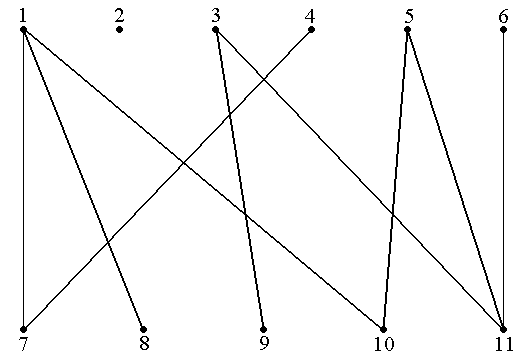
Рис.32. Двудольный граф
Задания
Задание 1. По заданному формальному описанию нарисовать граф (см. примеры 1, 3 – 5).
1. G = á V, E, F ñ, где V = {1, 2, 3, 4}, E ={ a, b, c, d, e, f, g, h }, F (a) = F (b) = {1, 3}, F (c) = F (d) = {2, 4}, F (e) = {2, 3}, F (f) = {1, 4}, F (g) = {3, 4}, F (h) = {1, 2}.
2. G = á V, E ñ, где V = {1, 2, 3, 4}, E = {{1, 2}, {2, 3}, {3, 4}, {1, 4}, {2, 4}}.
3. G = á V, E, F ñ, где V = {1, 2, 3}, E ={ a, b, c, d, e, f }, F (a) = F (b) = {1, 2}, F (c) = F (d) = {1, 3}, F (e) = F (f) = {2, 3}.
4. G = á V, E, F ñ, где V = {1, 2, 3}, E ={ a, b, c, d, e }, F (a) = F (b) = {1, 2}, F (c) = F (d) = {1, 3}, F (e) = {2, 3}.
5. G = á V, E ñ, где V = {1, 2, 3, 4}, E = {{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}.
6. G = á V, E ñ, где V = {1, 2, 3, 4, 5, 6}, E = {{2}, {6}, {1, 4}, {1, 5}, {1, 6}, {2, 5}, {3, 6}}.
7. G = á V, E, F ñ, где V = {1, 2, 3, 4}, E ={ a, b, c }, F (a) = F (b) = {1, 2}, F (c) = {3, 4}.
8. G = á V, E ñ, где V = {1, 2, 3, 4, 5, 6, 7}, E = {{7}, {1, 2}, {2, 3}, {3, 4}, {5, 6}, {1, 6}}.
9. G = á V, E ñ, где V = {1, 2, 3, 4, 5}, E = {{5}, {1, 2}, {2, 3}, {3, 4}, {4, 5}, {1, 5}}.
10. G = á V, E, F ñ, где V = {1, 2, 3}, E ={ a, b, c, d, e }, F (a) = F (b) = {1, 2}, F (c) = {1, 3}, F (d) = {2, 3}, F (e) = {3}.
11. G = á V, E, F ñ, где V = {1, 2}, E ={ a, b, c }, F (a) = F (b) = F (c) = {1, 2}.
12. G = á V, E ñ, где V = {1, 2, 3, 4}, E = {{1, 2}, {2, 3}, {3, 4}, {1, 4}, {2, 4}, {1, 3}}.
13. G = á V, E ñ, где V = {1, 2, 3, 4, 5, 6}, E = {{1, 4}, {1, 5}, {1, 6}, {2, 4}, {2, 5}, {2, 6}, {3, 4}, {3, 5}, {3, 6}}.
14. G = á V, E, F ñ, где V = {1, 2, 3, 4}, E ={ a, b, c, d }, F (a) = F (b) = {1, 3}, F (c) = {1, 4}, F (d) = {2, 3}.
15. G = á V, E, F ñ, где V = {1, 2, 3, 4}, E ={ a, b, c, d, e }, F (a) = {1, 4}, F (b) = {1, 2}, F (c) = {3, 4}, F (d) = F (e) = {2, 3} ■
База 1 неориентированных графов для заданий 2,

| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|

| 
| 
|
Задание 2. Графы, включённые в базу 1, задать парами á V, E ñ или тройками á V, E, F ñ (см. примеры 1, 3 – 5)■

Задание 3а. Вграфах, показанных на рис.5, найти все максимальные по включению внут- ренне устойчивые множества вершин, все минимальные по включению внешне устойчивые
множества вершин и все ядра ■
Задание 4. В графах из базы орграфов найти все ядра, или убедиться в их отсутствии ■
Предметный указатель
Граф, двудольный
неориентированный
ориентированный
Графа, вершина
дуга
дуги кратные
компонента связности
перешеек
ребро
рёбра кратные
ядро
Множество вершин внешне устойчивое
внутренне устойчивое
Мультиграф
Орграф
Орграфа, компонента сильной связностисвязности
Орпуть в орграфе
Орпуть в орграфе, циклический
Орцепь
Орцикл
Орцикл, простой
Паросочетание
максимальное
Петля при вершине
Путь в графе
Путь в графе, обратный
циклический
эйлеров
Цепь
Цикл
Цикл, простой
эйлеров
Число внешней устойчивости
внутренней устойчивости
Глава 7. Потоки в сетях
1. Определение потоковой сети
2. Задача о максимальном потоке
3. Модификация основной постановки
4. Поиск максимального потока
6. Предметный указатель
Во многих практически важных случаях функционирование системы, моделируемой ори-ентированным графом, определяется передачей между её отдельными частями (которым сопо-ставлены вершины графа) некоторых потоков (материальных, энергетических, информацион-ных). Теория, в рамках которой изучаются распределения потоков, называется теорией потоков в сетях. Распределение потоков во многих случаях оценивается некоторым числом, характери-зующим эффективность данного распределения. Поэтому задача оптимизации распределения потоков является одной из основных задач теории потоков в сетях. Формальной постановке и решению базовой задачи этой теории - задаче о максимальном потоке - и посвящена настоя-щая глава.






