Дадим определения сразу для неориентированного и ориентированного случаев, учиты-вая, что эти определения очень похожи (отличия будем указывать в скобках). Две различные вершины, которые соединены ребром (дугой), т.е. являющиеся концами одного и того же ребра (дуги), называются смежными. В противном случае две вершины не смежны. Множество X вершин графа G, любые две из которых не смежны, называется внутренне устойчивым, а мак- симально возможное число элементов внутренне устойчивого множества − числом внутренней устойчивости графа G (обозначается α (G)).
Сразу поясним это не очень простое понятие. Прежде всего, любое множество вершин, со-стоящее из одной вершины, является по определению внутренне устойчивым как в неориенти-рованном, так и в ориентированном случае. Действительно, определение внутренней устойчи-вости множества вершин X, как и почти все математические определения, является импликаци-ей. Его можно переформулировать так: «Если любые две разные вершины множества X не смежны, то множество X называется внутренне устойчивым» или, пользуясь определёнными в главе 1-4 кванторами, короче
(
a Î X)( b Î X)[(a ≠ b)→(a не смежна с b)]. (3)
Но если множество X состоит из одной вершины, то посылка a ≠ b импликации (3) всегда ложна, поскольку a и b – две разные вершины из множества X. Напомним, что по определению импли-кации (см. раздел 1-2.1.4), импликация с ложной посылкой всегда истинна «в силу ложности посылки». Но это и означает истиннось импликации (3), что и означает внутреннюю устойчи-вость любого одноэлемнтного множества.
Утверждение 1. Любое подмножество внутренне устойчивого множества внутренне ус-тойчиво
Действительно, по определению, во внутренне устойчивом множестве никакие две верши-ны не соединены ребром. Значит, этим же свойством обладает и любое его подмножество ■
Внутренне устойчивое множество вершин называется максимальным по включению, ес-ли оно не содержится ни в каком другом внутренне устойчивом множестве. Утверждение 1 позволяет при поиске всех внутренне устойчивых множеств ограничиться поиском только максимальных по включению внутренне устойчивых множеств. Действительно, всякое внут-ренне устойчивое множество либо само является максимальным по включению, либо содержит-ся в некотором максимальном по включению внутренне устойчивом множестве. (Заметим, что таких множеств может быть несколько). Поэтому семейство всех максимальных по включению внутренне устойчивых множеств определяет все внутренне устойчивые множества: множество является внутренне устойчивым, если оно содержится хотя бы в одном максимальном по вклю-чению внутренне устойчивом множестве.
Пример 7. Проиллюстрируем понятия внутренней устойчивости множества вершин в не-ориентированном графе. Для этого рассмотрим граф, показанный на рис.5а. На рис.5б – 5е по-казаны все максимальные по включению внутренне устойчивые множества в данном графе. На каждом из этих рисунков видно, что все выделенные большими кружками вершины не соедине-ны непосредственно друг с другом рёбрами. Ясно также, что при добавлении любой вершины все эти множества перестают быть внутренне устойчивыми – появляются рёбра. Обратим вни-мание на то, что максимальные по включению внутренне устойчивые множества могут содер-жать различное число вершин – три на рис.5б – 5г и два на рис.5д и 5е.
Множество, показанное на рис.5ж, является внутренне устойчивым, но не максимальным по включению. Оно содержится в множестве, показанном на рис.5б. Наконец, множество, пока-занное на рис.5з, не является внутренне устойчивым. Входящие в него вершины 5 и 6 соедине-ны ребром.
Поскольку максимальное число вершин во внутренне устойчивом множестве равно 3, то число внутренней устойчивости α (G) = 3.
Рис.5а. Исходный граф
| 
Рис.5б. Максимальное по включению
внутренне устойчивое множество {1,3,4}
|
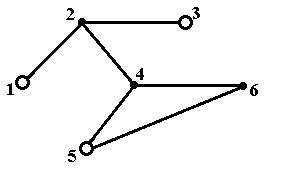Рис.5в. Максимальное по включению
внутренне устойчивое множество {1,3,5}
| 
Рис.5г. Максимальное по включению
внутренне устойчивое множество {1,3,6}
|
Рис.5д. Максимальное по включению
внутренне устойчивое множество {2,5}
| 
Рис.5е. Максимальное по включению
внутренне устойчивое множество {2,6}
|
Рис.5ж. Внутренне устойчивое множество {1,4}, не максимальное по включению
| 
Рис.5з. Множество вершин {2,5,6}, не являющееся
внутренне устойчивым
|
Можно проверить, что любое множество, содержащее 4 вершины, не будет внутренне ус-тойчивым. Действительно, любое внутренне устойчивое множество не может содержать ника-ких двух вершин из подмножества {4,5,6}, так как они все попарно смежны (соединены рёбра-ми). Значит, в него может входить не более одной вершины из множества {4,5,6}. Но так как в нём должно быть 4 вершины, а всего есть 6 вершин, то в него должны входить все вершины из множества {1,2,3}. А так как вершины 1 и 2 смежны, то такое множество не может быть внут-ренне устойчивым. В силу того же утверждения 1 бóльшие множества вершин также не могут быть внутренне устойчивыми ■
В произвольном графе с небольшим числом вершин максимальные по включению внут-ренне устойчивые множества могут быть найдены простым перебором всех различных подмно-жеств, начиная с множества всех вершин. Однако самый простой и эффективный подход – вни-мательно посмотреть на граф собственными глазами (и подумать собственной головой). Конеч-но, в графах, содержащих порядка 15 и более вершин, такой просмотр практически нереален. Формальные алгоритмы решения данной задачи в силу своей сложности здесь не рассматрива-ются.
Введём дальнейшие понятия. Множество X вершин графа G называется внешне устойчи-вым, если любая вершина из V 
X, т.е. вершина, не принадлежащая X, смежна хотя бы с одной вершиной из X (является концом некоторой дуги, начало которой принадлежит множеству вер-шин X, в ориентированном случае). Минимально возможное число элементов внешне устойчи-вого множества называется числом внешней устойчивости графа G (обозначается β (G)). Об-ратим внимание на то, что связность вершин внутри множества X не оказывает никакого влия-ния на данное свойство. Это значит, что добавление или удаление любого ребра (дуги) между вершинами из X не повлияет ни на наличие свойства внешней устойчивости у множества X, ни на его отсутствие. Обратим внимание, что в определении не требуется, чтобы какая-нибудь вер-шина из X была бы смежной со всеми вершинами из V X. Достаточно, если любая вершина из V X смежна хотя бы с какой-нибудь вершиной из X. Для разных «внешних» вершин (т.е. из V X) смежные с ними «внутренние» вершины (т.е. из X) могут (но не обязаны!) быть различны-ми.
Заметим, что само множество всех вершин V является внешне устойчивым в силу ложнос-ти посылки. Действительно, при X = V имеем V X = Æ, т.е. вершин, не принадлежащих X, прос-то не существует. Как и определение внутренне устойчивого множества, определение внешне устойчивого множества является импликацией:
( a Î V X)→(
b Î X)(a смежна с b), (4)
которая всегда верна при ложной посылке ( a Î V X).
Имеет место простое
Утверждение 2. Любое множество, содержащее внешне устойчивое множества вершин, также внешне устойчиво.
Действительно, пусть внешне устойчивое множество X Í Y. Для всякой вершины z Î V Y верно z Î V X. Так как X – внешне устойчивое множество, то, по определению, z смежна с неко-торой вершиной w Î X (является концом дуги с началом w). А в силу включения X Í Y имеем w Î Y. Таким образом, начав с произвольной вершины z Î V Y, установили, что она смежна с некоторой вершиной w Î Y (является концом дуги с началом w), что, по определению, означает внешнюю устойчивость Y ■
Внешне устойчивое множество называется минимальным по включению, если оно не содержит ни одного другого внешне устойчивого множества. В силу утверждения 2, для нахож-дения всех внешне устойчивых множеств достаточно найти только минимальные внешне ус-тойчивые множества. Все остальные являются произвольными множествами, содержащими хо-тя бы одно минимальное по включению внешне устойчивое множество.
Проиллюстрируем теперь это понятие на том же графе рис.5а.
Пример 8. На рис.6а – 6е показаны все минимальные по включению внешне устойчивые множества в данном графе. На каждом из этих рисунков видно, что любая вершина, показанная чёрным кружком (как в исходном графе) соединена хотя бы с одной вершиной из внешне ус-тойчивого множества, выделенных квадратами. Ясно также, что при удалении любой вершины из внешне устойчивого множества все эти множества перестают быть внешне устойчивыми – появляются вершины, не соединённые ни с одной из оставшихся вершин. Обратим внимание на то, что минимальные по включению внешне устойчивые множества могут содержать различное число вершин – две на рис.6а – 6в и три на рис.6г – 6е.
Множество, показанное на рис.6ж, является внешне устойчивым, но не минимальным по включению. Оно содержит множества, показанные на рис.6б и 6в. Наконец, множество, пока-занное на рис.6з, не является внешне устойчивым. Вершина 3 не соединена ребром ни с верши-ной 1, ни с вершиной 4, что противоречит определению внешне устойчивого множества.
Поскольку минимальное число вершин во внешне устойчивом множестве равно 2, то чис-ло внешней устойчивости β (G) = 2.
Рис.6а. Минимальное по включению
внутренне устойчивое множество {2,4}
| 
Рис.6б. Минимальное по включению
внутренне устойчивое множество {2,5}
|
Рис.6в. Минимальное по включению
внутренне устойчивое множество {2,6}
| 
Рис.6г. Минимальное по включению
внутренне устойчивое множество {1,3,4}
|
Рис.6д. Минимальное по включению
внутренне устойчивое множество {1,3,5}
| 
Рис.6е. Минимальное по включению
внутренне устойчивое множество {1,3,6}
|
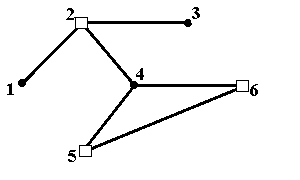Рис.6ж. Внешне устойчивое множество {2,5,6}, не минимальное по включению
| 
Рис.6з. Множество вершин {1,4}, не являющееся
внешне устойчивым
|
Видно непосредственно на рисунке, что любое множество, содержащее одну вершину, не будет внешне устойчивым – просто потому, что в исходном графе нет ни одной вершины, со-единённой со всеми остальными ■
Как и для внутренне устойчивых множеств, формальные алгоритмы решения данной зада-чи в силу своей сложности здесь не рассматриваются.
Множество X вершин графа G, одновременно внутренне и внешне устойчивое, называет-ся ядром графа G.
Напомним, что определения внутренне устойчивого множества вершин в неориентрован-ном и ориентированном случаях совпадают. Совпадают и определения ядра. Отличаются толь-ко определения внешне устойчивого множества: в ориентированном случае требуется, чтобы дуга, соединяющая множества X и V X, имела направление от X к V X.
Из определений внутренней и внешней устойчивости непосредственно следует, что:
- любая изолированная вершина графа может быть добавлена к любому не содержащему её внутренне устойчивому множеству и это расширенное множество также будет внутренне устойчивым;
- любое внешне устойчивое множество обязано содержать любую изолированную верши-ну.
Из утверждений 1 и 2 непосредственно следует
Утверждение 3. Множество вершин Z является ядром графа G тогда и только тогда, когда существуют минимальное по включению внешне устойчивое множество X и максимальное по включению внутренне устойчивое множество Y, такие, что
X 
Z Y. (5)■
Если уже известны все минимальные по включению внешне устойчивые множества X 1, …, Xs и все максимальные по включению внутренне устойчивые множества Y 1, …, Yt, то утвер-ждение 3 позволяет предложить следующий
А лгоритм нахождения всех ядер графа.
1. Находим все такие пары индексов i, j, такие, что Xi Yj.
2. Для каждой такой пары индексов находим все множества Z, удовлетворяющие двойно-му включению
Xi Z Yj. (6)
3. Из всех множеств Z, найденных на шагах 1 и 2, выделяем все различные множества. Они и являются всеми ядрами графа ■
Алгоритм применим как в неориентрованном, так и в ориентированном случаях. Если включение Xi Yj ни при каких i, j не выпоняется, то это означает, что в данном графе или орграфе ядер не существуют. Заметим также, что сами списки X 1, …, Xs и Y 1, …, Yt никогда не являются пустыми, поскольку в любом графе и орграфе любое одноэлементное множество яв-ляется внутренне устойчивым, а множество всех вершин – внешне устойчивым, в силу ложнос-ти посылки.
ккогда не выпоняется (например, если
Среди внешне усточЗаметим, что утверждения 1 – 4 верны как в неориентированном, так и в ориентированном случаях. Однако следующее утверждение верно только для неориентированных графов.
Утверждение 5. Любое максимальное по включению (т.е. не содержащееся ни в каком другом) внутренне устойчивое множество является и внешне устойчивым, т.е. является ядром ■
Поскольку в любом неориентированном (как и в любом ориентированном) графе множес-тво, состоящее из одной вершины, является внутренне устойчивым, то существует и макси-мальное по включению внутренне устойчивое множество. А оно, в силу утверждения 5, являет-ся ядром.
Утверждение 5 даёт гарантию существования ядра для неориентированных графов. А простой пример отсутствия ядра в орграфе даётся ниже, в прмере 10.
Пример 9. Рассмотрим снова граф на рис.5а. Максимальными по включению внутренне устойчивыми множествами являются множества {1,3,4}, {1,3,5}, {1,3,6}, {2,5}, {2,6} (см. рис. 5). Минмальными по включению внешне устойчивыми множествами являются множества {2, 4}, {2,5}, {2,6}, {1,3,4}, {1,3,5}, {1,3,6} (см. рис.6). В силу утверждения 4 любое ядро содержит-ся в некотором множестве из 1-го списка и содержит некоторое множестве из 2-го списка. В данном случае имеется пять таких множеств, причём во всех 5-и случаях оба включения (5) вы-полняются как равества:
{2,5} Z {2,5}, {2,6} Z {2,6}, {1,3,4} Z {1,3,4}, {1,3,5} Z {1,3,4},{1,3,4} Z {1,3,4}.
Поэтому множества вершин {2,5}, {2,6},{1,3,4}, {1,3,5}, {1,3,6} представляют собой все ядра в данном графе ■
Пример 10. На рис.7 показан орграф из примера 6 (сеть питания) с пронумерованными вершинами 1 – 5. В этом орграфе внутренне устойчивыми множествами являются все 1-элемен-тные множества {1}, {2}, {3}, {4}, {5} и 2-элементные множества {1,3}, {1,4}, {2,4}, {4,5}. Других внутренне устойчивых множеств в данном орграфе нет. Максимальными по включению являются только эти множества.
Одноэлементных внешне устойчивых множеств в данном случае нет (так как нет ни одной вершины, откуда дуги ведут во все остальные). Единственным двухэлементным внешне устой-чивым множеством является {1, 4} (так как дуги á1, 5ñ, á1, 2ñ и á4, 3ñ ведут из {1, 4} в 5, 2 и 3, т.е. во все остальные вершины, в соответствии с определением). В силу включений (5) единственным ядром является множество {1,4}, так как только оно удовлетворяет этим включениям ■
Само существование ядра для орграфов, в отличие от неориентированных графов, как ука-зывалось выше, не гарантировано, что демонстрирует следующий
Пример 11. Рассмотрим простой орграф без петель, показанный на рис.8. Проверим, что у
него нет ядра. Предположим, что ядро состоит из одной вершины 1. Но тогда нет дуги, ведущей из 1 в 3, т.е. оно не является внешне устойчивым. Аналогично, ядро не может состоять из вер-шины 2 или вершины 3. Предположим, что ядро состоит из двух вершин, скажем, вершин 1 и 2. Тогда есть дуга из 2 в 3, т.е. оно является внешне устойчивым. Но оно не является внутренне устойчивым, так как в него входят вершины 1 и 2, соединённые дугой. Аналогично для мно-жеств {1, 3} и {2, 3}. Наконец, множество всех вершин {1, 2, 3} является внешне устойчивым, но не является внутренне устойчивым. Таким образом, в данном орграфе ядер нет ■
Рис.7
| 
Рис.8
|
Задание 3. Ворграфах, показанных на рис.10, найти
1) одно максимальное и одно минимальное по числу вершин ядро;
2) если все ядра содержат одно и то же число вершин, найти два разных ядра;
3) если имеется всего одно ядро, найти его;
4) если ядер не существует, объяснить этот факт ■
Пути в графах
Как и в разделе 2, будем давать определения сразу для неориентированного и ориентиро-ванного случая, указывая отличия в скобках. Наиболее общим понятием является понятие пути (орпути). Путём (орпутём) в графе (орграфе) называется чередующаяся последовательность μ вершин и рёбер (дуг), начинающаяся и кончающаяся в вершинах:
μ = á v 0, b 1, v 1, b 2,..., vk -1, bk, vk ñ, (4)
такая, что вершины vi и vi +1 соединены ребром (дугой) bk.
Вершина v 0 называется началом пути (орпути) μ, вершина vk – концом пути (орпути) μ, а число k, равное числу рёбер (дуг), входящих в путь (орпуть) – его длиной. Говорят также, что путь μ соединяет вершины v 0 и vk (орпуть μ ведёт из v 0 в vk). Обратным путём для пути μ на- зывается путь μ -1 = á vk, bk, vk -1, bk -1,..., v 1, b 1, v 0ñ. Другими словами, путь μ -1состоит из тех же самых вершин и рёбер, но проходимых в обратном порядке. Обратим внимание, что обратный путь определён только в неориентированном случае.
Цепью (орцепью) называется путь (орпуть), в котором все рёбра (дуги) различны. Прос-
Рис.7
|
Рис.8
|
Рис.9
| ||
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
| 
| 
| |
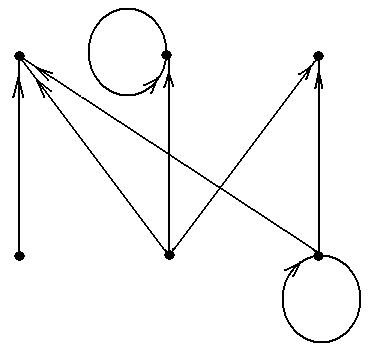
Рис. 10
той цепью (орцепью) называется цепь (орцепь), в которой все вершины различны. Путь (ор-путь), в котором начало и конец совпадают, называется циклическим путём (орпутём). Цик-лический путь, являющийся цепью (орцепью), называется циклом (орциклом). Цикл (орцикл), в котором все вершины, кроме начала и конца, различны и не совпадают с началом, называется простым циклом (орциклом).
Говорят, что не циклический путь ν содержится в не циклическом пути μ, если последова-тельность ν или последовательность ν -1 является подпоследовательностью последовательности μ. В ориентированном случае остаётся только часть этого определения: не циклический орпуть ν содержится в не циклическом пути орпути μ, если последовательность ν является подпоследо-вательностью последовательности μ.
Для циклических путей последнее определение требуется модифицировать, учитывая то, что такой путь можно «обходить», начиная с любой вершины, отчего он, конечно же, не изме-нится. Поэтому можно дать такие четыре определения:
1) не циклический путь ν содержится в циклическом пути μ, если последовательность μ можно циклически перенумеровать так, что последовательность ν или последовательность ν -1 станет подпоследовательностью этой перенумерованной последовательности μ;
2) не циклический орпуть ν содержится в циклическом орпути μ, если последовательность μ можноциклически перенумеровать так, что последовательность ν станет подпоследователь-ностью этой перенумерованной последовательности μ;
3) циклический путь ν содержится в пути μ, если последовательность ν или последова-тельность ν -1 можноциклически перенумеровать так, что эта перенумерованная последователь-ность ν станет подпоследовательностью последовательности μ;
4) циклический орпуть ν содержится в орпути μ, если последовательность ν можноцикли-чески перенумеровать так, что эта перенумерованная последовательность ν станет подпоследо-вательностью последовательности μ.
Эти на первый взгляд сложные понятия разъясняются далее (см. пример 13).
Все вышеприведённые в данном разделе понятия относятся к произвольным графам и ор-графам (см. раздел 1.1). В случае простых графов и орграфов понятие пути (орпути) упрощает-ся: под путём (орпутём) понимается последовательность вершин
μ =á v 0, v 1,..., vk -1, vk ñ, (5)
такая, что множество вершин { vi, vi +1} определяет ребро графа (петлю, если vi и vi +1 совпадают)
(пара вершин á vi, vi +1ñ определяет дугу орграфа (петлю, если vi и vi +1 совпадают)). Напомним, что в простых графах (орграфах) пара вершин однозначно определяет ребро (дугу), в то время как в графах общего вида таких рёбер (дуг) может быть несколько (см. рис.3, а также рис.5.1 и
10.1). Соответственно упрощаются все остальные приведённые выше определения – достаточно указывать только последовательности вершин.
Приведём примеры, иллюстрирующие и разъясняющие введённые понятия.
Пример 10. В графе, показанном на рис.11 (копия рис.5-6), обратным к пути μ = á1, f, 4, d, 2, c, 4, g, 3ñ является путь μ -1= á3, g, 4, c, 2, d, 4, f, 1ñ. Обратным к циклическому пути μ =á1, f, 4, d, 2, e, 3, b, 1ñ является циклический путь μ -1 = á1, b, 3, e, 2, d, 4, f, 1ñ (проверьте!) ■
Пример 11. В графе, показанном на рис.12 (копия рис.5-7), обратным к простому пути μ = á2, 1, 4, 3ñ является путь простой путь μ -1 = á3, 4, 1, 2ñ. Обратным к циклическому пути μ -1 = á2, 4, 1, 3, 4, 2ñ является циклический путь μ -1 = á2, 4, 3, 1, 4, 2ñ■
Пример 12. В графе, показанном на рис.13 (копия рис.5-3) последовательность μ = á1, d, 3,
e, 2, b, 1, a, 2, b, 1, c, 3ñ является путём с началом в вершине 1 и концом в вершине 3. Его длина, т.е. число входящих в него рёбер, равно 6. Этот путь не является цепью, так как не все его рёбра различны (ребро b встречается два раза). В этом же графе последовательность ν = á1, d, 3, e, 2, b, 1, c, 3ñ является цепью с началом в вершине 1 и концом в вершине 3. Эта цепь не является простой, так как в ней не все вершины различны (вершины 1 и 3 встречаются по два раза). По-следовательность λ = á1, d, 3ñ является простой цепью. Последовательность λ* = á1, c, 3ñ также является простой цепью, отличной от простой цепи λ = á1, d, 3ñ (см. рис.13). Заметим, что все четыре рассмотренных в примере пути μ, ν, λ, λ* соединяют одну и ту же пару вершин 1 и 3 ■
Пример 13. Граф, показанный на рис.14 (копия рис.7-c) является простым графом, поэто-му для задания путей можно пользоваться упрощёнными последовательностями, состоящими
Рис.11
| 
Рис.12
|
только из вершин. Последовательность μ = á D, C, G, E, C, B, G, E, F ñ является путём с началом в
вершине D и концом в вершине F; его длина равна 8. Путь μ не является цепью, так как ребро { G, E } входит в него дважды. Последовательность ν = á D, C, G, E, C, B, F ñ является цепью, так как все её рёбра не повторяются (проверьте!), но она не является простой цепью, так как вершина C встречается в ней два раза. Последовательность λ = á D, C, B, F ñ является простой цепью, поскольку все её вершины различны. Заметим, что все три рассмотренные пути – μ, ν, λ – соединяют одну и ту же пару вершин D и F ■
Рис.13
| 
Рис.14
|
Замечания в конце примеров 12 и 13 приводят к достаточно простому умозаключению, сформулированному в следующем утверждении.
Утверждение 6. Д ля всякого пути (орцепи), соединяющего две разные вершины, есть содержащаяся в нём цепь (орцепь), соединяющая те же две вершины. Для всякой цепи (орцепи), соединяющей две вершины, есть содержащаяся в ней простая цепь (орцепь), соединяющая те же две вершины ■
Заметим, что существующая в силу утверждения 6 цепь может совпадать с содержащим её путём (если сам путь уже является цепью); существующая в силу утверждения 6 простая цепь может совпадать с содержащей её цепью (если сама эта цепь уже является простой цепью).
Пример 14. В графе, показанном на рис.15 (копия рис.5-15) последовательность μ = á1, a, 2, b, 1, a, 2ñ является путём. Этот путь не является цепью, поскольку он проходит два раза по ребру a. Двумя содержащимися в этом пути цепями являются только цепи ν = á1, a, 2ñ и ν * = á1, b, 2ñ. Обе эти цепи уже являются простыми, и поэтому любая содержащаяся в одной из них простая цепь совпадает с содержащей цепью ■
Заметим также, что во всех рассмотренных в примерах 12 − 14 путях начальная и конеч-ная вершины всегда различны, т.е. ни один из них не является циклическим путём.
Задание 4. Вграфах, показанных на рис.5, найти
1) путь, не являющийся цепью;
2) содержащуюся в найденном в 1) пути цепь, не являющуюся простой, соединяющую те же самые вершины;
3)содержащуюся в найденной в 2) цепи простую цепь, соединяющую те же самые верши-ны.
Если некоторые искомые объекты не существуют (как в примере 14), то объяснить это ■
Задание 5. Вграфах, показанных на рис.7, найти
1) путь, не являющийся цепью;
2) не содержащуюся в найденном в 1) пути цепь, не являющуюся простой;
3) не содержащуюся в найденной в 2) цепи простую цепь.
Если некоторые искомые объекты не существуют, то объяснить это ■
Пример 15. Рассмотрим простой граф, показанный на рис.16 (копия рис.5-9). Не цикли-
ческий путь μ = á6, 2, 5ñ содержится в циклическом пути ν = á2, 5, 3, 6, 2ñ, хотя последователь-ность μ не является подпоследовательностью последовательности ν. Действительно, если тот же самый циклический путь ν начать с вершины 6, т.е. записать в виде ν = á6, 2, 5, 3,6ñ, то после такой перенумерации последовательность μ становится подпоследовательностью последова-тельности ν. Рассмотрим теперь не циклический путь μ = á4, 1, 5ñ и циклический путь ν = á1, 4, 2, 5, 1ñ. Последовательность á4, 1, 5ñне является подпоследовательностью ни самой последова-тельности ν,ни любой её циклической перестановки: á4, 2, 5, 1, 4ñ, á2, 5, 1, 4, 2ñ, á5, 1, 4, 2, 5ñ. Однако обратная последовательность μ -1= á5, 1, 4ñ содержится в циклически переставленной ν = á4, 2, 5, 1, 4ñ, и, значит, в силу введённых определений, путь μ = á4, 1, 5ñ содержится в цикли-ческом пути ν ■
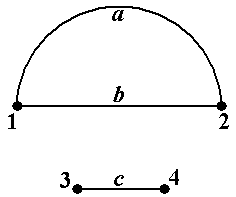Рис.15
| 
Рис.16
|
Пример 16. В графе, показанном на рис.13, последовательность μ = á1, d, 3, е, 2, е, 3, с, 1, b, 2, a, 1ñ является циклическим путём, но не является циклом, поскольку ребро е входит в него дважды. Содержащийся в пути μ путь ν = á1, d, 3, с, 1, b, 2, a, 1ñ является циклом, но не является простым циклом, так начальная и конечная вершина 1 входит в него 3 раза, вместо двух, требу-емых определением. Наконец, содержащийся в пути ν путь λ = á1, d, 3, с, 1ñ является простым циклом ■
Пример 17. В графе, показанном на рис.14, последовательность μ = á E, C, G, B, A, F, B, G, E ñ является циклическим путём, но не является циклом, поскольку ребро { G, B } входит в него дважды. Содержащийся в пути μ путь ν = á E, C, B, A, F, B, G, E ñ является циклом, но не является простым циклом, так вершина B входит в него 2 раза. Наконец, содержащийся в пути ν путь λ = á E, C, B, G, E ñ является простым циклом ■
Имеет место утверждение, аналогичное утверждению 7 для не циклических путей.
Утверждение 7. Д ля всякого циклического пути (орпути) есть содержащийся в нём цикл (орцикл). Для всякого цикла (орцикла) есть содержащийся в нём простой цикл (орцикл) ■
Задание 6. Вграфах, показанных на рис.5, найти
1) циклический путь, не являющийся циклом;
2) содержащийся в найденном в 1) пути цикл, не являющийся простым;
3) содержащийся в найденном в 2) цикле простой цикл.
Если некоторые искомые объекты не существуют, то объяснить это ■
Задание 7. Вграфах, показанных на рис.7, найти
1) циклический путь, не являющийся циклом;
2) не содержащийся в найденном в 1) пути цикл, не являющийся простым;
3) не содержащийся в найденном в 2) цикле простой цикл.
Если некоторые искомые объекты не существуют, то объяснить это ■
Пример 18. В орграфе, показанном на рис.17 (копия рис.10-3) последовательность μ = á1, b, 2, a, 1, d, 3, c, 1ñ является циклическим орпутём, который является орциклом. Этот орцикл содержит два простых цикла: ν 1 = á1, b, 2, a, 1ñ и ν 2 =á 1, d, 3, c, 1ñ. Кроме них, в данном орграфе есть простой орцикл á1, d, 3, e, 2, a, 1ñ■
Пример 19. В орграфе, показанном на рис.18 (копия рис.10-4) имеется два орцикла: á1, 2, 3, 4, 5, 6, 1ñ и á7, 7ñ. Они оба являются простыми орциклами ■
|
Рис.17
|
Рис.18
|
Задание 8. Ворграфах, показанных на рис.10, найти
1) циклический орпуть, не являющийся орциклом;
2) содержащийся в найденном в 1) орпути орцикл, не являющийся простым;
3) содержащийся в найденном в 2) орцикле простой орцикл.
Если некоторые искомые объекты не существуют, то объяснить это ■
Задание 9. Ворграфах, показанных на рис.10, найти
1) циклический орпуть, не являющийся орциклом;
2) не содержащийся в найденном в 1) пути орцикл, не являющийся простым;
3) не содержащийся в найденном в 2) орцикле простой орцикл.
Если некоторые искомые объекты не существуют, то объяснить это ■
Введём ещё одно важное для дальнейшего понятие. Граф (орграф) называется ациклич-ным, если он не содержит циклов (орциклов). Рассмотрим подробнее ацикличные орграфы. В ацикличном орграфе по самому определению отсутствуют орциклы и, следовательно, все орпу-ти являются простыми. Однако для ацикличных орграфов верен и более специальный факт, в каком-то смысле описывающий их структуру. Имеет место
Утверждение 8. Пусть G (V, A) – простой ацикличный граф с множеством вершин V и множеством дуг A. Тогда множество вершин V разбивается на непересекающиеся подмножест-ва V 1, …, Vm, такие, что для любой дуги (p, q) графа G начало p содержится в множестве Vi c бóльшим номером, чем конец q.
Доказательство этого утверждения, по сути, является алгоритмом построения указанных подмножеств. Поскольку граф ацикличен, то в нём найдётся хотя бы одна дуга, из которой не выходят дуги. Обозначим множество всех таких вершин через V 1. Удалим из графа G все вер-шины из V 1 и все ведущие в них дуги. Оставшийся граф также будет ацикличным. Множество его вершин, из которых не выходят дуги, обозначим через V 2. Продолжая этот процесс, полу-чим разбиение с требуемыми свойствами (последний оставшийся граф Gm не может содержать дуг, иначе на нём процесс не мог бы окончиться) ■
