Пусть на тело массой m действует сила F. Запишем второй закон Ньютона для тела:
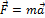
Преобразуем его:
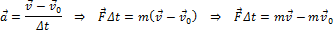
Мы получили второй закон Ньютона, записанный в другом виде. Величина
называется импульсом тела. Импульс тела – величина векторная. Единица измерения импульса тела в системе СИ не имеет своего индивидуального наименования, а выражается через другие единицы: [кг·м/с] = [Н·с]. Величина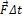 
- произведение силы на время ее действия называется импульсом силы. Итак, второй закон Ньютона можно записать через импульс:
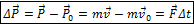
Читается так: изменение импульса тела равно импульсу действующей на него силе. Если на тело действует несколько сил, то под F понимается их равнодействующая.
*) Если действующая на тело сила непостоянна, то второй закон Ньютона можно писать только для бесконечно малого промежутка времени:
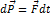
Для определения изменения импульса за конечный промежуток времени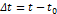 
необходимо разбить его на множество бесконечно малых промежутков, записать для каждого из них второй закон Ньютона и все эти уравнения сложить:
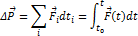
| F |
| t0 |
| t |
| t |
| FΔt |
Если известен график зависимости силы от времени, то импульс силы численно равен площади под графиком.
Пусть имеется система тел. Пусть массы тел равны: m1, m2, m3, …, а их скорости v1, v2, v3, … Импульсом системы тел называется векторная сумма импульсов всех тел системы:
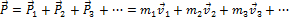
На каждое тело системы может действовать несколько сил. Пусть на первое тело системы действуют силы: F 11, F 12, F 13, …, на второе: F 21, F 22, F 23, …, на третье: F 31, F 32, F 33, … и так далее. Запишем второй закон Ньютона для всех тел системы для некоторого промежутка времени Δt:
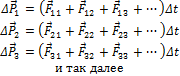
А теперь сложим все эти уравнения:
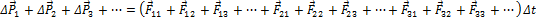
Короче это можно записать так:
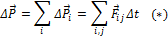
Здесь Δ Р – изменение суммарного импульса системы тел.
Разделим теперь все силы, действующие в нашей системе тел на две категории: внутренние и внешние силы. Внутренними назовем силы, с которыми тела, входящие в систему взаимодействуют между собой, а внешними – силы, с которыми тела, входящие в систему, взаимодействуют с телами, не входящими в систему. Рассмотрим внутренние силы системы. Пусть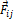 
– сила, действующая на i-ое тело со стороны j-ого тела системы. Согласно третьему закону Ньютона, в (*) должна существовать сила 
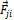, действующая на j-ое тело со стороны i-ого тела. Причем эти две силы равны по модулю и противоположны по направлению, а значит, их сумма равна нулю. Итак, для каждой внутренней силы по третьему закону Ньютона в (*) найдется парная ей сила такая, что сумма этих сил будет равна нулю. В результате, в (*) все внутренние силы уйдут и останутся только внешние силы. В конечном итоге получаем:
Изменение импульса системы тел равно суммарному импульсу всех внешних сил, действующих на систему.
Еще раз отметим, что изменение импульса каждого тела системы происходит под действием всех действующих на него сил: как внешних, так и внутренних, а изменение импульса всей системы происходит только под действием внешних сил. Внутренние силы системы тел на ее импульс никакого влияния не оказывают.
Системы тел, на которые не действуют внешние силы, называются замкнутыми. Если система тел замкнутая, то
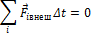
а значит изменение импульса замкнутой системы равно нулю. В этом и состоит закон сохранения импульса: импульс замкнутой системы тел есть величина постоянная. Аналитически закон сохранения импульса для системы тел записывается так:
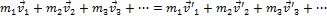
Слева от знака равенства начальный импульс системы, а справа – конечный.
Абсолютно замкнутых систем тел не существует. Однако на практике часто законом сохранения импульса пользоваться можно. Перечислим случаи, в которых на практике можно использовать закон сохранения импульса:
1) Если система не замкнута, но время взаимодействия тел системы очень мало, а возникающие при этом внутренние силы значительно превышают внешние силы. Сюда входят все задачи, связанные со столкновениями тел, с разрывами гранат и так далее.
2) Если система не замкнута, но в проекции на какое-то направление внешние силы равны нулю. Тогда в проекции на это направление можно использовать закон сохранения импульса. Например, в поле тяжести Земли на все тела действует сила тяжести и никакая система тел не может быть замкнутой. Однако проекция силы тяжести на любое горизонтальное направление равна нулю и если силами сопротивления можно пренебречь, то в проекции на горизонтальное направление импульс должен оставаться постоянным.
Центр масс
Рассмотрим движение системы двух тел. Запишем второй закон Ньютона для системы:
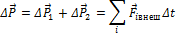
Заменим сумму внешних сил их равнодействующей: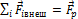 
. Получаем:
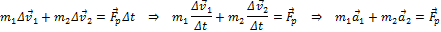
Перепишем последнее уравнение в виде:
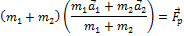
Обозначим:
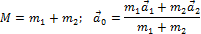
Получается:
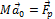
Полученное уравнение очень напоминает второй закон Ньютона для системы тел, так как М – это суммарная масса системы, F p – равнодействующая всех внешних сил, действующих на систему, а а 0 – величина, имеющая размерность ускорения. Эту величину можно рассматривать как некое усредненное ускорение системы тел. Аналогично можно ввести величину, определяющую некую усредненную скорость системы:
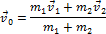
и величину, определяющую положение системы тел в пространстве:
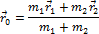
Все эти выражения можно написать для системы с произвольным количеством тел. Материальная точка, масса которой равна суммарной массе системы, а радиус-вектор определяется выражением:
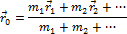
называется центром масс системы тел и характеризует распределение масс в системе. Аналогично, скорость, определяемая выражением:
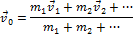
называется скоростью центра масс системы, а ускорение:
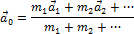
называется ускорением центра масс системы тел.
Таким образом, движение любой системы тел в целом можно описывать как движение материальной точки, называемой центром масс системы. Кроме того, можно сформулировать положение, которое называется теоремой о движении центра масс: центр масс системы тел движется так, как двигалась бы материальная точка, масса которой равна суммарной массе системы, под действием всех внешних сил, приложенных к системе. Если система тел замкнутая, то ее центр масс должен двигаться без ускорения, то есть равномерно и прямолинейно.
Реактивное движение
Всем известно так называемое явление отдачи. Если выстрелить из незакрепленной пушки, то пушка в результате отдачи после выстрела начнет двигаться в сторону противоположную скорости вылета снаряда. Если человек, стоя на гладком льду, оттолкнет от себя какой-либо тяжелый предмет, то сам начнет двигаться в противоположную сторону. Если надуть детский резиновый шарик и отпустить, то, выталкивая из себя воздух, сам шарик начнет быстро двигаться. На этом явлении отдачи основано реактивное движение.
В камере сгорания реактивного двигателя происходит сгорание топлива. Образовавшиеся при этом продукты сгорания (в основном газы) имеют очень большую температуру и с большой скоростью вылетают из сопла двигателя. При этом сам двигатель приобретает скорость отдачи. Если реактивный двигатель находится в космической ракете, то масса ракеты по мере сгорания топлива уменьшается. То есть сама ракета во время полета является телом переменной массы.
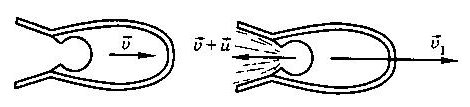Рассмотрим ракету, летящую в космосе вдали от звезд и планет. Пусть продукты сгорания вылетают из сопла ракеты с постоянной скоростью u относительно ракеты. Пусть в некоторый момент времени масса ракеты равна М, а ее скорость относительно инерциальной системы отсчета, связанной со звездами, равна v. Спустя очень маленький промежуток времени Δt масса ракеты станет равна 
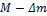(Δm – масса топлива, сгоревшего за время Δt), скорость ракеты немного возрастет и станет равна 
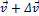, а сгоревшая масса топлива вылетит из сопла ракеты и будет иметь скорость 
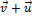. Так как система ракета – продукты сгорания изолированная, то должен выполняться закон сохранения импульса:
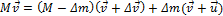
Раскрыв скобки и приведя подобные, получаем:
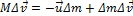
Так как Δt очень малая величина, то и Δm тоже очень малая величина. Значит последнее слагаемое в последнем уравнении является произведением двух очень малых величин (бесконечно малая второго порядка). Поэтому этим слагаемым можно пренебречь. Пусть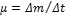 
- секундный расход топлива – масса топлива, сгорающая в единицу времени. Окончательно имеем:
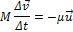
Это уравнение называется уравнением Мещерского. Величина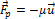 
называется реактивной силой. Она обусловлена отдачей при истечении продуктов сгорания из сопла реактивного двигателя. Она приложена к ракете и не зависит от устройства двигателя, а определяется только секундным расходом топлива и скоростью истечения газов из сопла. Направлена реактивная сила противоположно направлению скорости истечения газов.
Принцип реактивного движения заключается в том, что при истечении из сопла газы приобретают импульс. Согласно закону сохранения импульса ракета приобретает в противоположном направлении равный по модулю импульс.
Работа. Мощность
Если на тело действует постоянная сила F и тело совершает перемещение S, то величина
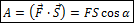
называется работой силы. Здесь α – угол между направлениями вектора силы и вектора перемещения. Работа – величина скалярная. Единицей измерения работы в системе СИ является Джоуль [Дж].
1 Дж = 1 Н·1 м
Один Джоуль – это работа, которую совершает сила 1 Н при перемещении тела на 1 м при условии что α = 0. Работа силы может быть положительной (если α < 90°), отрицательной (если α > 90°), а также равна нулю (если α = 90°). Если на тело действует несколько сил, а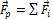 
- их равнодействующая, то работа равнодействующей равна:
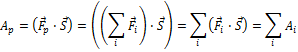
То есть, работа равнодействующей силы равна алгебраической сумме работ всех сил, действующих на тело. Если под действием постоянной силы тело совершает несколько перемещений, то суммарная работа будет равна алгебраической сумме работ на всех перемещениях:
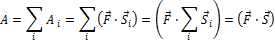
Здесь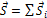 
- суммарное перемещение тела. Если сила постоянна, то работа этой силы при перемещении тела из начального положения в конечное не зависит от формы траектории, по которой двигалось тело, а определяется только суммарным вектором перемещения. В частности, работа постоянной силы при перемещении тела по произвольной замкнутой траектории всегда равна нулю.
Если действующая на тело сила не постоянна, то для нахождения ее работы весь участок движения необходимо разбить на маленькие участки Δ S i такие, что на каждом из них силу можно было бы считать постоянной, определить работу на каждом маленьком участке и все эти работы алгебраически сложить. Эта процедура фактически сводится к интегрированию.
| F |
| x1 |
| x2 |
| X |
| A |
Если работа А была совершена за промежуток времени Δt, то величина
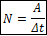
называется мощностью. Мощность, определяемая подобным образом, имеет смысл средней мощности на промежутке Δt. Если под действием силы F тело совершает перемещение S, то
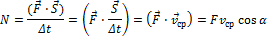
Здесь v ср – средняя скорость перемещения. Для определения мгновенной мощности надо перейти к пределу бесконечно маленьких промежутков времени:
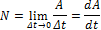
Для мгновенной мощности силы получаем:
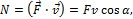
где v – мгновенная скорость; α – угол между векторами силы и скорости. Единицей измерения мощности в системе СИ является Ватт [Вт].
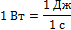
Кинетическая энергия
Пусть на тело массой m действует постоянная сила F. При этом тело движется равноускоренно с ускорением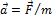 
. Пусть тело переместилось из начального положения в конечное, совершив перемещение S. Если начальная скорость тела на этом перемещении равна v0, а конечная – v, то можно написать:
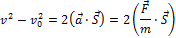
Это выражение можно переписать так:
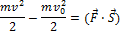
Справа от знака равенства записана работа силы F. Если на тело действует несколько сил, то вместо силы F можно написать равнодействующую всех этих сил. Величина
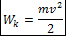
называется кинетической энергией тела. Существует теорема о кинетической энергии: работа равнодействующей силы при произвольном перемещении тела равна изменению кинетической энергии тела на этом перемещении. Кинетическая энергия – величина скалярная и всегда положительная. Единицей измерения кинетической энергии, так же как и работы является Джоуль [Дж].
Изменение кинетической энергии тела может быть как положительным, так и отрицательным. Так если некоторая сила совершает над телом положительную работу, то его кинетическая энергия возрастает. С другой стороны, если на движущееся тело начинает действовать тормозящая сила, то скорость тела, а значит и его кинетическая энергия начинает уменьшаться. При этом тело само совершает работу против силы сопротивления за счет своей кинетической энергии. Таким образом, наличие у тела кинетической энергии означает его способность совершать работу.
Потенциальная энергия
Рассмотрим еще один вид энергии, которая тоже характеризует способность тела совершать работу. Как уже упоминалось, если сила, действующая на тело, постоянна, то работа этой силы при перемещении тела из некоторого начального положения в конечное не зависит от формы траектории движения тела, а определяется только начальным и конечным состояниями. Дело в том, что таким свойством обладают очень многие и даже непостоянные силы. Все силы в природе можно разделить на два класса.
Силы, работа которых не зависит от формы траектории, а определяется только начальным и конечным состояниями тела, называются потенциальными или консервативными. Силы, работа которых зависит от формы траектории, называются непотенциальными или неконсервативными. Существует другой признак потенциальности силы: если работа силы при перемещении тела по произвольной замкнутой траектории равна нулю, то сила является потенциальной. Из известных нам механических сил гравитационная сила и сила упругости являются потенциальными, а сила трения – непотенциальной.
Пусть на тело действует некоторая потенциальная сила и тело перемещается из некоторого начального положения 1 в некоторое конечное положение 2. Потенциальная сила при этом совершает работу А12, которая не зависит от способа перемещения, а определяется только положениями 1 и 2. Если же перемещать тело из положения 1 в положение 3, то сила совершает работу А13, которая определяется только положениями 1 и 3. Так же со всеми перемещениями из точки 1 в любую другую точку. Таким образом, если на тело действует потенциальная сила, то можно выбрать некоторое начальное положение, а все остальные положения характеризовать работой, совершаемой этой силой при перемещении тела из выбранного начального положения в любое конечное. То есть любому положению тела можно приписать работу, совершаемую потенциальной силой при перемещении тела из определенного начального положения в это конечное. Эта работа служит определением потенциальной энергии. А именно: потенциальной энергией тела в некоторой точке поля действия потенциальной силы называется работа, совершаемая потенциальной силой при перемещении тела из некоторого определенного начального положения в данное конечное, взятая с обратным знаком. При этом потенциальная энергия тела в выбранном начальном положении равна нулю.
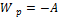
Так как начальное положение отсчета потенциальной энергии можно выбрать произвольно, то потенциальная энергия тела в любом положении зависит от произвольно выбранного начального положения. Таким образом потенциальная энергия тела оказывается величиной неопределенной или, как говорят, потенциальная энергия определена относительно произвольно выбираемого начального положения. Можно, конечно, договориться и выбрать за ноль потенциальной энергии какое-либо определенное положение. Иногда именно так и поступают. Однако на практике чаще всего этого делать не обязательно. Дело в том, что на практике обычно представляет интерес не сама потенциальная энергия, а ее изменение при перемещении тела. А вот изменение потенциальной энергии от выбора нулевого уровня не зависит.
Пусть в некотором положении 1 потенциальная энергия тела равна W1, а в положении 2 – W2. Это значит, что потенциальная сила при перемещении тела из начального положения в положение 1 совершает работу А1 = −W1, а в положение 2 – А2 = −W2. Однако перемещение тела из начального положения в положение 2 можно представить как перемещение тела сначала из начального положения в положение 1, а затем из положения 1 в положение 2. То есть можно написать: А2 = А1 + А12, где А12 – работа, совершаемая потенциальной силой при перемещении тела из положения 1 в положение 2. Получается:
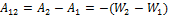
Работа потенциальной силы равна изменению потенциальной энергии, взятой с противоположным знаком.
Потенциальная энергия – величина скалярная и измеряется в Джоулях. Однако, в отличие от кинетической энергии, она может быть как положительной, так и отрицательной. Знак потенциальной энергии определяется выбором нулевого положения.
