Виды положений равновесия. Устойчивость тел

устойчивое

неустойчивое

безразличное

Положения равновесия бывают трех типов: устойчивые, неустойчивые и безразличные. Рассмотрим пример трех положений равновесия шарика, приведенный на рисунке. Если в первом положении (шарик в ямке) мы выведем шарик из положения равновесия, сместив его в сторону, то появляется так называемая скатывающая сила (как на наклонной плоскости), направленная в сторону положения равновесия. Если шарик отпустить, то эта сила обратно вернет его в положение равновесия. Такое положение равновесия называется устойчивым. Во втором положении (шарик на горке) при отклонении шарика в сторону также появляется скатывающая сила, но она направлена в сторону от начального положения и, если шарик отпустить, то он скатится с горки. Такое положение равновесия называется неустойчивым. В третьем положении при отклонении шарика от начального положения никаких новых сил не возникает и если шарик отпустить, то он останется в новом положении. Такое положение равновесия называется безразличным.

Дадим более строгое определение. Положение равновесия тела называется устойчивым, если при малом отклонении от положения равновесия возникают внешние силы, стремящиеся вернуть тело обратно в положение равновесия. Если же возникающие внешние силы стремятся увести тело еще дальше от положения равновесия, то такое положение равновесия называется неустойчивым. Если при отклонении тела никаких внешних сил не возникает, то положение равновесия безразличное.

Можно показать (и это хорошо видно на рисунке), что тип положения равновесия связан с характером изменения потенциальной энергии тела. Пусть тело находится в устойчивом положении равновесия. Это значит, что при отклонении тела в любую сторону от положения равновесия возникает сила, направленная к положению равновесия. При этом приходится совершить положительную работу против этой силы. Но работа внешней силы равна изменению потенциальной энергии тела. Значит, при отклонении тела от устойчивого положения равновесия потенциальная энергия тела увеличивается. То есть в устойчивом положении равновесия потенциальная энергия тела имеет минимум. Аналогично можно показать, что в неустойчивом положении равновесия потенциальная энергия тела имеет максимум. В безразличном положении равновесия потенциальная энергия постоянна.

Если у тела имеется устойчивое положение равновесия, то предоставленное самому себе, тело стремится в это положение равновесия, то есть стремится к минимуму потенциальной энергии. Это справедливо для любой системы тел. Можно сформулировать следующее положение: любая система тел, предоставленная самой себе, стремится занять положение, обладающее минимумом потенциальной энергии.

а)

б)

в)

mg

mg

mg

Рассмотрим устойчивость положения тела на горизонтальной или наклонной поверхности. Положим кирпич узким основанием на доску и начнем медленно приподнимать один конец доски. На рисунке представлены три варианта положения кирпича на доске. Интуитивно понятно, что в случае а) кирпич будет устойчиво лежать на доске, а в случае б) обязательно опрокинется. Это связано с тем, что в случае а) линия действия силы тяжести пересекает поверхность внутри площади опоры, а в случае б) вне площади опоры. В случае а) момент силы тяжести относительно крайней правой точки площади опоры направлен против часовой стрелки, а, значит, прижимает кирпич к поверхности, а в случае б) этот момент направлен по часовой стрелке, а, значит, опрокидывает кирпич. В случае с) линия действия силы тяжести проходит точно через границу площади опоры, а, значит, кирпич находится в состоянии неустойчивого равновесия. Аналогично рассматривается вопрос об устойчивости положения тел на горизонтальной поверхности. Этот вопрос может стоять при рассмотрении устойчивости наклонных тел (например, Пизанской башни) или тел неправильной формы (например, подъемного крана). В любом случае, для того, чтобы положение тела было устойчивым необходимо, чтобы линия действия силы тяжести пересекала поверхность внутри площади опоры.

 

ГИДРОСТАТИКА

Давление. Закон Паскаля

Гидростатика – раздел механики, в котором рассматриваются жидкости и погруженные в них тела, находящиеся в состоянии равновесия. Мы в дальнейшем будем рассматривать так называемую идеальную жидкость. Идеальной жидкостью называется несжимаемая и невязкая жидкость.

Силы, с которыми отдельные части жидкости действуют друг на друга и на стенки сосуда, аналогичны силам упругости, возникающим в твердых телах. Если в сжатой жидкости мысленно выделить какой-либо объем, то на него со стороны окружающей жидкости будут действовать силы упругости, зависящие от степени сжатия жидкости. Соответственно жидкость в выделенном объеме действует на окружающую жидкость. Причем силы упругости, возникающие в жидкости и в газе, всегда обусловлены только деформацией сжатия. Поэтому сила, действующая со стороны жидкости на любую выделенную поверхность внутри жидкости (или газа), а также на поверхность твердого тела всегда направлена перпендикулярно (нормально) к поверхности. Сил упругости, направленных по касательной к поверхности внутри идеальной жидкости нет.

Упругие напряжения внутри жидкости называются давлением. Если на поверхность площадью S со стороны жидкости действует сила давления F, то давлением называется отношение силы к площади поверхности:

Давление – величина скалярная. Единицей измерения давления в системе СИ является паскаль - [Па] = [Н/м²].

Основным законом гидростатики является закон Паскаля: давление внутри неподвижной жидкости передается одинаково во всех направлениях. То есть сила давления, действующая на небольшую площадку, находящуюся внутри жидкости, не зависит от пространственной ориентации площадки. Причем давление может быть обусловлено как силой тяжести самой жидкости, так и внешними силами, действующими на жидкость (например, атмосферное давление).

Далее рассмотрим следствия из закона Паскаля.

 

Гидростатическое давление

mg

F1

F2

h

Пусть однородная жидкость плотностью ρ находится в однородном поле тяжести. Выделим в жидкости тонкий вертикальный цилиндрический объем высотой h. На этот выделенный объем жидкости действуют: сила тяжести и силы давления со стороны окружающей жидкости. Силы давления окружающей жидкости на боковую поверхность цилиндра действуют со всех сторон одинаково и полностью друг друга компенсируют. Поэтому мы их далее рассматривать не будем. Остаются три силы: сила тяжести mg, сила давления на верхнее основание цилиндра F₁ и сила давления на нижнее основание цилиндра F₂. Так как выделенный объем жидкости находится в равновесии, то можно написать:

Если площадь сечения цилиндра равна S, то , , . Где ρ – плотность жидкости, Р ₁ и Р ₂ – давление жидкости на верхнее и нижнее основания цилиндра. В результате получаем:

Полученная формула называется формулой для гидростатического давления. Гидростатическое давление создается самой жидкостью в результате действия на нее силы тяжести. Если имеется свободная поверхность жидкости, давление на которой равно Р ₀ (чаще всего, атмосферное давление), то давление жидкости на глубине h равно:

Рассмотрим теперь свободную поверхность неподвижной жидкости. Выделим тонкий плоский приповерхностный элемент жидкости. На этот элемент действуют: сила тяжести mg и сила давления со стороны нижеле

mg

F

жащей жидкости F. Так как выделенный элемент находится в покое, то эти две силы должны компенсировать друг друга. Но сила давления направлена перпендикулярно нижней поверхности элемента. Значит и сила тяжести должна быть направлена перпендикулярно поверхности жидкости. Получается, что свободная поверхность неподвижной жидкости располагается всегда перпендикулярно направлению действия силы тяжести.

PAS

PBS

A

B

Рассмотрим неподвижную жидкость и две точки внутри жидкости А и В, находящиеся на одном горизонтальном уровне. Выделим в жидкости узкий цилиндрический объем, ось которого совпадает с прямой АВ, а торцевые поверхности перпендикулярны АВ. В горизонтальном направлении на выделенный цилиндр действуют только силы давления на торцевые поверхности: P_AS и P_BS, где Р_А и Р_В – давление жидкости в точках А и В. Так как выделенный объем находится в равновесии, то эти силы должны друг друга уравновешивать. Значит давление в точках А и В должно быть одинаковым. Можно сделать вывод: давление в однородной жидкости во всех точках, находящихся на одном горизонтальном уровне, одинаково.

Одним из известных следствий данного положения является то, что верхние уровни однородной жидкости в сообщающихся сосудах находятся на одинаковой высоте.

 

Закон Архимеда

Рассмотрим однородную неподвижную жидкость и погруженное в нее тело. На поверхность погруженного тела давит окружающаяся жидкость. Причем, давление окружающей жидкости зависит от глубины погружения данной точки поверхности. Давление жидкости увеличивается с глубиной погружения (гидростатическое давление). Значит, на нижнюю половину поверхности тела жидкость будет давить больше, чем на верхнюю половину. Значит, равнодействующая сил давления жидкости на поверхность погруженного в нее тела будет направлена вверх, то есть будет выталкивать тело из жидкости. Причем, сила давления окружающей жидкости на поверхность погруженного в нее тела не зависит от материала, из которого изготовлено тело. Мысленно вынем погруженное тело из жидкости и заполним освободившийся объем той же самой жидкостью. У нас получится однородная жидкость, находящаяся в равновесии. На объем жидкости, который ранее занимало погруженное тело, со стороны окружающей жидкости действуют те же самые силы давления. При этом этот объем жидкости находится в равновесии. Это значит, что равнодействующая сил давления окружающей жидкости полностью компенсируется силой тяжести выделенного объема жидкости. А это значит, что на тело, погруженное в жидкость, действует равнодействующая сил давления окружающей жидкости, равная силе тяжести этой жидкости в погруженном объеме тела. Эта сила называется силой Архимеда. Теперь можно сформулировать закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная силе тяжести жидкости в объеме погруженной части тела.

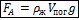
Здесь ρ_ж – плотность жидкости; V_пог – объем погруженной части тела.

Сила Архимеда, как и любая другая сила, имеет точку своего приложения. Точкой приложения силы Архимеда является центр тяжести жидкости в погруженном объеме тела.

Если тело опустить в жидкость, то оно либо плавает на ее поверхности, либо тонет. Это зависит от соотношения плотностей тела и жидкости. Если плотность тела меньше, чем плотность жидкости, то тело плавает на ее поверхности. При этом тело частично погружено в жидкость и его сила тяжести уравновешивается силой Архимеда:

Это уравнение называется условием плавания тела. Если плотность тела больше плотности жидкости, то тело тонет. При этом оно либо давит на дно сосуда, либо натягивает нить подвеса. Эта сила называется весом тела. Вес тела погруженного в жидкость равен разнице силы тяжести и силы Архимеда:

Заметим, что если тело плавает на поверхности жидкости, то его вес равен нулю.

 

Устойчивость плавания тел

mg

FA

N

O

O1

mg

mg

FA

FA

Рассмотрим устойчивость плавания тел на поверхности жидкости. Пусть на поверхности жидкости плавает однородный стержень, плотность которого меньше плотности жидкости. Имеется два положения равновесия плавания стержня: вертикальное и горизонтальное. Сила тяжести приложена в центре тяжести стержня, а сила Архимеда в центре тяжести погруженной части стержня. Если стержень находится в строго вертикальном, или в строго горизонтальном положении, то эти две силы направлены вдоль одной прямой и компенсируют друг друга. Однако, при случайных колебаниях поверхности воды, эти положения равновесия могут нарушиться и стержень отклонится в сторону. При этом возникнет момент силы тяжести и силы Архимеда. Из рисунка вино, что при отклонении стержня от вертикального положения этот момент сил будет опрокидывать стержень, а при отклонении от горизонтального положения будет возвращать его в исходное положение. Значит, вертикальное положение плавания стержня будет неустойчивым, а горизонтальное – устойчивым.

Вопросы устойчивости плавания очень важны при проектировании судов. Рассмотрим корабль, отклонившийся от вертикального положения. Пусть ось ОО₁ – ось симметрии корабля. Точка приложения силы тяжести находится на оси ОО₁, а силы Архимеда в центре тяжести погруженного объема корабля. Точка пересечения линии действия выталкивающей силы с осью ОО₁ (точка N) называется метацентром. Если метацентр находится выше точки приложения силы тяжести, то положение корабля устойчивое, а если ниже, то неустойчивое.

 

ГИДРОДИНАМИКА

Движение жидкости

Гидродинамика – часть механики, рассматривающая движение жидкости. Мы, в основном, будем говорить о жидкости, хотя многие положения могут быть применены и к движению газа. Газ отличается от жидкости тем, что он сжимаем. Однако при не очень высоких скоростях движения (по сравнению со скоростью звука) сжимаемость газов мала. Жидкости тоже сжимаемы, хотя их сжимаемость очень мала. Учет сжимаемости сильно усложняет рассмотрение движения жидкости и мы не будем ее рассматривать. Также очень усложняет рассмотрение движения жидкости ее вязкость. Вязкость связана с влиянием соседних слоев движущейся жидкости друг на друга. Однако вязкость воды (самой распространенной жидкости) довольно мала и при небольших скоростях течения ее влиянием можно пренебречь. Поэтому вязкость мы тоже учитывать не будем. Мы будем рассматривать только движение несжимаемой и невязкой, то есть идеальной жидкости.

Для визуального описания течения жидкости вводится понятие линии тока. В каждой точке движущейся жидкости проведем вектор скорости точек жидкости в данной точке и в данный момент времени. Проведем в жидкости линии такие, что касательная к линии в каждой точке совпадает по направлению с вектором скорости жидкости в данной точке. Такие линии называются линиями тока. Отдельные линии тока не пересекаются. При стационарном течении жидкости картина линий тока не изменяется. Часть жидкости, ограниченная линиями тока, называется трубкой тока.

Существует два качественно различных характера течения жидкости: ламинарное и турбулентное. При ламинарном течении скорости потока жидкости всегда направлены вдоль оси трубки тока. При ламинарном течении отдельные слои жидкости не перемешиваются, поэтому это течение еще называют послойным. Турбулентное течение – нерегулярное течение с завихрениями. При турбулентном течении отдельные слои жидкости перемешиваются. Возникновение завихрений в жидкости в основном связано с ее вязкостью и очень часто возникает при обтекании жидкостью различных препятствий. Так, например, медленное течение реки может быть ламинарным, однако при обтекании рекой ствола упавшего в нее дерева или сваи моста за препятствием наблюдаются завихрения. Турбулентное течение наиболее распространено и всегда возникает при увеличении скорости течения жидкости. Ламинарное течение может существовать только при небольших скоростях. Однако оно является наиболее простым движением жидкости и наиболее полно изучено. Турбулентное течение очень сложно для описания и на сегодняшний день полная теория турбулентного течения еще не создана. Поэтому мы в дальнейшем будем в основном рассматривать только ламинарное стационарное течение.

 

Уравнение неразрывности

S1

S2

v1

v2

v1Δt

v2Δt

Рассмотрим трубку тока и два ее произвольные сечения 1 и 2 площадью S₁ и S₂. Так как линии тока жидкости не пересекают поверхность трубки тока, то масса жидкости, которая за время Δt вошла в трубку через сечение S₁, равна массе жидкости, которая вышла из трубки через сечение S₂ за это же время. Если скорость потока жидкости в сечении 1 равна v₁, а в сечении 2 – v₂, то масса жидкости, которая за время Δt вошла в сечение 1, равна , а масса жидкости, вышедшая за то же время из сечения 2, равна (ρ₁ и ρ₂ - плотность жидкости в сечениях 1 и 2). Так как эти массы должны быть равны, то

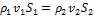
Это уравнение называется уравнением неразрывности. Оно справедливо для движения как жидкости так и для газа. Если рассматривать движение несжимаемой жидкости, плотность которой постоянна, то это уравнение принимает такой вид:

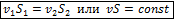
Получается, что в узких сечениях скорость потока больше, чем в широких.

 

Уравнение Бернулли

Рассмотрим узкую трубку тока и два ее сечения 1 и 2. Пусть площади сечений равны S₁ и S₂, а скорости потока в сечениях 1 и 2 равны v₁ и v₂. Рассмотрим очень маленький промежуток времени Δt. За это время жидкость в сечении 1 переместится на расстояние , а в сечении 2 на . Рассмотрим объем жидкости, заключенный между сечениями 1 и 2. Если давление жидкости в сечении 1 равно Р₁, а в сечении 2 – Р₂, то за время Δt силы давления совершают над выделенным объемом работу A (силы давления окружающей жидкости на боковую поверхность трубки тока направлены перпендикулярно поверхности трубка, а значит их работа равна нулю). Эта работа равна изменению энергии выделенного объема жидкости. Но за время Δt слой жидкости толщиной v₁Δt между штриховыми линиями в сечении 1 переместился в слой толщиной v₂Δt в сечении 2. Значит, совершенная силами давления работа равна разности энергий этих двух слоев жидкости:

S1

S2

v1

v2

v1Δt

v2Δt

h2

h1

h=0

Где массы слоев раны и , а h₁ и h₂ – высота сечений 1 и 2 относительно какого-либо нулевого уровня. Таким образом, получаем:

Сокращая на Δt и учитывая, что , получаем:

Это и есть уравнение Бернулли.

Величину можно назвать плотностью кинетической энергии, а величину 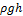- плотностью потенциальной энергии. Тогда можно написать: для стационарного течения идеальной жидкости сумма давления и плотностей кинетической и потенциальной энергий является постоянной для любого сечения потока жидкости.