Теорема: если функция y=f(t) имеет производную в точке t0, функция y=φ(х) имеет производную в точке х0, φ(х0)=t0,то сложная функция y=f(φ(х))= у(х) имеет производную в точке х0, которая находится по формуле f(φ(х))’=(f(φ(x)))t’φ’(x), или в более удобных кратких обозначениях yx’=yt’*tx’ dy/dx=dy/dt*dt/dx. Последняя формула проясняет алгебраический смысл теоремы. Для словесной формулировки теоремы переменную t удобно называть внутренней. Тогда правило дифференцирования сложной функции приобретает вид: производная сложной функции по х равна произведению производной по внутренней переменной на производную внутренней переменной по х.
Док-во: дадим х приращение Δх, тогда t получит приращение Δt=φ(x+Δx)-φ(x), а у, в свою очередь, получит приращение Δy=f(t+Δt)-f(t). Имеем тождество Δy/Δx=Δy/Δt*Δt/Δx. Та limΔx→0 Δy/Δt* Δt/Δx к как функция, имеющая производную, непрерывна, то Δt→0 Δx→0. Из определения производной и теоремы о пределе произведения получаем y’= limΔx→0 Δy/Δx= limΔx→0 Δy/Δt* Δ limΔx→0 Δt/Δx=yt’*tx’. Пример: y=cos2x, y’=2cosx(-sinx)=-sin2x.
18.Обратная функция и её производная. Производные функций y= arcsinx, y=arctgx.
Теорема: пусть функция y=f(х), определенная в некотором интервале, имеет обратную функцию х= f-1(у). тогда если фун-ия y=f(х) имеет произвольную в точке х0 и f’(х0)≠0, то обратная фун-ия имеет производную в точке у0= f(х0), которая равна ху’=1/ ух’ или dx/dy=1/dy/dx
Док-во: пусть Δх- приращение х, соответствующее приращению Δу. Т.к. фун-ия, имеющая производную, непрерывна, а фун-ия, обратная к непрерывной,также непрерывна, тоΔх→0 при Δу→0. Из определения производной и теоремы о пределе частного получаем ху’= limΔу→0 Δх/Δу= limΔx→0 1/Δy/Δх=1/ ух’.
Примеры: 1)у=arcsinx -фун-ия, обратная к фун-ии х= sinу. Поэтому y’x=1/xy’=1/cosy=1/√1-sin2y=1/√1-x2.. аналогично получаем, что (arccosx)’=-1/√1+x2; 2)y=arctgx-фун-ия, обратная к фун-ии x=tgу. Поэтому y’x=1/xy’=1/1/cos2 y=1/1+tg2y=1/1+x2. Аналогично получаем, что (arcctgx)’= -1/1+x2)
19.Производная функции y=In x.Логарифмическое дифференцирование и его применение.
Производная функции y = ln x
Найдём приращение функции 
.
Воспользовавшись непрерывностью логарифмической функции и вторым замечательным пределом, получим 
Для логарифмической функции с произвольным основанием имеем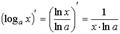 
Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него. Такой прием позволяет эффективно вычислять производные степенных и рациональных функций.
20.Дифференциал функции: определение и формула для вычисления. Эквивалентность дифференцируемости и существования производной.
Дифференциа́л (от лат. — разность, различие) — линейная часть приращения функции. Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х. Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу можно записать так:dy=ƒ'(х)dх,
Выясним теперь связь между дифференцируемостью функции в точке и существованием производной функции в той же точке.
Теорема 1. Для того чтобы функция f была дифференцируемой в некоторой точке x0, необходимо и достаточно, чтобы она имела в этой точке производную; при этом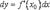 
Доказательство. Необходимость. Пусть функция f дифференцируема в точке x0, т. е. 
. Тогда 
Поэтому производная 
существует и равна A. Отсюда 
Достаточность. Пусть существует производная 
, т. е. существует предел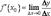 
.Тогда, 
где 
и, следовательно, для 
справедливо равенство 
Теорема Ферма и Ролля.
Теорема Ферма.
Если функция у = f (х), определенная в интервале (а; b), достигает в некоторой точке с этого интервала наибольшего (или наименьшего) значения и существует производная f ′(с), то f ′(с) = 0.
Геометрический смысл этой теоремы состоит в том, что касательная к графику функции у = f (х) в точке с абсциссой с параллельна оси абсцисс.
Теорема Ролля. Если функция у = f (х), непрерывная на отрезке [а; b] и дифференцируемая в интервале (а; b), принимает на концах этого отрезка равные значения f (a) = f (b), то в интервале (а; b) существует такая точка с, что f ′(с) = 0.
Геометрически эта теорема означает следующее: если крайние ординаты кривой у = f (х) равны, то на кривой найдется точка, в которой касательная параллельна оси абсцисс.
22.Теорема Лагранжа и формула конечных приращений. Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка  , что 
Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Механическое истолкование: Пусть f(t) — расстояние точки в момент t от начального положения. Тогда f(b) − f(a) есть путь, пройденный с момента t = a до момента t = b, отношение  — средняя скорость за этот промежуток.
Доказательство
Для функции одной переменной:
|
Введем функцию 
. Для нее выполнены условия теоремы Ролля: на концах отрезка ее значения равны f(a). Воспользовавшись упомянутой теоремой, получим, что существует точка c, в которой производная функции F равна нулю: 
что и требовалось доказать.
